Elastic & Inelastic Collisions (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself

Written by: Katie M

Reviewed by: Caroline Carroll

Elastic collisions

In all collisions and explosions, momentum and energy are always conserved
- However, kinetic energy might not always be
An elastic collision is one in which the kinetic energy is conserved, which means

initial kinetic energy of the system = final kinetic energy of the system

$\sum K_{i} = \sum K_{f}$

However, the final kinetic energy of individual objects in the system may be different from its initial kinetic energy

Some examples of elastic collisions include:
- two hard spheres (e.g. billiard balls) colliding
- bouncing a rubber ball on a surface

Worked Example

A mass $m_{1}$ with initial velocity $v$ collides elastically with a stationary mass $m_{2}$ .

(A) Derive expressions for $v_{1}$ and $v_{2}$ , the final velocities of $m_{1}$ and $m_{2}$ respectively, in terms of $m_{1}$ , $m_{2}$ and $v$ .

(B) For the final velocities of the two masses to be in the same direction, indicate whether $m_{1}$ must be greater than, less than, or equal to $m_{2}$ . Justify your reasoning.

(C) For the final velocities of the two masses to be in opposite directions, indicate whether $m_{1}$ must be greater than, less than, or equal to $m_{2}$ . Justify your reasoning.

Answer:

Part (A)

Step 1: Analyze the scenario

Before the collision, only mass $m_{1}$ is moving, so it will provide the total momentum of the system
After the collision, mass $m_{2}$ will be given a velocity $v_{2}$ and the velocity of mass $m_{1}$ will decrease from $v$ to $v_{1}$
Without knowing the relative sizes of the masses, the direction of $v_{1}$ is unknown

An elastic collision between two masses m1 and m2. Before the collision, mass m1 moves to the right with velocity v, mass m2 is stationary. After the collision, mass m2 moves to the right with velocity v2 and mass m1 has velocity v1 but the direction is unknown.

In an elastic collision, both momentum and kinetic energy are conserved
Therefore, we can write expressions for
- total momentum before = total momentum after
- total kinetic energy before = total kinetic energy after

Step 2: Write expressions for the momentum and kinetic energy of the system

The momentum of the system is

$\sum {\vec{p}}_{i} = \sum {\vec{p}}_{f}$

$m_{1} v = m_{1} v_{1} + m_{2} v_{2}$

The kinetic energy of the system is

$\sum K_{i} = \sum K_{f}$

$\frac{1}{2} m_{1} v^{2} = \frac{1}{2} m_{1} {v_{1}}^{2} + \frac{1}{2} m_{2} {v_{2}}^{2}$

$m_{1} v^{2} = m_{1} {v_{1}}^{2} + m_{2} {v_{2}}^{2}$

Step 3: Rearrange each expression to collect the mass terms and make $v_{1}$ or $v_{2}$ the subject

The momentum expression can be arranged to give

$m_{2} v_{2} = m_{1} v - m_{1} v_{1}$

equation 1: $m_{2} v_{2} = m_{1} (v - v_{1})$

The kinetic energy expression can be arranged to give

$m_{2} {v_{2}}^{2} = m_{1} v^{2} - m_{1} {v_{1}}^{2}$

$m_{2} {v_{2}}^{2} = m_{1} (v^{2} - {v_{1}}^{2})$

equation 2: $m_{2} {v_{2}}^{2} = m_{1} (v + v_{1}) (v - v_{1})$

Step 4: Determine the relationship between the velocities

Divide equation 2 by equation 1, and simplify:

$\frac{m_{2} {v_{2}}^{2}}{m_{2} v_{2}} = \frac{m_{1} (v + v_{1}) (v - v_{1})}{m_{1} (v - v_{1})}$

$v_{2} = v + v_{1}$

Now we have an expression relating the velocities, we can use this along with equation 1 to
- eliminate $v_{2}$ , giving an expression for $v_{1}$ in terms of $m_{1}$ , $m_{2}$ and $v$
- eliminate $v_{1}$ , giving an expression for $v_{2}$ in terms of $m_{1}$ , $m_{2}$ and $v$

Step 5: Write an expression for the final velocity $v_{1}$

Substitute the expression for $v_{2}$ back into equation 1:

$m_{2} (v + v_{1}) = m_{1} (v - v_{1})$

Expand and collect the velocity terms:

$m_{2} v + m_{2} v_{1} = m_{1} v - m_{1} v_{1}$

$v_{1} (m_{1} + m_{2}) = m_{1} v - m_{2} v$

$v_{1} = \frac{m_{1} v - m_{2} v}{m_{1} + m_{2}}$

Step 6: Write an expression for the final velocity $v_{2}$

Substitute the expression for $v_{1}$ into the expression for $v_{2}$ :

$v_{2} = v + v_{1} = v + \frac{m_{1} v - m_{2} v}{m_{1} + m_{2}}$

Combine the fractions, then expand and simplify:

$v_{2} = \frac{v (m_{1} + m_{2})}{m_{1} + m_{2}} + \frac{m_{1} v - m_{2} v}{m_{1} + m_{2}}$

$v_{2} = \frac{m_{1} v + m_{2} v + m_{1} v - m_{2} v}{m_{1} + m_{2}}$

$v_{2} = \frac{2 m_{1} v}{m_{1} + m_{2}}$

Part (B)

Step 1: Analyze the scenario

The expression for $v_{2}$ indicates that it will always have a positive value, as it does not contain any minus signs
The expression for $v_{1}$ indicates it can have a positive or negative value as it does contain a minus sign
Therefore, the final velocities of the two masses will be in the same direction for positive values of $v_{1}$

Step 2: Deduce and justify the relationship

For $v_{1}$ to be in the same direction as $v_{2}$ , $m_{1}$ must be greater than $m_{2}$
Justification:
- From the equation, $v_{1} = \frac{(m_{1} - m_{2}) v}{m_{1} + m_{2}}$ , positive values of $v_{1}$ are possible when $(m_{1} - m_{2}) v > 0$
- This is only possible when $m_{1} > m_{2}$

Part (C)

Step 1: Analyze the scenario

The final velocities of the two masses will be in opposite directions for negative values of $v_{1}$

Step 2: Deduce and justify the relationship

For $v_{1}$ to be in the opposite direction to $v_{2}$ , $m_{1}$ must be less than $m_{2}$
Justification:
- From the equation, $v_{1} = \frac{(m_{1} - m_{2}) v}{m_{1} + m_{2}}$ , negative values of $v_{1}$ are possible when $(m_{1} - m_{2}) v < 0$
- This is only possible when $m_{1} < m_{2}$

Examiner Tips and Tricks

Every AP Physics exam you take will include a question asking you to "derive an expression". Derivations are a key problem-solving skill in physics and serve as a powerful tool for determining relationships and making reliable predictions for numerous scenarios.

If you are finding it tricky to master derivations, try these steps:

Analyze the scenario to identify exactly what is being asked in the derivation and come up with a rough plan for where you want to end up

In the example above, we needed two expressions, one for $v_{1}$ and one for $v_{2}$ in terms of the three quantities given in the question $(m_{1}, m_{2}, v)$ , so it was clear we had to relate the two velocities to each other, and then use algebra to write separate equations for each one.

Begin your solution by identifying one or more fundamental equations from the AP Physics Exam equation sheet

In the example above, we started by applying the fundamental equations for momentum $(p = m v)$ and kinetic energy $(K = \frac{1}{2} m v^{2})$ to each object which gave us two equations as a basis for the rest of the derivation.

Obtain a final expression using the algebraic manipulation skills you know, such as factorizing, expanding, and simplifying variables

In the example above, once we set up the equations containing the required terms, all we had left to do was to rearrange, manipulate, and simplify the expressions algebraically to get them into the required forms

This process should help you to apply a structure to derivations that exam markers can easily follow to ensure you receive maximum credit, but more importantly, you must practice as many of these types of questions as you can to improve your confidence with them.

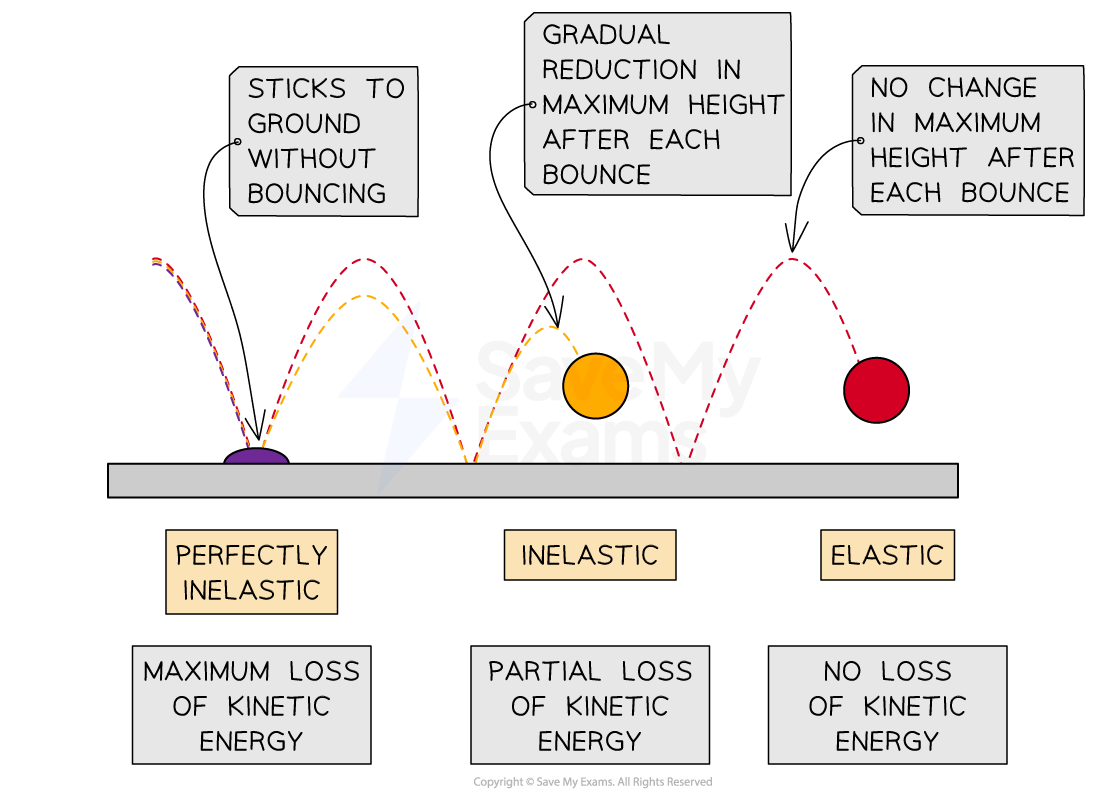
Inelastic collisions

An inelastic collision is one in which the kinetic energy is not conserved, which means

initial kinetic energy of the system > final kinetic energy of the system

$\sum K_{i} > \sum K_{f}$

In other words, the total kinetic energy of the system decreases
This is because some of the initial kinetic energy is transformed into other forms of energy by nonconservative forces

Some examples of inelastic collisions include:
- a bouncing ball which decreases in height with each bounce
- a collision between a car and another object

Perfectly inelastic collisions

A perfectly inelastic collision is a special case in which:
- the maximum amount of kinetic energy is lost to other forms
- the objects stick together and move with the same velocity after the collision
Some examples of perfectly inelastic collisions include:
- two lumps of clay sticking together after colliding
- a ballistic pendulum i.e. a bullet becoming embedded in a wooden block

Comparison of elastic and inelastic collisions

Diagram showing 3 types of collision: perfectly inelastic (maximum kinetic energy loss), inelastic (partial kinetic energy loss), and elastic (no kinetic energy loss). — Momentum is conserved in all collisions, but kinetic energy is not. In elastic collisions, there is no loss of kinetic energy, whereas a perfectly inelastic collision is characterized by a maximum loss of kinetic energy

Worked Example

A car of mass $m$ , traveling with a velocity $v_{0}$ , strikes a stationary vehicle of mass $2 m$ in a head-on inelastic collision and the bumpers lock together.

What fraction of the initial kinetic energy is lost in this collision?

A $\frac{1}{2}$

B $\frac{1}{3}$

C $\frac{1}{4}$

D $\frac{2}{3}$

The correct answer is D

Answer:

Step 1: Analyze the scenario

Before the collision, only the car of mass $m$ is moving, so it will provide the total momentum of the system
After the collision, the cars become one object of total mass $3 m$ and velocity $v$
This is an example of a perfectly inelastic collision

Two blocks before and after a collision. Before: Block of mass m moves with velocity v0 and collides with a stationary block of mass 2m. After: Both blocks move together with velocity v.

Step 2: Use conservation of momentum to relate the velocities

Conservation of momentum: the total momentum before the collision is equal to the total momentum after

$\sum {\vec{p}}_{i} = \sum {\vec{p}}_{f}$

$m v_{0} = 3 m v$

$v_{0} = 3 v$

Step 3: Determine the initial and final kinetic energies

The initial kinetic energy of the system is:

$K_{i} = \frac{1}{2} m {v_{0}}^{2} = \frac{1}{2} m {(3 v)}^{2} = \frac{9}{2} m v^{2}$

The final kinetic energy of the system is:

$K_{f} = \frac{3}{2} m v^{2}$

Step 4: Determine the fraction of kinetic energy lost

The change in kinetic energy is equal to:

$∆ K = K_{i} - K_{f}$

$∆ K = \frac{9}{2} m v^{2} - \frac{3}{2} m v^{2}$

$∆ K = 3 m v^{2}$

The fraction of kinetic energy lost is therefore:

$\frac{∆ K}{K_{i}} = \frac{3 m v^{2}}{\frac{9}{2} m v^{2}} = \frac{2}{3}$

Therefore, the correct option is D

Examiner Tips and Tricks

It can be helpful to think about collisions and explosions as if there are four types rather than two:

elastic - kinetic energy conserved
perfectly elastic - kinetic energy conserved and no energy transferred between objects
inelastic - kinetic energy not conserved
perfectly inelastic - kinetic energy not conserved and maximum energy transferred to surroundings

However, in AP Physics 1, be aware that the 'perfectly elastic' collision type will not be tested.

Last updated: 27 September 2024

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself

Did this page help you?

Previous:Momentum in ExplosionsNext:Rotating Systems

Elastic & Inelastic Collisions (College Board AP® Physics 1: Algebra-Based)

Study Guide

Elastic collisions

Worked Example

Examiner Tips and Tricks

Inelastic collisions

Perfectly inelastic collisions

Comparison of elastic and inelastic collisions

Worked Example

Examiner Tips and Tricks

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Katie M

Author: Caroline Carroll