Vectors & Motion in Two Dimensions (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself

Author

Leander Oates

Expertise

Physics

Analyzing motion in two dimensions

The same kinematic equations can be used to analyze motion in two dimensions
- The individual equations are covered in more detail in the study guide Kinematic equations
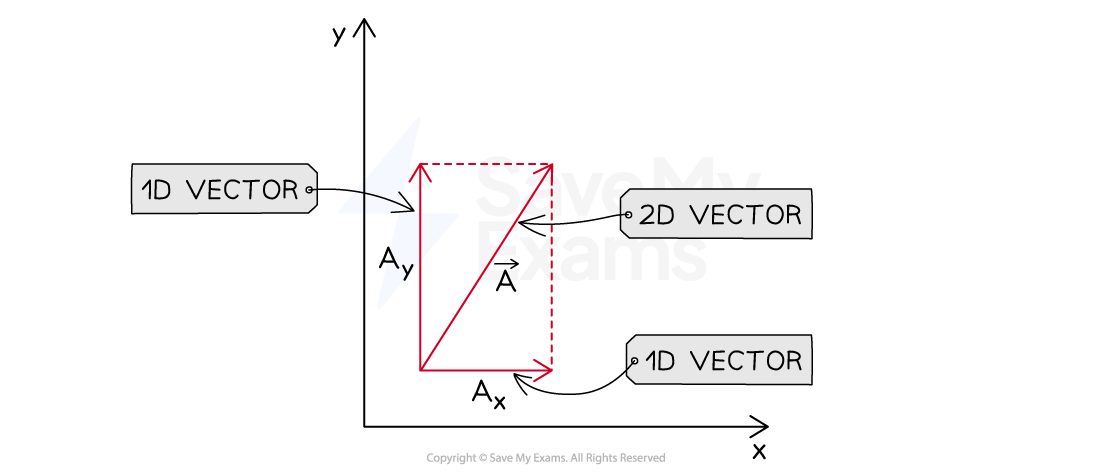
Two-dimensional motion can be separated into one-dimensional components
- The kinematic equations can be used on each component

Diagram of a two-dimensional vector A with components Ax and Ay. The vector forms a right triangle with these components on an x-y coordinate plane. Labels identify 1D and 2D vectors. — **Two-dimensional vectors can be split into component vectors**

Worked Example

A carrier jet is an aircraft that takes off from a large boat called an aircraft carrier. The jet is catapulted from the aircraft carrier to reach the velocity required for takeoff on such a short runway.

At the moment of takeoff, a jet has a horizontal acceleration of $25 m / s^{2}$ and a vertical acceleration of $11 m / s^{2}$ . The jet's initial velocity is $64 m / s$ in the horizontal direction and $19 m / s$ in the vertical direction.

Calculate the resultant final velocity of the jet after $7 s$ .

Answer:

Step 1: Analyze the scenario

To find the resultant final velocity, the component final velocities must first be calculated

Step 2: List the known quantities

Taking forward and upward to be positive

Horizontal acceleration, $a_{x} = 25 m / s^{2}$
Horizontal initial velocity, $v_{x 0} = 64 m / s$
Vertical acceleration, $a_{y} = 11 m / s^{2}$
Vertical initial velocity, $v_{y 0} = 19 m / s$
Time interval, $t = 7 s$

Step 3: Select a suitable kinematic equation to calculate the final velocity components

Displacement is not required

$v_{x} = v_{x 0} + a_{x} t$

$v_{x} = 64 + (25 \cdot 7) = 239 m / s$

$v_{y} = 19 + (11 \cdot 7) = 96 m / s$

Step 4: Calculate the magnitude of the resultant final velocity

$v_{x + y} = \sqrt{239^{2} + 96^{2}} = 258 m / s$

Step 5: Calculate the direction of the resultant final velocity

$v_{x + y} = \tan^{- 1} (\frac{v_{y}}{v_{x}})$

$v_{x + y} = \tan^{- 1} (\frac{96}{239}) = 22 °$ from the horizontal

Step 6: State the resultant final velocity

$v_{x + y} = 258 m / s at 22 ° to the horizontal$

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Next topic

Did this page help you?