Projectile Motion (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself

Author

Leander Oates

Expertise

Physics

Projectile motion

Projectile motion is a special case of two-dimensional motion

Projectile motion will always have:
- zero acceleration in one dimension
- constant, nonzero acceleration in the second dimension

A projectile is defined as:

An object moving freely under gravity in a two dimensional plane

Examples of projectiles include:
- throwing a ball
- jumping off a diving board
- hitting a baseball with a bat
Projectiles are usually launched or thrown into the air, at which point the only force acting on the object is the force of weight
- It is assumed air resistance is ignored
Therefore, the constant nonzero acceleration in the second dimension is acceleration due to gravity at the Earth's surface, $g = 10 m / s^{2}$

Calculations involving projectile motion

The vertical and horizontal components of motion are independent of one another
- Each plane of motion must be evaluated separately using the kinematic equations
A projectile will have a parabolic trajectory if it is launched at any angle other than directly vertical
The direction of the resultant velocity of a projectile is an angle, θ , to the horizontal
- The magnitude of the component velocities can be calculated using trigonometry

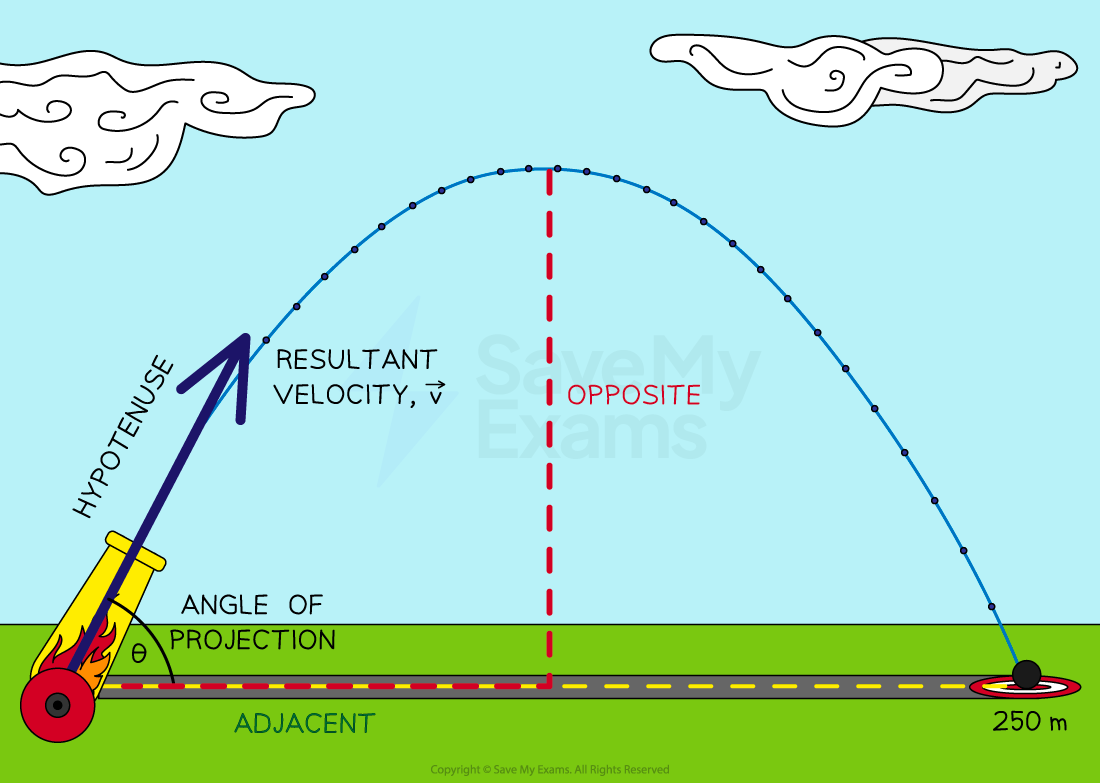
Diagram of a cannonball's projectile motion, showing angle of projection, resultant velocity, hypotenuse, opposite, and adjacent sides. — **An object in a projectile motion trajectory has a resultant velocity at a given angle to the horizontal ground**

Some key terms to know:
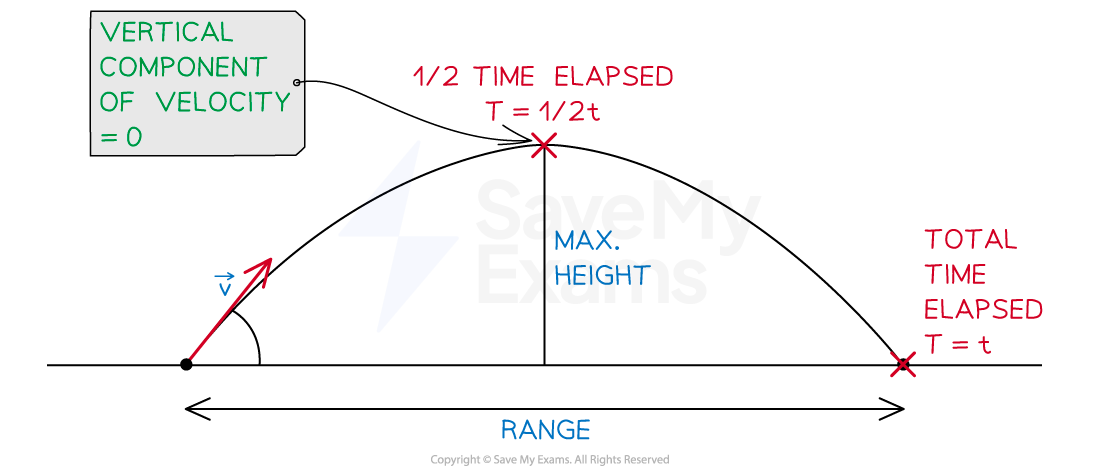
- Time of flight (total time): how long the projectile is in the air
  - For typical projectile motion, the time to the maximum height is half of the total time
- Maximum height attained: the height at which the projectile is momentarily at rest
  - This occurs when the vertical velocity component is equal to zero
  - The projectile is at its maximum height when half of its total time has elapsed
- Range: the horizontal displacement of the projectile

Diagram showing projectile motion with labels for total range (R), initial velocity (u), maximum height (H), and time elapsed. Vertical velocity is 0 at max height. — **An object in projectile motion will have a vertical velocity of zero at maximum height when half the time has elapsed**

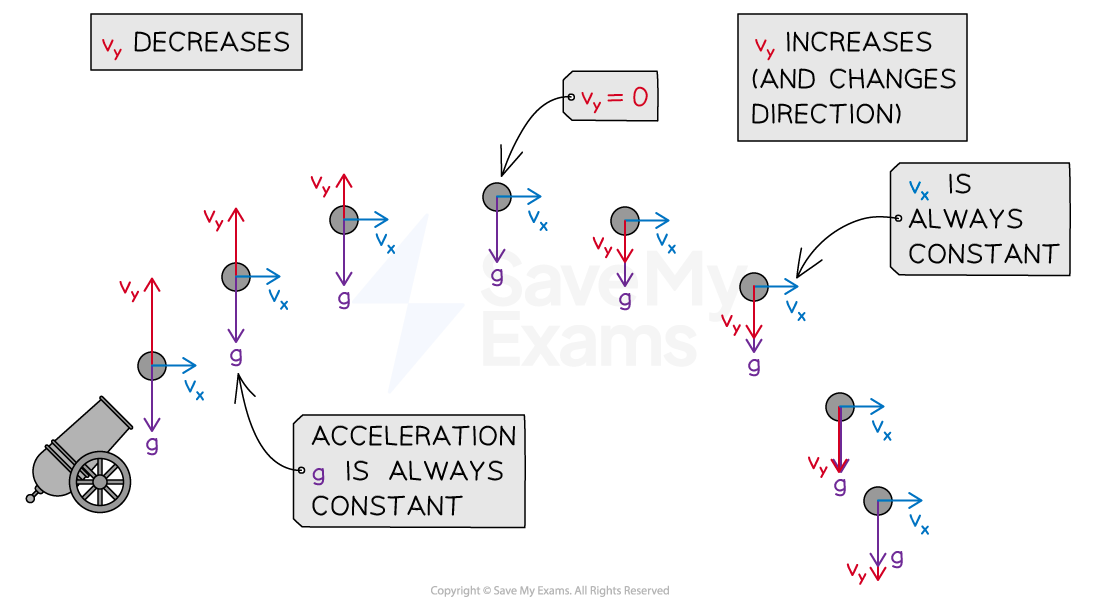
For objects in projectile motion:
- The horizontal velocity is constant
- Therefore, the horizontal acceleration is zero
- The vertical velocity changes
- The vertical acceleration is constant at $10 m / s^{2}$ downward

A diagram showing projectile motion with a cannon firing a ball. It illustrates decreasing and increasing vertical velocity (Vy), constant horizontal velocity (Vx), and constant acceleration (g). — **Acceleration and horizontal velocity are always constant whilst vertical velocity changes**

Worked Example

A soccer ball at rest on the ground, is kicked with an initial velocity of $12 m / s$ at an angle of $35 °$ relative to the ground.

Considering the two-dimensional motion of the soccer ball, calculate:

(a) the time of flight.

(b) the maximum height attained.

Answer:

Analyze the scenario

Time of flight is the total time that the ball is in the air
The ball reaches its maximum height when its vertical velocity drops to zero
Maximum height occurs halfway through its time of flight
The range is determined by the horizontal displacement during the time of flight

Part (a) Calculate the time of flight

Step 1: List the known quantities

Taking upward as positive
Magnitude of resultant initial velocity, $v_{0} = 12 m / s$
Direction of initial velocity, $θ_{0} = 35 °$
Acceleration, $g = - 10 m / s^{2}$

Step 2: Consider the y direction

The $y$ component of the initial velocity, $v_{y 0}$ , is given by:

$v_{y 0} = v_{0} (\sin θ)$

$v_{y 0} = 12 \cdot \sin (35)$

At the apex of the projectile motion, the vertical velocity is momentarily zero as it turns from travelling upwards to downwards
- Use this moment as final velocity in the $y$ direction, $v_{y} = 0$

Step 3: Apply the correct kinematic equation

To find the time taken to reach the apex, use the equation:

$v_{y} = v_{y 0} + a_{y} t$

$0 = 12 \cdot \sin (35) - g t$

$g t = 12 \cdot \sin (35)$

$t = \frac{12}{g} \sin (35)$

The time taken to reach the apex of motion is half the total time
- This is because the motion is symmetrical
Total time of flight is therefore:

$t_{t o t a l} = 2 \cdot \frac{12}{10} \sin (35)$

$t_{t o t a l} = 1.38 s$

Part (b) Calculate the maximum height

Step 1: List the known quantities

Initial vertical velocity, $v_{y 0} = 12 \sin (35)$
Final vertical velocity at apex, $v_{y} = 0 m / s$
Acceleration, $g = - 10 m / s^{2}$
Total time of flight is known, but it is best to use quantities given in the question

Step 2: Apply the correct fundamental equation

To find the displacement at the apex of the trajectory, $h$ , use the following equation and set the initial displacement, $y_{0}$ , to zero:

${v_{y}}^{2} = v_{y 0}^{2} + 2 a_{y} (y - y_{0})$

$h = y - y_{0}$

$0 = {(12 \cdot \sin (35))}^{2} - 2 g h$

Rearrange for $h$ and substitute known quantities:

$h = \frac{{(12 \sin (35))}^{2}}{2 \cdot 10}$

$h = 2.37 m$

Part (c) Calculate the range

Step 1: List the known quantities

Magnitude of resultant initial velocity, $v_{0} = 12 m / s$
Direction of initial velocity, $θ_{0} = 35 °$
Total time of flight, $t_{t o t a l} = 1.38 s$

Step 2: Consider the horizontal direction

In the $x$ direction, no forces act so acceleration is zero
The initial $x$ component of velocity is given by:

$v_{x 0} = 12 \cdot \cos (35)$

The soccer ball continues at this horizontal velocity for the duration of the motion

Step 3: Apply the correct kinematic equation

To find the horizontal range, $R$ , use the equation:

$x = x_{0} + v_{x 0} t + \frac{1}{2} a_{x} t^{2}$

Acceleration is zero because horizontal velocity is always constant
Total time is the same as that of the vertical motion:

$x - x_{0} = R = 12 \cdot \cos (35) t_{t o t a l} + 0$

$R = 12 \cdot \cos (35) (1.38)$

$R = 13.6 m$

Examiner Tip

The trick to these calculations is setting the relevant velocities to zero. Practice with these techniques prior to your exam.

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Next topic

Did this page help you?

Projectile Motion (College Board AP® Physics 1: Algebra-Based)

Study Guide

Projectile motion

Calculations involving projectile motion

Worked Example

Examiner Tip

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Leander Oates