Scalar & Vector Quantities (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself

Written by: Leander Oates

Reviewed by: Caroline Carroll

Scalar & vector quantities

Some physical quantities in math and physics are scalar quantities and some are vector quantities
Scalar quantities have only magnitude (no direction)
Vector quantities have both magnitude and direction
- For example, 10 m/s is a scalar quantity, and 10 m/s north is a vector quantity
Vectors can be visually modeled using arrows
- The length of the arrow represents the magnitude of the vector
- The direction of the arrow represents the direction of the vector
- The length of the arrows must be proportional their magnitudes

Three horizontal arrows labeled "v" (5 m/s EAST), "2v" (10 m/s EAST), and "3v" (15 m/s EAST), showing increasing speeds to the right. — The lengths of vector arrows are proportional to their magnitudes. The 10 m/s vector arrow is twice as long as the 5 m/s vector arrow, and the 15 m/s vector arrow is three times as long as the 5 m/s arrow.

Examples of scalar and vector quantities

The table below lists some examples of scalar and vector quantities
Corresponding scalar and vector quantities are aligned where applicable

Table of scalar and vector quantities

Scalar	Vector
	position
distance	displacement
speed	velocity
	acceleration
mass	weight
	force
	momentum
energy
temperature
power

Distance and displacement

Distance is a measure of how far an object travels
Distance is a scalar quantity with a magnitude but not a direction
For example, an athlete runs a 300 m race on a 400 m track; the distance traveled by the athlete is 300 m

Distance traveled on a race track

A 300-meter race on a 400 m track, showing the "Start" point on the left and the "Finish" point on the right, with arrows indicating the running direction. — **The total distance traveled by the athlete is 300 m**

Displacement is a measure of the change in an object's position
Displacement is a vector quantity with both magnitude and direction
For example, the athlete's displacement is 100 m to the right

Distance and displacement on a race track

A 300-meter race on a 400 m track with arrows showing the distance traveled around the track as 300 m, but the displacement is 100 m to the right of their starting position — **Although the athlete has run a distance of 300 m, their change in position, or displacement, is 100 m to the right of where they started**

Another example is a person hiking in the woods who marks out their route on a map
The distance traveled is the path they walked
Their displacement is a straight line arrow drawn from their starting position to their finishing position (so this includes their direction)

Distance and displacement of a hiker

A depiction of a map showing the route taken by the hiker through the woods. The straight line from Start to Finish is displacement, while the curved path represents distance. — **The distance traveled is the dotted line, this is the route they walked. Their displacement is a straight line showing the change in position between their starting point and their finishing point**

Speed and velocity

Speed is the distance traveled per unit time
Speed is a scalar quantity with a magnitude only
Velocity is the rate of change of displacement
Velocity is a vector quantity with both magnitude and direction
- In other words, velocity is speed in a given direction

Mass and weight

Mass is a measure of the amount of matter in an object
Mass is a scalar quantity with a magnitude only
Weight is the gravitational force exerted on an object with mass when placed in a gravitational field
Force is a vector quantity with both magnitude and direction

Examiner Tips and Tricks

Forces as vectors are covered in more detail in the study guide on Free-body diagrams

Vector notation

Vectors are given a specific notion with an arrow above the symbol for the given quantity

$\vec{v} = {\vec{v}}_{0} + \vec{a} t$

Where:
- $\vec{v}$ = velocity, measured in $m / s$
- ${\vec{v}}_{0}$ = initial velocity, measured in $m / s$
- $\vec{a}$ = acceleration, measured in $m / s^{2}$
- $t$ = time, measured in $s$
The magnitude of a vector quantity is represented by parallel lines at either side of the symbol

$|\vec{v}| = |{\vec{v}}_{0}| + |\vec{a}| t$

Where:
- $|\vec{v}|$ = the magnitude of the velocity, measured in $m / s$
- $|{\vec{v}}_{0}|$ = the magnitude of the initial velocity, measured in $m / s$
- $|\vec{a}|$ = the magnitude of the acceleration, measured in $m / s^{2}$
- $t$ = time, measured in $s$

Examiner Tips and Tricks

You may see different types of vector notation in textbooks. Vectors can be represented in the following ways:

$A$ , $A$ , $\bar{A}$ , $\overset{⇀}{A}$ or $\vec{A}$

In your exam, it is always best to stick with the notation used by the College Board, which is $\vec{A}$ as shown on the equation sheet.

When not to use vector notation

For vectors in one dimension, the positive or negative value represents the direction

One-dimensional vectors. Arrow labeled -2v points left; arrow labeled 3v points right. Caption explains negative value shows opposite direction to positive. — **For vectors in one dimension, vector notation is not required. The positive and negative values represent the direction**

When vectors are presented along an axis, the axis provides the direction

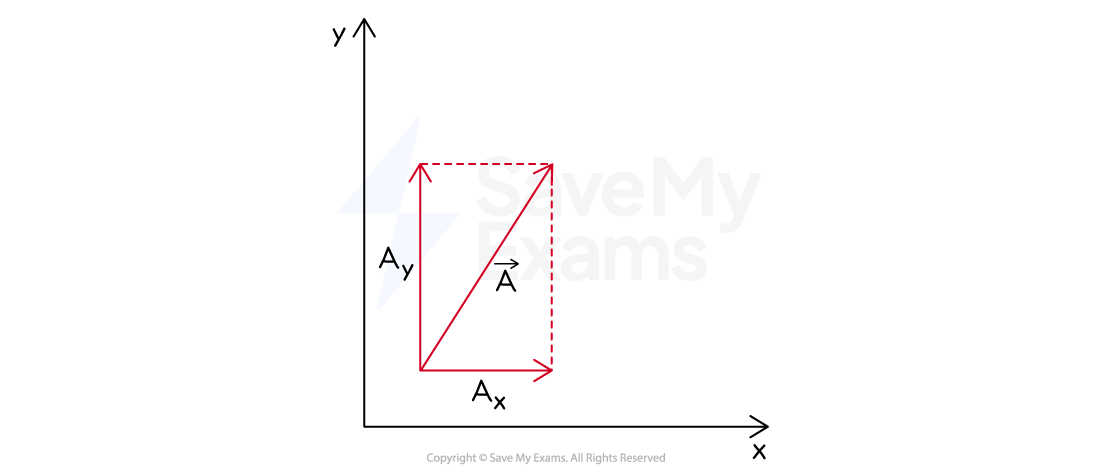
A 2D graph with x and y axes, showing a vector decomposed into its x and y components, forming a right triangle with dashed lines. — **When vectors are presented on axes, vector notation is not required. The axes provide the direction**

Likewise, when the axes are presented in algebraic form, vector notation is not required

$v_{x} = v_{x 0} + a_{x} t$

Where:
- $v_{x}$ = velocity in the $x$ direction, measured in $m / s$
- $v_{x 0}$ = initial velocity in the $x$ direction, measured in $m / s$
- $a_{x}$ = acceleration in the $x$ direction, measured in $m / s^{2}$
- $t$ = time, measured in $s$

Derived equation

In one dimension, the sign of a component completely describes the direction of an object
For example, in the following equation, the direction is either positive or negative along the $x$ -axis

$v_{x} = v_{x 0} + a_{x} t$

Step 1: Identify the fundamental principle

Vector components are indicated with arrows above the vector quantities, such as in the following equation:

$\vec{v} = {\vec{v}}_{0} + \vec{a} t$

Step 2: Apply the specific conditions

In the $x$ direction, the vector components become:
- $\vec{v} \Rightarrow v_{x}$
- ${\vec{v}}_{0} \Rightarrow v_{x 0}$
- $\vec{a} \Rightarrow a_{x}$
Therefore, the equation in terms of the motion along the $x$ axis becomes:

$v_{x} = v_{x 0} + a_{x} t$

Examiner Tips and Tricks

You will be asked to derive an equation in the exam. Always start by identifying the fundamental principle, which may be a fundamental law, a relationship, or an equation. Then apply the fundamental principle to the situation using logical reasoning. It is a good idea to use words to briefly outline your process so that the examiner can follow your logic. The examiner can only award marks if they understand your process.

Last updated: 10 October 2024

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself

Did this page help you?

Next:Combining Vectors

Scalar & Vector Quantities (College Board AP® Physics 1: Algebra-Based)

Study Guide

Scalar & vector quantities

Examples of scalar and vector quantities

Table of scalar and vector quantities

Distance and displacement

Distance traveled on a race track

Distance and displacement on a race track

Distance and displacement of a hiker

Speed and velocity

Mass and weight

Examiner Tips and Tricks

Vector notation

Examiner Tips and Tricks

When not to use vector notation

Derived equation

Examiner Tips and Tricks

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Leander Oates

Author: Caroline Carroll