Combining Vectors (College Board AP® Physics 1: Algebra-Based)

Study Guide

Written by: Leander Oates

Reviewed by: Caroline Carroll

Combining vectors

Vector sums in one dimension

In one-dimensional coordinate systems, vectors of opposing directions are represented as positive and negative

Two pairs of vectors labeled A and -A, B and -B, showing equal magnitudes with opposing directions. Text below reads "Vectors of equal magnitude with opposing directions." — Vectors A and -A are equal in magnitude but opposite in direction. Vectors B and -B are equal in magnitude and opposite in direction. Vectors B and -B are smaller in magnitude than vectors A and -A, and have a different direction.

Scalar multiplication

Vectors can be multiplied by a scalar
The effect is either a change in magnitude or a reversal of the direction
For example, vector $\vec{B}$ is multiplied by $2$
- $\vec{B}$ is the vector
- $2$ is the scalar
The resultant vector is $2 \vec{B}$
- The magnitude of the vector has doubled
- The direction has not changed

Vector B and its scalar multiple 2B, with B represented by a shorter arrow and 2B by a longer arrow to indicate increased magnitude. — **When the vector B is multiplied by the scalar 2, the magnitude of the vector doubles but the direction stays the same**

When vector $\vec{B}$ is multiplied by $- 1$
- $\vec{B}$ is the vector
- $- 1$ is the scalar
The resultant vector is $- \vec{B}$
- The magnitude of the vector has not changed
- The direction has reversed

Diagram showing vector B pointing right and negative vector B pointing left, with text below stating "SCALAR MULTIPLICATION RESULTING IN A REVERSE OF DIRECTION". — **When the vector B is multiplied by the scalar -1, the magnitude of the vector stays the same, but the direction reverses**

Vector addition

Vectors can be added together using a vector sum
The effect is a resultant vector that describes the combined effect of both vectors
For example, vector $\vec{A}$ is added to vector $\vec{B}$
The resultant vector is $\vec{A} + \vec{B}$

$\vec{A} + \vec{B} = \vec{A} + \vec{B}$

There are two methods to adding vectors graphically:
- The tip-to-tail method
- The parallelogram method

Tip-to-tail method of adding vectors

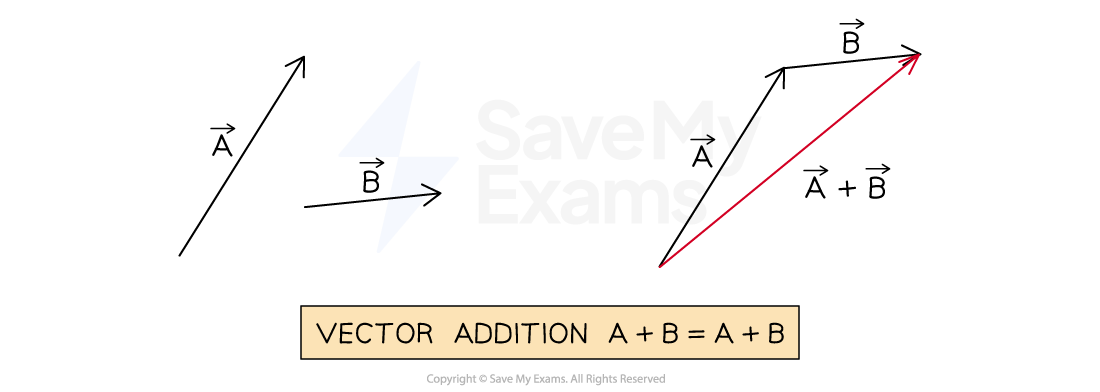
Diagram illustrating vector addition: Vector A and Vector B are shown individually and then added together, forming Vector A + B. Text below reads "VECTOR ADDITION: A + B = A + B" — **Vector A and vector B are added together, the resultant vector is A + B**

The tip-to-tail method places the vector arrows tip-to-tail to find the resultant vector

Parallelogram method of adding vectors

Vector addition using the parallelogram method. Two vectors A and B form a parallelogram, with the resultant vector A+B shown in red. — **The parallelogram method gives the same resultant vector A + B. Notice that the dotted line for vector B is positioned in the exact same way as the tip to tail method**

The parallelogram method places the vectors tail-to-tail to find the resultant vector

Vector subtraction

Vectors can also be subtracted using a vector sum and scalar multiplication
For example, vector $\vec{B}$ is subtracted from vector $\vec{A}$
Vector $\vec{B}$ is first multiplied by the scalar $- 1$
- This reverses the direction of vector $\vec{B}$ to give $- \vec{B}$
The vectors are then added by placing them tip to tail
The resultant vector is $\vec{A} + (- \vec{B})$

$\vec{A} - \vec{B} = \vec{A} + (- \vec{B})$

Diagram illustrating vector subtraction. Vector A and B are shown separately. On the right, vector A and negative B combine to form resultant vector A + (-B). — **Vector B is subtracted from vector A by using scalar multiplication to reverse the direction of B and using vector addition by placing vectors A and -B tip to tail**

Vectors in one and two dimensions

A one-dimensional vector has magnitude and direction along a single straight line
- This can be along the $x$ -axis or $y$ -axis in a coordinate system
A two-dimensional vector has magnitude and direction in a plane
- This means it has two component vectors: one along the $x$ -axis and one along the $y$ -axis

Resolving vectors in two dimensions

Two-dimensional vectors can be resolved into two perpendicular one-dimensional vectors
- The vector along the horizontal $x$ -axis
- The vector along the vertical $y$ -axis
These are called component vectors

Graph depicting a 2D vector A with components Ax and Ay. Ax and Ay are 1D vectors along x and y axes respectively. Direction of A indicated by arrows. — **Two-dimensional vectors can be resolved into their component vectors along the x and y axes**

Finding the magnitude of the vector

The magnitude of a two-dimensional vector can be found using Pythagoras' theorem

$a^{2} + b^{2} = c^{2}$

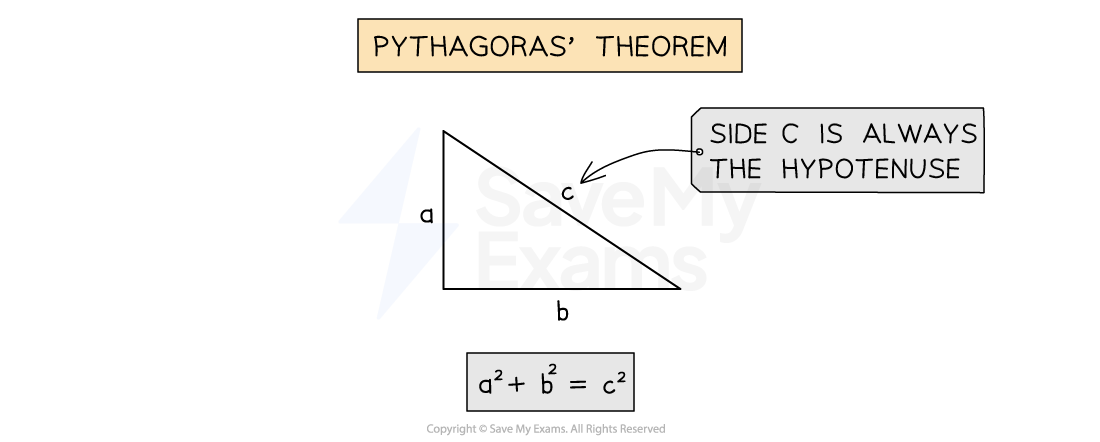
The two-dimensional vector is the hypotenuse of the triangle, therefore:

${(\vec{A})}^{2} = {({\vec{A}}_{y})}^{2} + {({\vec{A}}_{x})}^{2}$

$\vec{A} = \sqrt{{(A_{y})}^{2} + {(A_{x})}^{2}}$

Finding the direction of the vector

The direction of the vector can be described with respect to an axis
- This is usually the horizontal $x$ -axis, unless otherwise directed
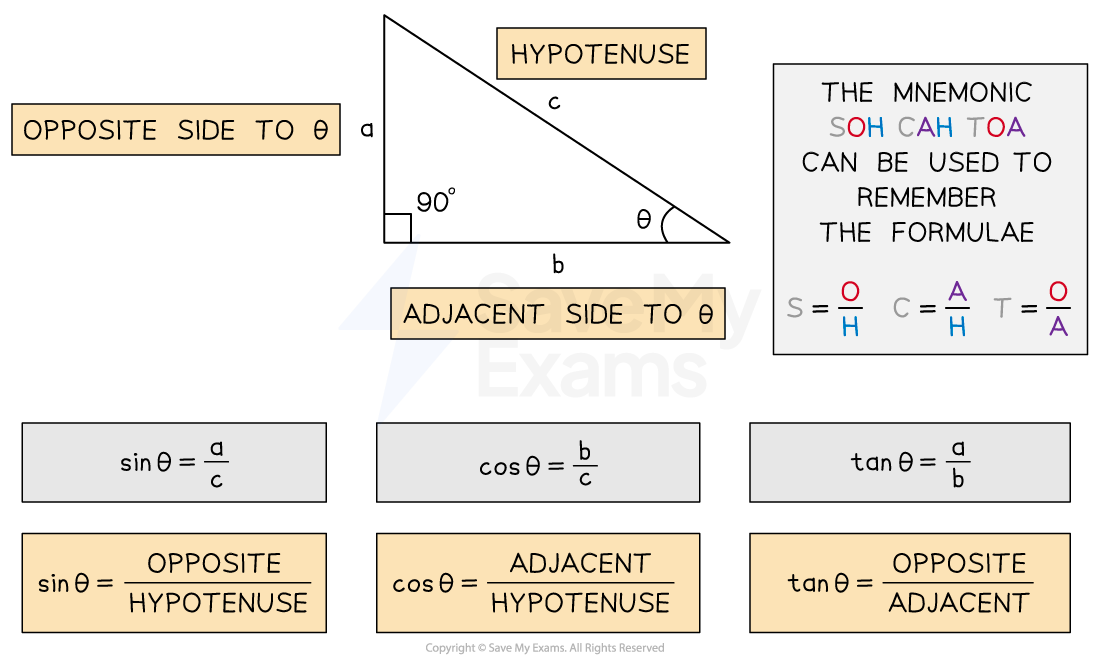
The symbol theta $θ$ is used for an unknown angle

A vector diagram showing vector A with components Ax and Ay, making an angle theta with the x-axis. Text indicates the angle is measured from the x-axis. — **The angle is generally measured from the x-axis unless otherwise stated**

Trigonometry can then be used to find:
- the angle, if the magnitude of the vectors are known
- the magnitude of a vector, if the angle and the magnitude of one vector are known

Diagram of a right triangle with sides a, b, and hypotenuse c. Includes trigonometric ratios: sin θ = a/c, cos θ = b/c, tan θ = a/b, and mnemonic SOHCAHTOA. — **Trigonometry is used for calculating an angle in a right angled triangle**

Worked Example

A kayaker rows from the north bank to the south bank of a river flowing due east at speed $r$ . The kayaker knows they can maintain an average speed of $k$ when rowing in still water.

(a) State an equation relating the velocities $k$ and $r$ .

(b) Give an expression for the direction of the kayaker as they cross the river in terms of $k$ and $r$ .

(c) Before the kayaker sets off, the river flow slows to half its initial speed. Derive an equation for the new velocity that the kayaker needs to cross the river.

Answer:

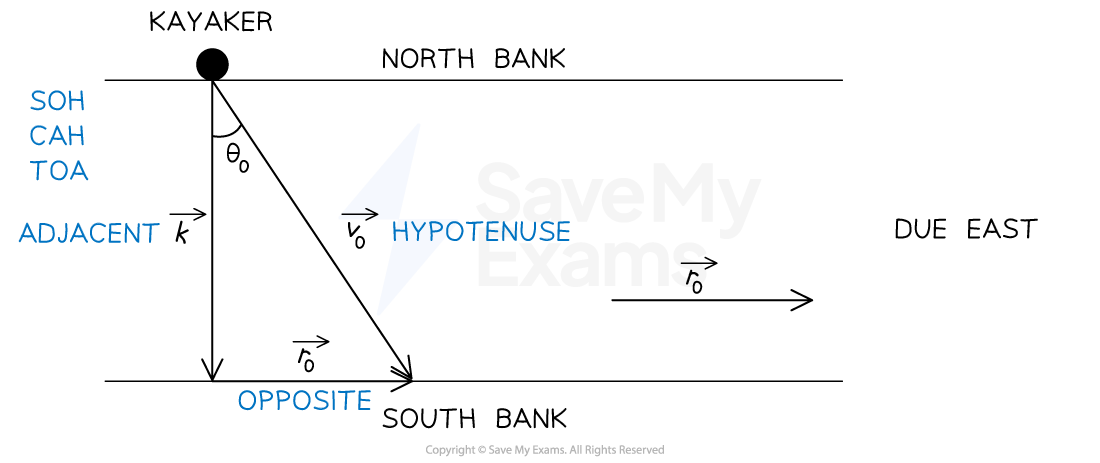
Analyze the scenario

Sketch a diagram to help visualize the situation

Diagram showing a kayaker on the North Bank aiming for the South Bank with velocity vector v0 at an angle θ0. Additional vectors k, r0, and r direction are labeled.

The kayaker travels from the north bank to the south bank, therefore:
- The kayaker is positioned on the north bank
- The kayaker travels south across the river
The kayaker can maintain a speed of $k$ in still water, therefore:
- The kayaker's velocity in still water can be written as $\vec{k}$ to the south
The river flows due east at an initial speed of $r$ , therefore:
- The initial velocity of the river can be written as ${\vec{r}}_{0}$ to the east
The kayaker will be pulled to the east by the current, therefore:
- The initial resultant velocity of the kayaker can be written as ${\vec{v}}_{0}$ at angle $θ_{0}$ east from south

Part (a)

State an equation relating the velocities $k$ and $r$

Step 1: Identify the relevant fundamental principle

The initial velocity vectors $\vec{k}$ and ${\vec{r}}_{0}$ are the components of vector ${\vec{v}}_{0}$
Therefore, the relevant fundamental principle is vector addition

Step 2: Apply the fundamental principle to the scenario

The sum of vectors $\vec{k}$ and ${\vec{r}}_{0}$ is equal to the resultant vector ${\vec{v}}_{0}$

${\vec{v}}_{0} = k + {\vec{r}}_{0}$

Part (b)

Give an expression for the direction of the kayaker as they cross the river in terms of $k$ and $r$

Step 1: Identify the direction of the resultant vector ${\vec{v}}_{0}$

The direction of a resultant vector is described by an angle
The value of the initial angle is unknown, so it can be written as $θ_{0}$

Step 2: Determine the trigonometric ratio for the resultant vector ${\vec{v}}_{0}$

Diagram of a kayaker paddling from the north bank to the south bank forming a right triangle. Labels include SOH CAH TOA, adjacent, opposite, hypotenuse, theta0, and vectors.

Use the mnemonic SOH CAH TOA to recall the trigonometric ratios
Choose the ratio that includes the terms of $\vec{k}$ and ${\vec{r}}_{0}$
- $\vec{k}$ is the side adjacent to the angle $θ_{0}$
- ${\vec{r}}_{0}$ is the side opposite to the angle $θ_{0}$
- Therefore, the correct trigonometric ratio is tangent

$θ_{0} = \tan^{- 1} (\frac{{\vec{r}}_{0}}{\vec{k}})$

Part (c)

Before the kayaker sets off, the river flow slows to half its initial speed. Derive an equation for the new velocity that the kayaker needs to cross the river

Step 1: Add the information to the sketch

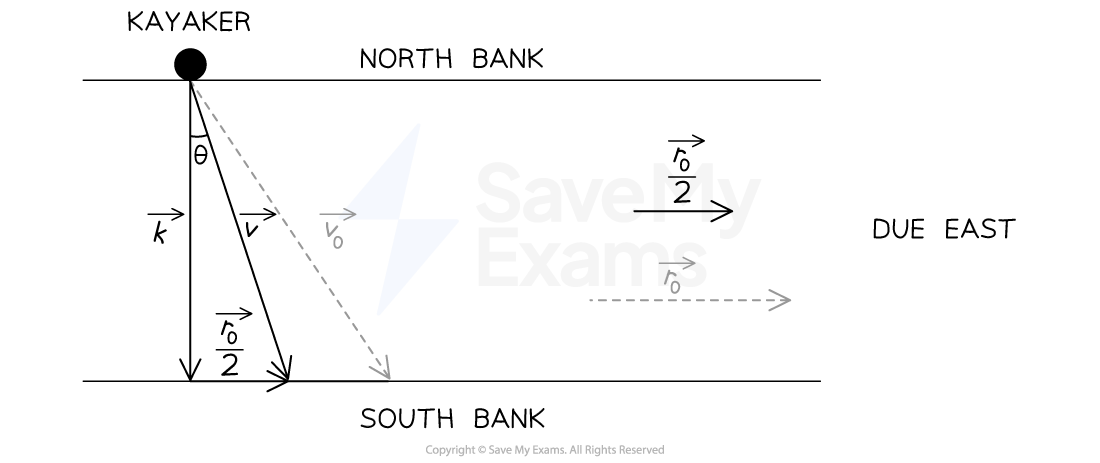
Diagram of a kayaker paddling from the north bank to the south bank. Various labeled vectors illustrate the kayaker's velocity, direction, and distance traveled.

Step 2: Determine an expression for the new river speed vector

The initial velocity vector for river speed is ${\vec{r}}_{0}$ east
The new river speed is half of the initial speed
Therefore, the new velocity of the river can be written as $\frac{\vec{r_{0}}}{2}$

Step 3: Determine the magnitude of the new resultant vector

The new resultant velocity vector can be written as $\vec{v}$
The magnitude of this vector is the sum of the vectors $\vec{k}$ and $\frac{{\vec{r}}_{0}}{2}$

$\vec{v} = k + \frac{{\vec{r}}_{0}}{2}$

Step 4: Determine the direction of the new resultant vector

The direction of the new resultant vector is the new angle, which can be written as $θ$
The expression for the initial direction from part (B) can be applied to the new situation

$θ = \tan^{- 1} (\frac{{\vec{r}}_{0}}{2} \cdot \frac{1}{\vec{k}})$

$θ = \tan^{- 1} (\frac{{\vec{r}}_{0}}{2 k})$

Step 5: State the magnitude and direction of the new resultant vector

$\vec{v} = k + \frac{{\vec{r}}_{0}}{2}$ at an angle $θ = \tan^{- 1} (\frac{{\vec{r}}_{0}}{2 \vec{k}})$ east from south

Examiner Tips and Tricks

The problem above is an example of the Qualitative/Quantitative Translation style of free-response question. This is where you are expected to make and justify a claim about a scenario, derive an equation related to the scenario, and then use consistent reasoning to formulate your answer.

You are expected to use algebra as a mode of communication, but it is always a good idea to also use worded statements to show the examiner your thought process. The examiner can only award marks where your logic is clear enough for them to follow. For this reason, it is always a good idea to read through your answer and check for clarity, adding in any notes that you think it needs.

Last updated: 18 October 2024

You've read 0 of your 5 free study guides this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself

Did this page help you?

Previous:Scalar & Vector QuantitiesNext:Displacement

Combining Vectors (College Board AP® Physics 1: Algebra-Based)

Study Guide

Combining vectors

Vector sums in one dimension

Scalar multiplication

Vector addition

Tip-to-tail method of adding vectors

Parallelogram method of adding vectors

Vector subtraction

Vectors in one and two dimensions

Resolving vectors in two dimensions

Finding the magnitude of the vector

Finding the direction of the vector

You've read 0 of your 5 free study guides this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

Unit 1: Kinematics

Scalars & Vectors

Scalar & Vector Quantities

Combining Vectors

Displacement, Velocity & Acceleration

Displacement

Velocity

Acceleration

Representing Motion

Kinematic Equations

Motion Graphs

Reference Frames & Relative Motion

Vectors & Motion

Vectors & Motion in Two Dimensions

Projectile Motion

Unit 2: Force & Translational Dynamics

Systems & Center of Mass

Describing Systems

Center of Mass

Forces & Free-Body Diagrams

Free Body Diagrams

Forces as Interactions

Net Force

Translational Equilibrium

Newton's Laws

Newton's First Law

Newton's Second Law

Newton's Third Law

Tension

Tension

Tension in Ideal & Non-Ideal Strings

Gravitational Force

Newton's Law of Gravitation

Gravitational Force

Gravitational Field

Acceleration Due to Gravity

Gravitational Field Strength Equation

Weight

Apparent Weight

Inertial vs Gravitational Mass

Kinetic & Static Friction

Kinetic Friction

Kinetic Friction Force Equation

Static Friction

Static Friction Force Formula

Slipping & Sliding

Spring Forces

Hooke's Law

Circular Motion

Uniform Circular Motion

Acceleration in Circular Motion

Circular Motion in a Vertical Loop

Circular Motion Examples

Kepler's Third Law

Unit 3: Work, Energy & Power

Work

Defining Work & Work Done

Calculating Work Done

Translational Kinetic Energy & Potential Energy

Translational Kinetic Energy

Potential Energy

Elastic Potential Energy

Gravitational Potential Energy Near a Surface

Gravitational Potential Energy Between Objects