Study GuidesExam QuestionsPast Papers
AP®PhysicsCollege BoardPhysics 1: Algebra-BasedStudy GuidesUnit 1: KinematicsRepresenting MotionMotion Graphs

Motion Graphs (College Board AP® Physics 1: Algebra-Based): Study Guide

Leander Oates

Written by: Leander Oates

Reviewed by: Caroline Carroll

Updated on

Motion graphs

  • Graphs of position, velocity and acceleration as functions of time can be used to find the relationships between those quantities

  • When interpreting motion graphs, it is important to understand what information the graph shows

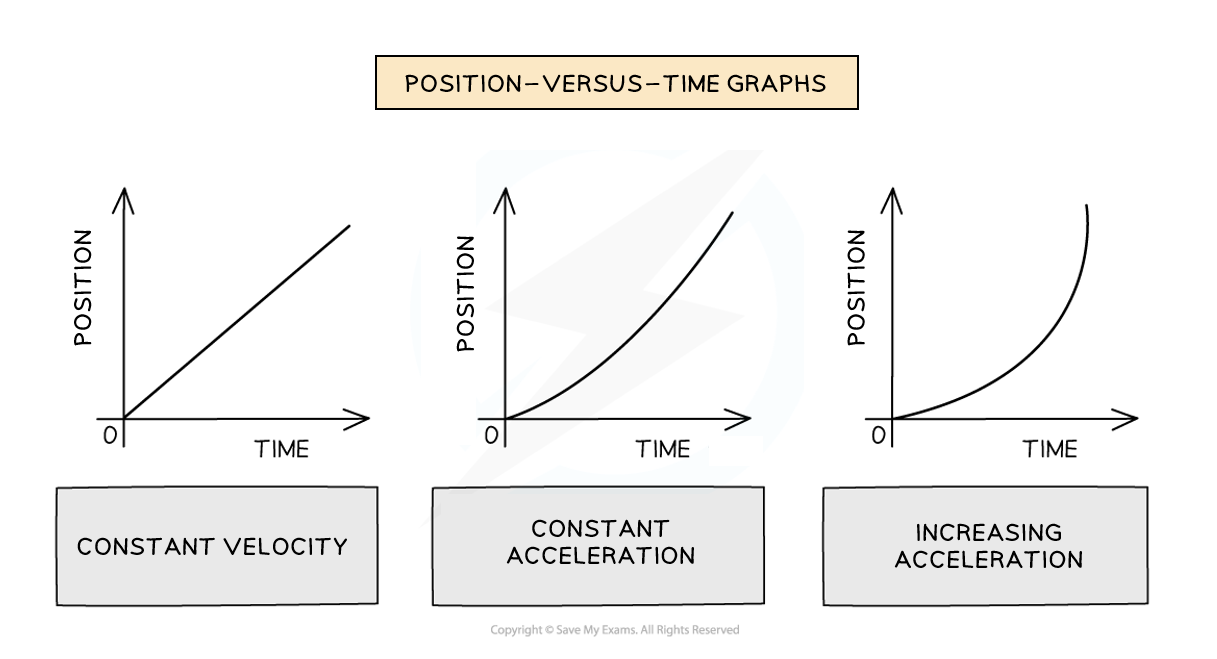
Position-versus-time graphs

  • Position-versus-time graphs are used to show the change in position or displacement of an object over time

  • On a position-versus-time graph:

    • Slope equals instantaneous velocity

    • The y-intercept equals the initial position

    • A constant gradient (slope) represents a constant velocity

    • A curved line represents an acceleration

    • A positive slope represents motion in the positive direction

    • A negative slope represents motion in the negative direction

    • A zero slope (horizontal line) represents a state of rest

    • The area under the curve means nothing

Three graphs comparing position versus time, labeled: constant velocity (linear), constant acceleration (quadratic), and increasing acceleration (exponential).
Constant velocity, constant acceleration, and increasing acceleration on a position-versus-time graph

Velocity-versus-time graphs

  • Velocity-versus-time graphs are used to show the change in velocity of an object over time

  • On a velocity-versus-time graph:

    • Slope equals acceleration

    • The y-intercept equals the initial velocity

    • A straight slope represents uniform acceleration

    • A curve represents non-uniform acceleration

    • A positive slope represents acceleration in the positive direction

    • A negative slope represents acceleration in the negative direction

    • A zero slope (horizontal line) represents motion with constant velocity

    • The area under the curve is equal to the displacement

Three velocity-time graphs showing constant velocity as a horizontal line, constant acceleration as a constant slope, and increasing acceleration as an upward curve with labeled axes for velocity and time.
Constant velocity, constant acceleration, and increasing acceleration on a velocity-versus-time graph

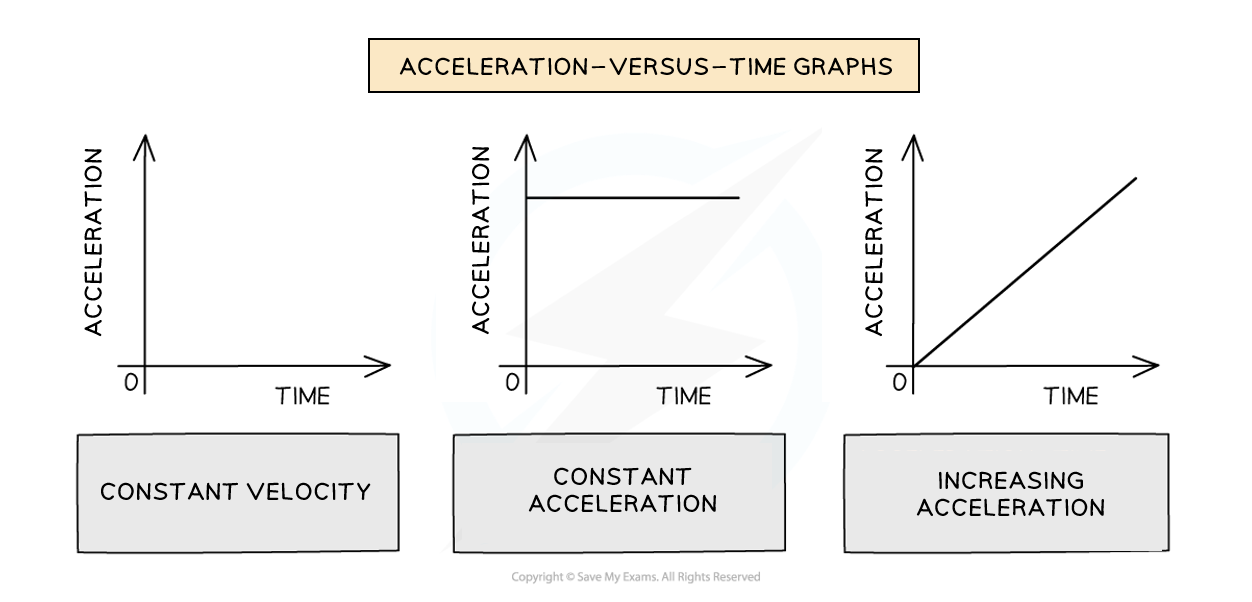
Acceleration-versus-time graphs

  • Acceleration-versus-time graphs are used to show the change in the acceleration of an object over time

  • On an acceleration-versus-time graph:

    • Slope means nothing

    • The y-intercept equals the initial acceleration

    • A zero slope (horizontal line) represents constant acceleration

    • The area under the curve equals the change in velocity

Three acceleration vs time graphs: flat line at zero for constant velocity, flat line above zero for constant acceleration, and a positive slope line for increasing acceleration.
Constant velocity, constant acceleration, and increasing acceleration on an acceleration-versus-time graph

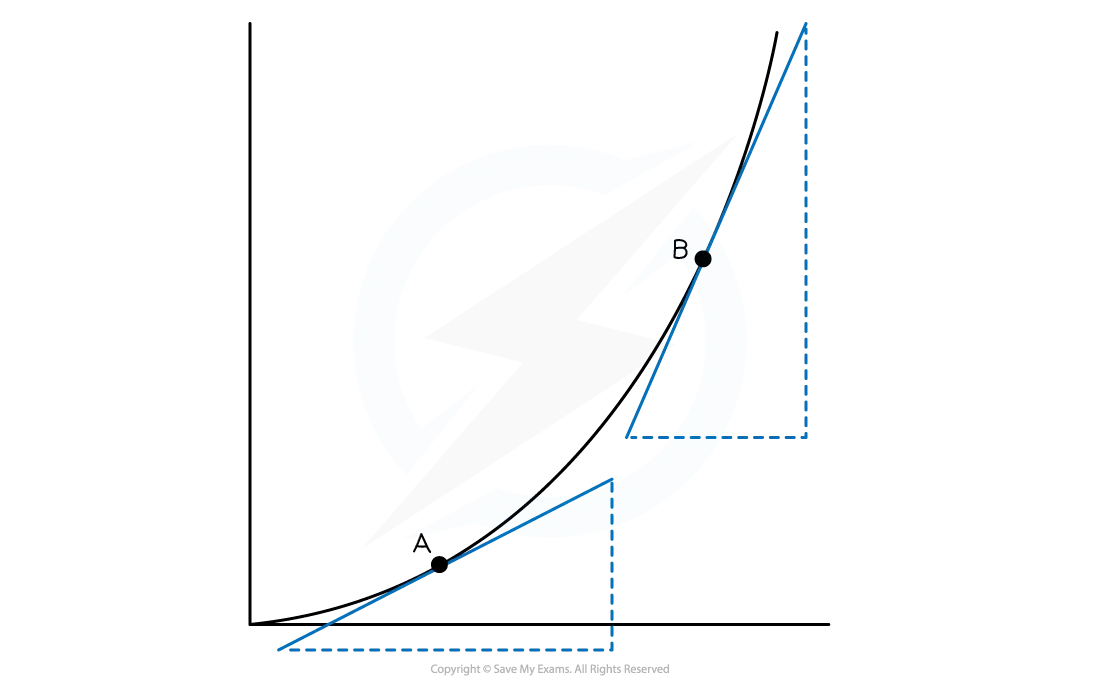
Calculating the slope of a motion graph

  • The slope of a straight line graph can be calculated using:

slope space equals space fraction numerator increment x over denominator increment y end fraction

Graph showing a right triangle formed by the x and y axes, with arrows indicating changes Δx and Δy. A box shows the slope formula: Slope = Δy/Δx.
The slope of a straight line can be calculated using the change in y divided by the change in x

  • The slope of a curve can be determined by drawing a tangent to a specific point on the curve and calculating the gradient of the tangent

    • A tangent should be drawn using a sharpened pencil and ruler for maximum accuracy

    • The slope of the tangent should be equal to the slope of the curve at that specific point

Graph showing a curve with two points labeled A and B. Both points have tangent lines forming right triangles with the x-axis. Points A and B's positions vary on the curve.
The slope of the tangent at point B is steeper than the slope of the tangent at point B. The slope can be calculated from the tangent to the curve

Worked Example

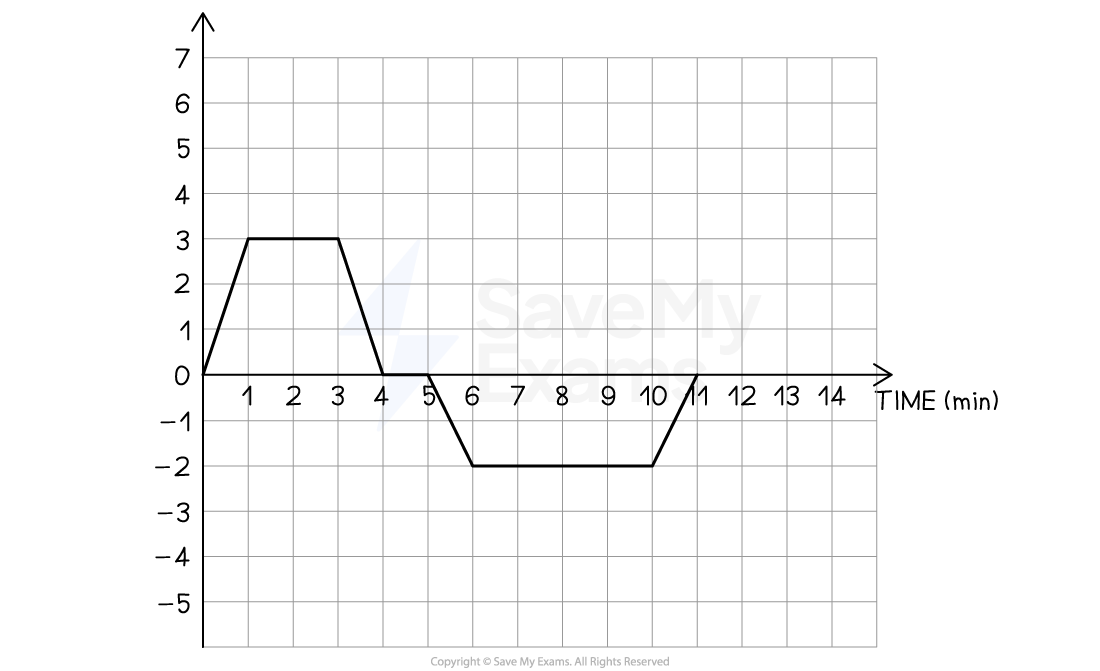
Line graph with time (min) on the X-axis and an unknown quantity on the Y-axis. The line goes from 0 - 3 in the first minute, remains at 3 for the next 2 minutes, then drops to zero over the next minute. The line remains at zero between minutes 4 and 5. The line then drops to -2 over the 5th minute, remains at -2 for 4 minutes and returns to zero over the 10th minute

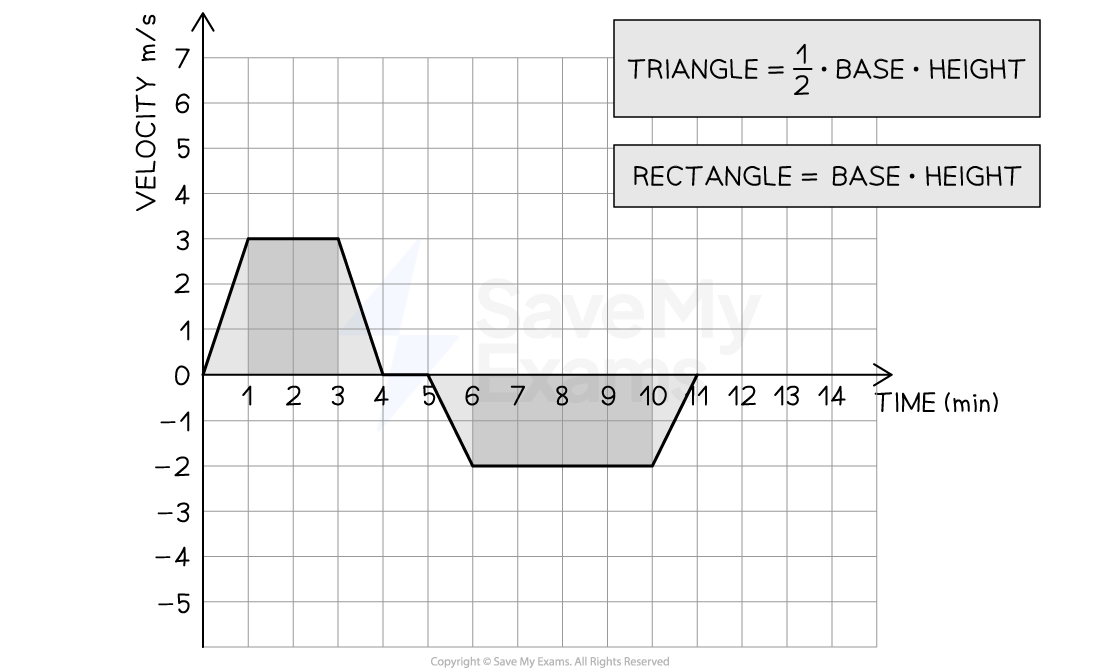
The above graph is a motion graph, which shows the motion of a taxicab. The driver initially turns on to a street at t space equals space 0 space and drives down the straight road, accelerating to a constant velocity. The driver then slows down, briefly stops, and then reverses some distance at a constant velocity back down the street.

(a) State the type of motion graph shown and justify your answer.

(b) Determine the displacement of the taxicab for the period shown in the graph and suggest a suitable unit.

(c) Sketch the other two types of motion graph for the taxicab's movements.

(d) At what time does the taxicab have the same position as when t space equals space 0?

Answer:

Part (a) State the type of motion graph shown and justify your answer

Step 1: Analyze the motion shown in the graph along with the narrative description

  • Over the first 5 minutes, the graph shows the y quantity increasing, then remaining constant, then decreasing to zero

    • This is consistent with a period of acceleration, followed by constant velocity, deceleration and a period of rest on a velocity-versus-time graph

    • This also matches the narrative description

  • Over the next 6 minutes, the graph shows the y quantity increasing in the negative direction, then remaining constant, then decreasing to zero

    • This is consistent with a period of acceleration in the negative direction, followed by constant velocity in the negative direction, and deceleration to zero on a velocity-versus-time graph

    • This also matches the narrative description

Step 2: State the type of motion graph

  • The graph is a velocity-versus-time graph

Step 3: Present evidence to justify your answer

  • The taxicab accelerates to a constant velocity

    • 0 - 1 min shows acceleration

    • 1 - 3 mins shows constant velocity

  • The taxicab slows to a stop

    • 3 - 4 mins shows a deceleration

    • 4 - 5 mins shows zero velocity

  • The taxicab reverses

    • 5 - 6 mins shows acceleration in the negative direction

    • 6 - 10 mins shows constant velocity in the negative direction

Part (b) Determine the displacement of the taxicab for the period shown in the graph and suggest a suitable unit

Calculate the area under the velocity-versus-time graph and give a suitable unit

Graph showing velocity (m/s) vs time (min) with shaded areas under sections. Includes formulas for area of triangle and rectangle.

increment x space equals space open parentheses 1 half space times space 1 space times space 3 close parentheses space plus space open parentheses 2 space times space 3 close parentheses space plus space open parentheses 1 half space times space 1 space times space 3 close parentheses space plus space open parentheses 1 half space times space 1 space times space minus 2 close parentheses space plus space open parentheses 4 space times space minus 2 close parentheses space plus space open parentheses 1 half space times space 1 space times space minus 2 close parentheses

increment x space equals space minus 1 space straight m

Part (c) Sketch the other two types of motion graph for the taxicab's movements

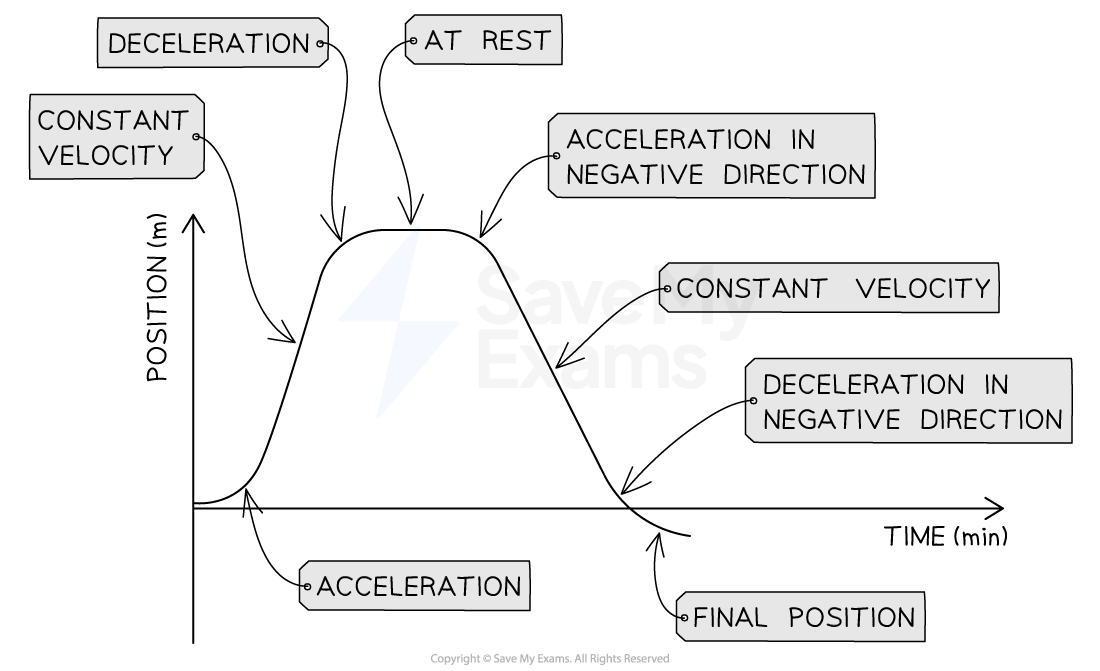
Step 1: Sketch the displacement-versus-time graph for the taxicab

  • Include all the changes in motion detailed on the velocity-versus-time graph

  • Keep the magnitudes proportional and the time roughly to scale

A position-time graph showing acceleration, the lines begins at the origin and increases in slope to form a curve, then an upward slope curving to a flat horizontal line, curving to a negative slope which curves at the bottom as it passes through to negative position quadrant

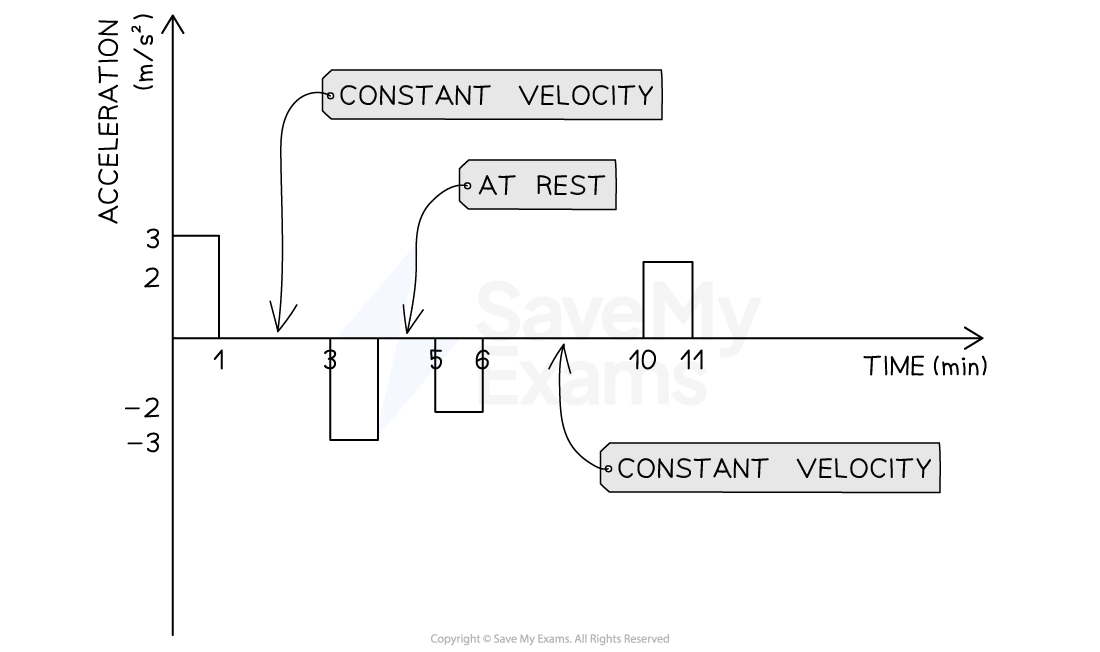
Step 2: Sketch the acceleration-versus-time graph for the taxicab

  • Include all the changes in motion detailed on the velocity-versus-time graph

  • Keep the magnitudes proportional and the time roughly to scale

A graph plotting acceleration (m/s²) against time (min). A period of positive acceleration for 1 s at 3 m/s², then zero acceleration for 3 s, then negative acceleration for 1 s at -3 m/s², then zero acceleration for 1 s. Then negative acceleration at 2 m/s² for 1 s, then zero acceleration for 4 s. Then positive acceleration for 1 s at 2 m/s²

Part (d) At what time does the taxicab have the same position as when t space equals space 0?

Step 1: Determine the displacement of the taxicab in the positive direction

increment x space equals space open parentheses 1 half space times space 1 space times space 3 close parentheses space plus space open parentheses 2 space times space 3 close parentheses space plus space open parentheses 1 half space times space 1 space times space 3 close parentheses space equals space 9 space straight m

Step 2: Determine the time at which the taxicab reaches an equal displacement in the negative direction

increment x space equals space open parentheses 1 half space times space 1 space times space minus 2 close parentheses space plus space open parentheses 4 space times space minus 2 close parentheses space equals space minus 9 space straight m

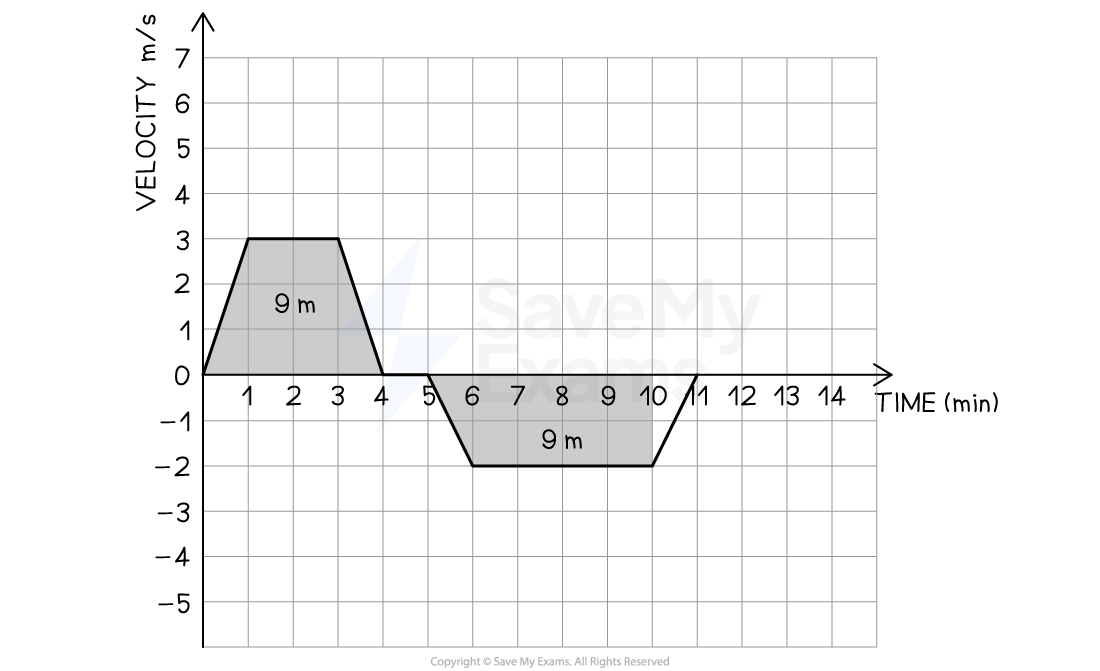
Graph showing two shaded trapezoids both labeled "9 m,"

  • The time at which the taxicab has equal displacements in the positive and negative directions occurs at 10 space straight s

    • This is when the taxicab passes its starting position

Examiner Tips and Tricks

When you are asked to justify your answer, you do not need to write in full sentences and paragraphs. Using bullet points is fine and will save you some time in the exam. The examiner will award marks for your reasoning in whatever form this is presented, as long as your logic is clearly expressed.

When asked to sketch a graph, you only need to draw the shape and label the axes. You do not need to annotate them or add specific values.

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Kinematic EquationsNext:Reference Frames & Relative Motion
    Author
    Reviewer
    Leander Oates

    Author: Leander Oates

    Expertise: Physics

    Leander graduated with First-class honours in Science and Education from Sheffield Hallam University. She won the prestigious Lord Robert Winston Solomon Lipson Prize in recognition of her dedication to science and teaching excellence. After teaching and tutoring both science and maths students, Leander now brings this passion for helping young people reach their potential to her work at SME.

    Caroline Carroll

    Author: Caroline Carroll

    Expertise: Physics Subject Lead

    Caroline graduated from the University of Nottingham with a degree in Chemistry and Molecular Physics. She spent several years working as an Industrial Chemist in the automotive industry before retraining to teach. Caroline has over 12 years of experience teaching GCSE and A-level chemistry and physics. She is passionate about creating high-quality resources to help students achieve their full potential.