Study GuidesExam QuestionsPast Papers
AP®PhysicsCollege BoardPhysics 1: Algebra-BasedStudy GuidesUnit 1: KinematicsDisplacement, Velocity & AccelerationVelocity

Velocity (College Board AP® Physics 1: Algebra-Based)

Study Guide

Leander Oates

Written by: Leander Oates

Reviewed by: Caroline Carroll

Average velocity

Speed

  • The speed of an object is defined as:

The distance traveled by an object per unit time

  • Speed is a scalar quantity with magnitude only

    • The direction of the object's motion is not described by speed

Average and instantaneous speed

The speedometer of a car gives a measure of instantaneous speed

  • For example, if the speedometer reads 50 miles per hour, which is 22 meters per second, it means that the car is traveling 22 meters in each second that this speed is maintained

Close-up of a car's speedometer, showing speeds from 0 to 260 km/h, with glowing red indicators and diesel fuel gauge at half.
The speedometer on a vehicle displays instantaneous speed

Image: Creative commons licence from pxhere.com

  • As the speed of the car changes, the speedometer will give a new value for the new instantaneous speed

    • The instantaneous speed is the speed at which an object travels in each instant of time

  • Average speed, on the other hand, describes the whole journey

  • Average speed considers the total distance traveled and the total time taken

    • For example, the car will not travel at 22 meters per second for its entire journey; it will speed up and slow down accordingly

average space speed space equals space fraction numerator total space distance space traveled over denominator total space time space taken end fraction

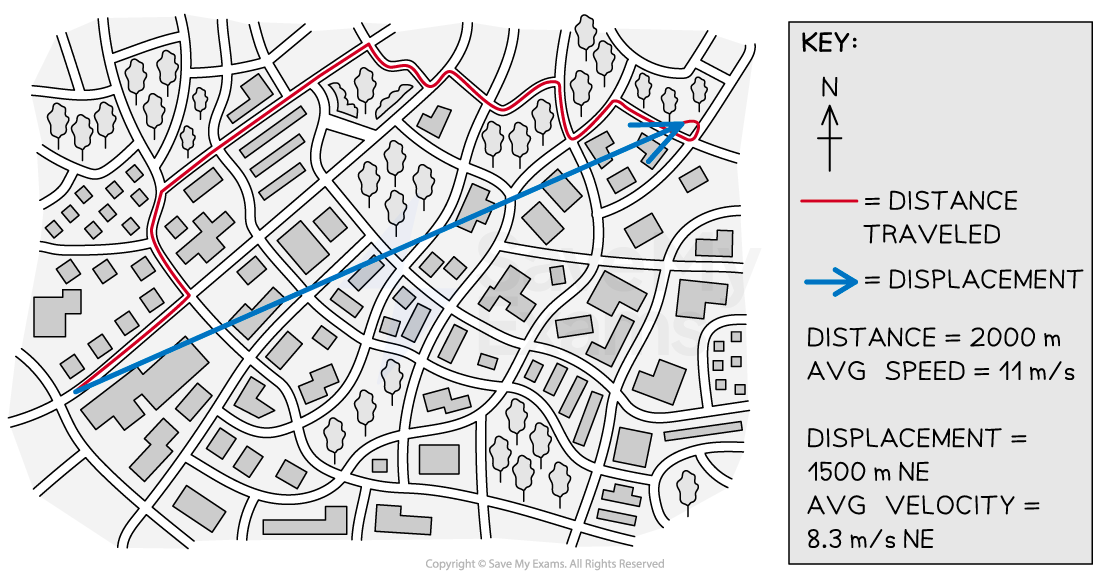
  • If the car traveled a total distance of 2000 meters and the whole journey took 3 minutes, which is 180 seconds, then the average speed of the car was 11 meters per second

average space speed space equals fraction numerator space 2000 over denominator 180 end fraction space equals space 11 space straight m divided by straight s

Map showing distance traveled by car

A hand-drawn map of a town with irregular grid roads and buildings. A red line shows a winding route labeled "Distance traveled." A north arrow is in the top right.
The red line shows the distance traveled by the car over its 3 minute journey

Velocity

  • The velocity of an object is defined as:

The displacement of an object per unit time

  • In other words, the rate of change of an object's position

  • Velocity is a vector quantity with both magnitude and direction

    • If an object travels with a constant speed but changes direction, then its velocity is changing

    • Therefore, it is possible for an object to travel at a constant speed without a constant velocity, but it is not possible for an object to travel at a constant velocity without a constant speed

  • The magnitude of an object's velocity is its speed

    • However, the magnitude of an object's average velocity is not its average speed

Average and instantaneous velocity

  • Average velocity also describes the whole journey of an object

  • Average velocity considers the initial and final states of an object over an interval of time

    • In other words, the displacement of an object over the total time taken

v with rightwards arrow on top subscript a v g end subscript space equals space fraction numerator increment x with rightwards arrow on top over denominator increment t end fraction

  • Where:

    • v with rightwards arrow on top subscript a v g end subscript = average velocity, measured in straight m divided by straight s

    • increment x with rightwards arrow on top = displacement, measured in straight m

    • increment t = time interval, measured in straight s

  • If the car had a displacement of 1500 meters over its 3 minute journey, then its average velocity would be 8.3 meters per second travelling north-east for that same car trip

v with rightwards arrow on top subscript a v g end subscript space equals space 1500 over 180 space equals space 8.3 space straight m divided by straight s space NE

Map showing displacement of car

Map showing a red winding path for distance travelled and a straight blue line for displacement. Includes a key and data: distance 2000m, displacement 1500m NE.
Map showing distance traveled in red and displacement in blue. Since these values are different, the average speed and the average velocities are also different.

  • Calculating the average velocity over a very small time interval yields a value that is very close to the instantaneous velocity

Negative velocity

  • Since velocity is a vector quantity, it can have a positive or negative value

  • A positive velocity value indicates an object is traveling in the initial direction of motion

  • A negative value of velocity indicates that an object is traveling in the opposite direction

  • If there is no initial direction of motion, then positive velocity is generally either:

    • forwards

    • to the right

    • upwards

  • However, mathematically, any direction can be assigned as positive as long as the opposing direction is negative

Examiner Tips and Tricks

Whichever direction you assign as positive, make sure you are consistent throughout your calculation.

Worked Example

The map below shows a high school teacher's 4 minute route through the city on their way to work. The teacher travels 1.8 km along a straight road, then turns left and travels a further 450 m before parking their car.

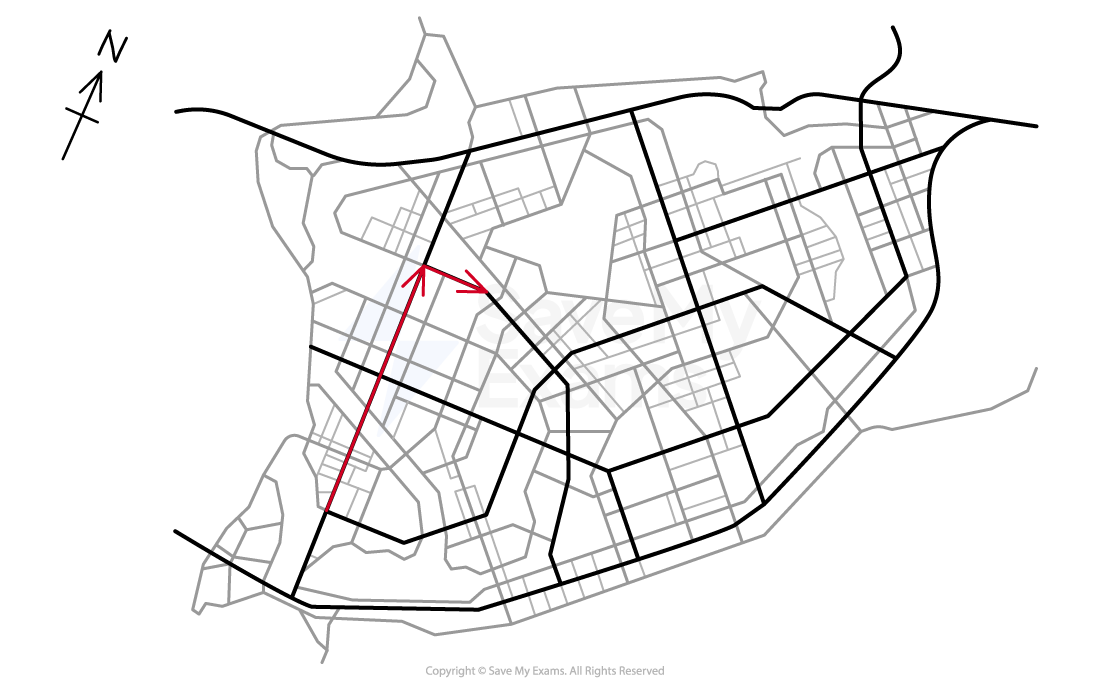
City street map with a red arrow pointing upwards along a major vertical road heading north, then turning a corner onto another street heading east. A compass indicating north is in the upper-left corner.

What is the ratio of the teacher's average speed to average velocity?

A: 1.1

B: 1.2

C: 1.3

D: 1.4

The correct answer is B

Answer:

Step 1: Analyze the scenario

  • The roads that the teacher traveled on are perpendicular

    • The length of the displacement vectors on the northbound and eastbound roads are known

    • These vectors can be added using trigonometry to give the resultant displacement vector

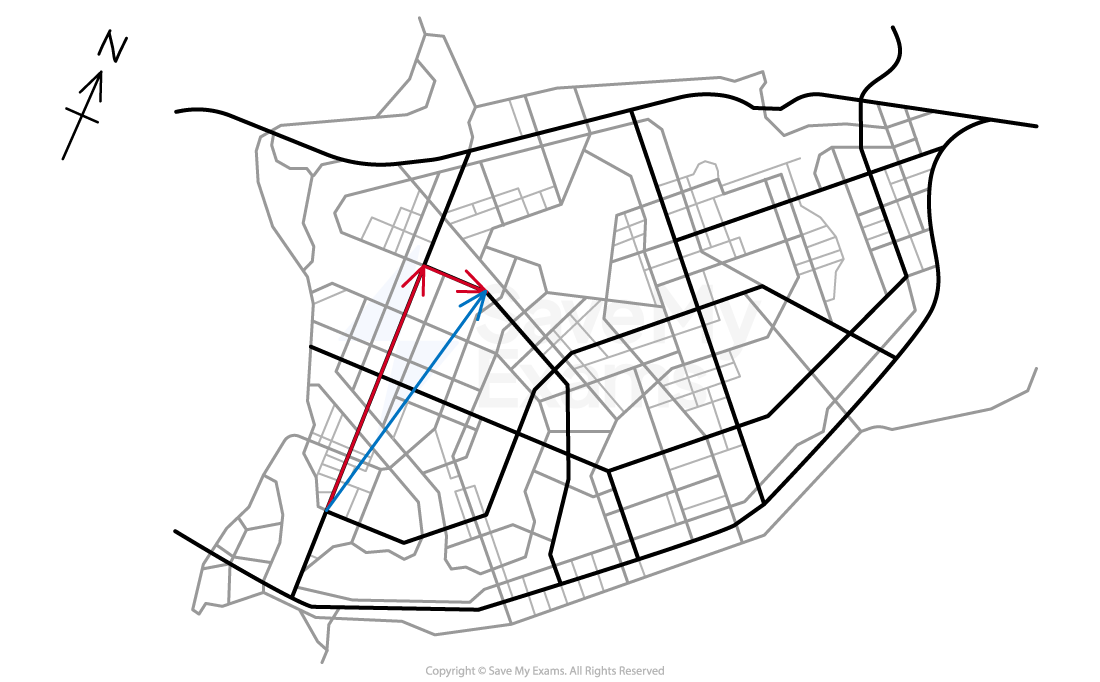
The same city map shows the resultant displacement vector forming the hypotenuse of a triangle with the north and east-bound vectors.

  • The average velocity of the teacher can then be calculated using the displacement and the time interval of the journey

  • The total distance traveled is the non-vector sum of the lengths of the displacement vectors on the northbound and eastbound roads

Step 2: List the known quantities

  • Displacement on northbound road, x subscript N space equals space 1.8 space km space equals space 1800 space straight m

  • Displacement on eastbound road, x subscript E space equals space 450 space straight m

  • Time interval, increment t space equals space 4 space min space equals space 4 space times space 60 space straight s space equals space 240 space straight s

Step 3: Determine the displacement

  • Using trigonometry, where c is the hypotenuse and therefore increment x

c squared space equals space a squared space plus space b squared

increment x squared space equals space x subscript N squared space plus space x subscript E squared

increment x space equals space square root of 1800 squared space plus space 450 squared end root

increment x space equals space 1855 space straight m space NE

Step 4: Calculate the average velocity

v with rightwards arrow on top subscript a v g end subscript space equals space 1855 over 240 space equals space 7.73 space straight m divided by straight s space NE

Step 5: Calculate the average speed

  • Determine the total distance traveled

total space distance space equals space 1800 space plus space 450 space equals space 2250 space straight m

  • Determine the average speed

average space speed space equals space fraction numerator total space distance space traveled over denominator total space time space taken end fraction

average space speed space equals fraction numerator space 2250 over denominator 240 end fraction space equals space 9.38 space straight m divided by straight s

Step 6: Calculate the ratio of average speed to average velocity

fraction numerator average space speed over denominator average space velocity end fraction space equals space fraction numerator 9.38 over denominator 7.73 end fraction space equals space 1.21

1.21 space equals space 1.2 space open parentheses 2 space straight s. straight f. close parentheses

  • This is answer B

Examiner Tips and Tricks

The gap between the question and the answer can seem huge at first glance. It is important that you do not panic when you first read a question. All the information you require to answer the question will always be provided for you; you just need to think logically about how you can use that information to get the quantities you actually want.

Last updated:

You've read 0 of your 5 free study guides this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:DisplacementNext:Acceleration
    Author
    Reviewer
    Leander Oates

    Author: Leander Oates

    Expertise: Physics

    Leander graduated with First-class honours in Science and Education from Sheffield Hallam University. She won the prestigious Lord Robert Winston Solomon Lipson Prize in recognition of her dedication to science and teaching excellence. After teaching and tutoring both science and maths students, Leander now brings this passion for helping young people reach their potential to her work at SME.

    Caroline Carroll

    Author: Caroline Carroll

    Expertise: Physics Subject Lead

    Caroline graduated from the University of Nottingham with a degree in Chemistry and Molecular Physics. She spent several years working as an Industrial Chemist in the automotive industry before retraining to teach. Caroline has over 12 years of experience teaching GCSE and A-level chemistry and physics. She is passionate about creating high-quality resources to help students achieve their full potential.