Displacement (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself

Author

Leander Oates

Expertise

Physics

How to calculate displacement

Defining an object

The term object can be used to describe a wide range of items in physics, from subatomic particles to entire galaxies
When the term object is used to describe something, the assumption is that the following properties are ignored:
- size
- shape
- internal configuration
The object may be treated as:
- a point mass
- a point charge

Position

Position is defined as:

An object's location in space, relative to a reference point

In math, the position of an object is measured relative to the origin of a coordinate system

Graph with x and y axes originating from (0,0). A red cross marks a position connected to the origin by a dotted line labeled "position vector." — **In math, the position of a point is measured relative to the origin of a coordinate system**

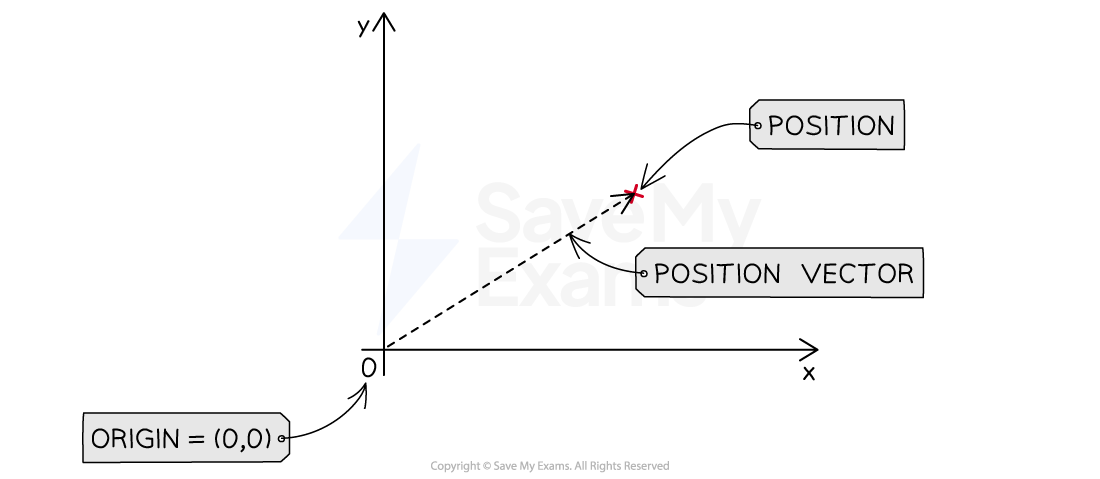
In physics, the position of an object, $x$ , is measured relative to a reference point
The reference point could be a coordinate system or another object
- For example, point A is located at the coordinate (5, 3)
- Or, the car is located at 4 m to the left of the lamp post
The relative nature of an object's position gives it a directional component
This is why position is a vector quantity with both magnitude and direction

Displacement

Displacement is defined as:

The change in an object's position

Displacement describes the difference in position between an object's starting position and its finishing position, regardless of the route taken
- Distance is the route traveled; this is covered in detail in the study guide on Scalar and vector quantities
Since displacement describes the movement of an object from its initial position to its final position, displacement is also a vector quantity with both magnitude and direction
Displacement is described algebraically using the following equation:

$∆ x = x - x_{0}$

Where:
- $∆ x$ = displacement, measured in $m$
- $x$ = final position, measured in $m$
- $x_{0}$ = initial position, measured in $m$
Notice that the $∆ x$ notation literally means a change in position

Worked Example

On an $x$ , $y$ coordinate system, Object 1 moves from (1, 1) to (7, 1) to (3, 1). Object 2 moves from (4, 3) to (1, 3) to (7, 3) and Object 3 moves from (5, 5) to (9, 5) to (1, 5).

Which of the following statements is true?

A: $|∆ x_{1}| > |∆ x_{2}| > |∆ x_{3}|$

B: $|∆ x_{1}| = |∆ x_{2}| = |∆ x_{3}|$

C: $|∆ x_{2}| > |∆ x_{1}| > |∆ x_{3}|$

D: $|∆ x_{3}| > |∆ x_{2}| > |∆ x_{1}|$

The correct answer is D

Answer:

Step 1: Analyze the scenario

The $y$ coordinates for each object are constant, so the objects are moving in one dimension only
Object 1 moves in the positive direction from (1, 1) to (7, 1), then it moves in the negative direction from (7, 1) to (3, 1)
Object 2 moves in the negative direction from (4, 3) to (1, 3), then it moves in the positive direction from (1, 3) to (7, 3)
Object 3 moves in the positive direction from (5, 5) to (9, 5), then it moves in the negative direction from (9, 5) to (1, 5)
Recall that displacement is the change in an object's position from its initial position to its final position

Step 2: Sketch a diagram of the situation or calculate the displacement algebraically

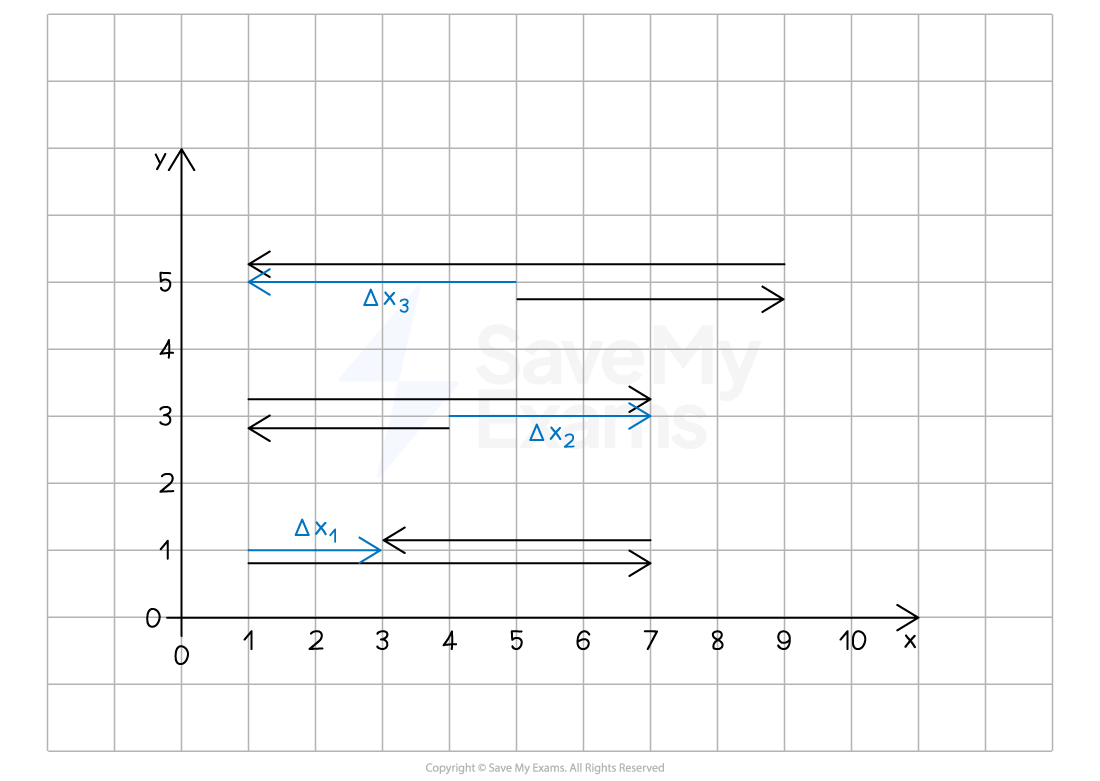
A graph with x and y axes shows different horizontal vectors. Black arrows show the movement of the objects, blue arrows show the net movement from the starting positions to the final positions.

On the diagram:
- The lower black arrows show the movement of each object from its initial position to its intermediate position
- The upper black arrows show the movement of each object from its intermediate position to its final position
- The blue arrows show the net movement of each object from its initial position to its final position; this is the object's displacement
Calculating algebraically using the equation

$∆ x = x - x_{0}$

Object 1
- Initial position on $x$ -axis, $x_{0} = 1$
- Final position on $x$ -axis, $x = 3$

$∆ x_{1} = 3 - 1 = 2$

Object 2
- Initial position on $x$ -axis, $x_{0} = 4$
- Final position on $x$ -axis, $x = 7$

$∆ x_{2} = 7 - 4 = 3$

Object 3
- Initial position on $x$ -axis, $x_{0} = 5$
- Final position on $x$ -axis, $x = 1$

$∆ x_{3} = 1 - 5 = - 4$

Step 3: Review the answer options

The answer options describe the relative values for the magnitude of the displacement, $|∆ x|$ so the direction of the displacement can be ignored
The object with the greatest magnitude of displacement is Object 3
The object with the smallest magnitude of displacement is Object 1

$4 > 3 > 2$

Therefore:

$|∆ x_{3}| > |∆ x_{2}| > |∆ x_{1}|$

This is answer option D

Examiner Tip

Displacement is a straight line from the object's starting position, $x_{0}$ , to its final position, $x$ , therefore, the vector arrow of displacement will always lie along a single plane. So, when displacement is expressed in terms of the object's starting position, the direction is already stated in the $x_{0}$ term. Hence, vector notation is not required if the $x_{0}$ term is present.

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Next topic

Did this page help you?