Tension in Ideal & Non-Ideal Strings (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself

Author

Ann Howell

Expertise

Physics Content Creator

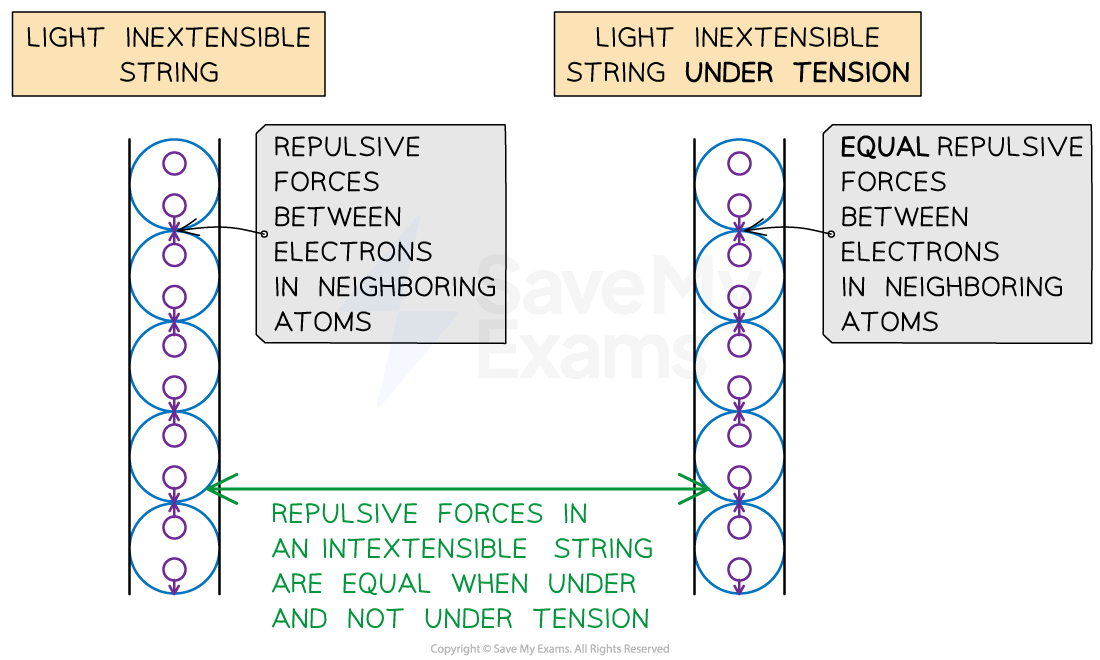
Tension in ideal strings

An ideal string has negligible mass and does not stretch when under tension
- An ideal string is described as inextensible
An ideal string can also refer to an ideal
- cable
- chain
- wire
- rope
The tension in an ideal string is the same at all points within the string
An ideal string does not exist in reality, but they are used in model systems to simplify calculations

An ideal string under tension

Repulsive forces between electrons in neighbouring atoms of an inextensible string, equal whether string is under tension or not. — **A light inextensible string under and not under tension both have equal repulsive forces between electrons.**

Worked Example

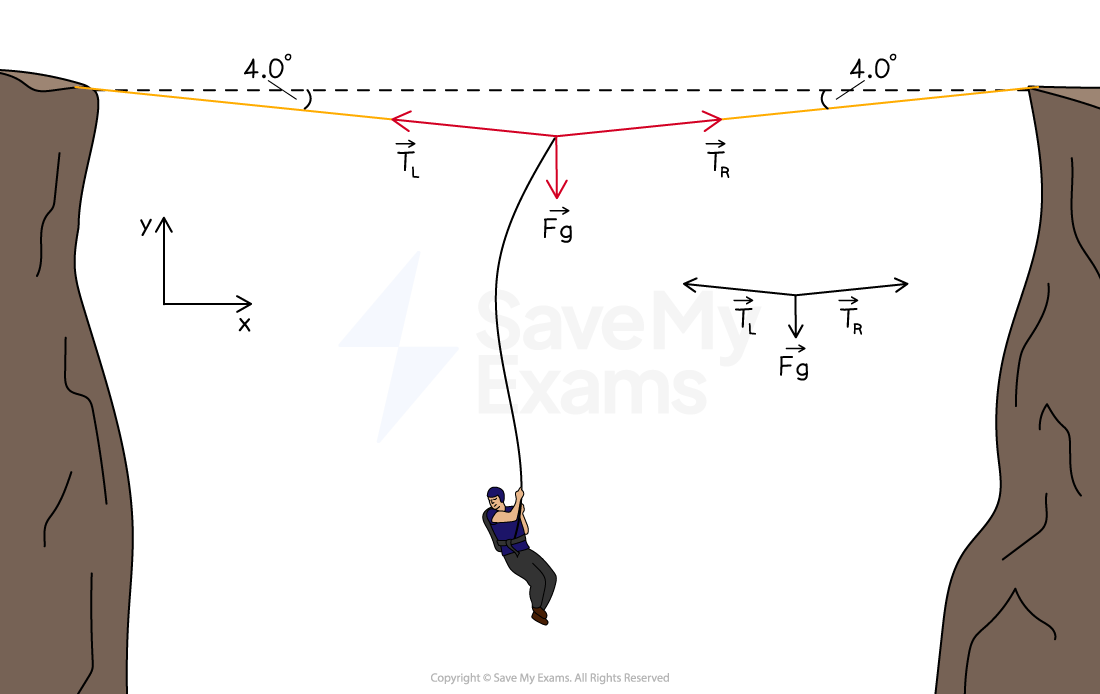
A person of mass $55 kg$ has fallen off a slack line stretched under tension between the peaks of two mountains. The person is suspended by a light inextensible string at the mid point of the slack line, equidistant from each peak. The weight of the person has caused the slack line to sink at an angle of $4.0 °$ to the horizontal. The person and the slack line are stationary.

A person is hanging from the middle of a slack line. Tension forces TL and TR are shown at 4-degree angles. Cartesian plane axes are labeled.

Which of the following gives the magnitude of the tension in the slack line?

A $550 N$

B $393 N$

C $3928 N$

D $7857 N$

The correct answer is C

Answer:

Step 1: Analyze the scenario

The slack line is assumed to be an ideal string
- So tension is uniform along it
- and its mass is negligible
The slack line is not completely horizontal because of the person's weight
- This means the slack line has both vertical and horizontal components of tension
The system is stationary, so the tension in the left side ${\vec{T}}_{L}$ must equal the tension in the right side ${\vec{T}}_{R}$
- So, ${\vec{T}}_{L} = {\vec{T}}_{R} = \vec{T}$

Step 2: Determine the vertical component of the tension in the slack line

Draw a diagram and label the sides of the tension triangle in relation to the angle to the horizontal $4.0 °$

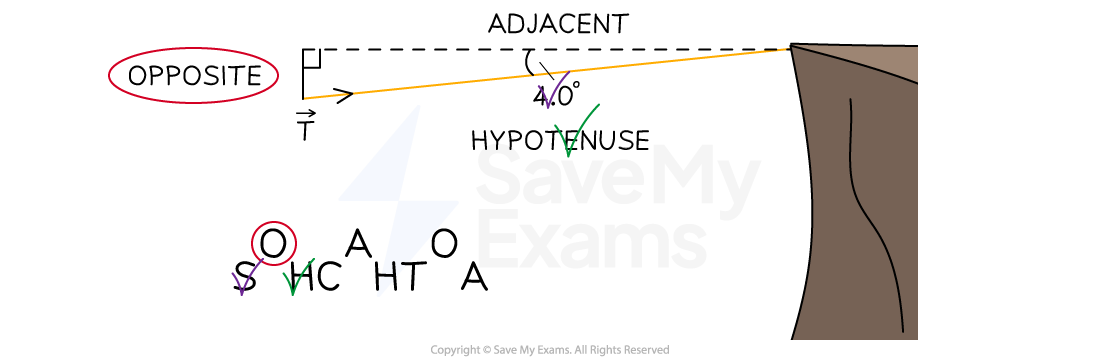
SOHCAHTOA mnemonic with a right angled triangle illustration showing components: opposite, adjacent, hypotenuse. The mnemonic letters are handwritten and color-coded.

Determine the correct trigonometric function to calculate the vertical component of tension ${\vec{T}}_{y}$

$opposite = \sin (θ) \cdot hypotenuse$

$opposite = \sin (4.0) \cdot \vec{T}$

${\vec{T}}_{y} = 0.07 \vec{T}$

Step 3: Resolve the system of forces acting on the slack liner vertically

${\vec{F}}_{g} = 0.07 {\vec{T}}_{L} + 0.07 {\vec{T}}_{R}$ $g g g$

$\vec{F_{g}} = 0.14 \vec{T}$

Step 4: Calculate the magnitude of the tension in the slack line

${\vec{F}}_{g} = m \vec{g} = 0.14 \vec{T}$

$(55 \times 10) = 0.14 \vec{T}$

$\vec{T} = \frac{550}{0.14}$

$\vec{T} = 3928 N$

Therefore, option C is correct

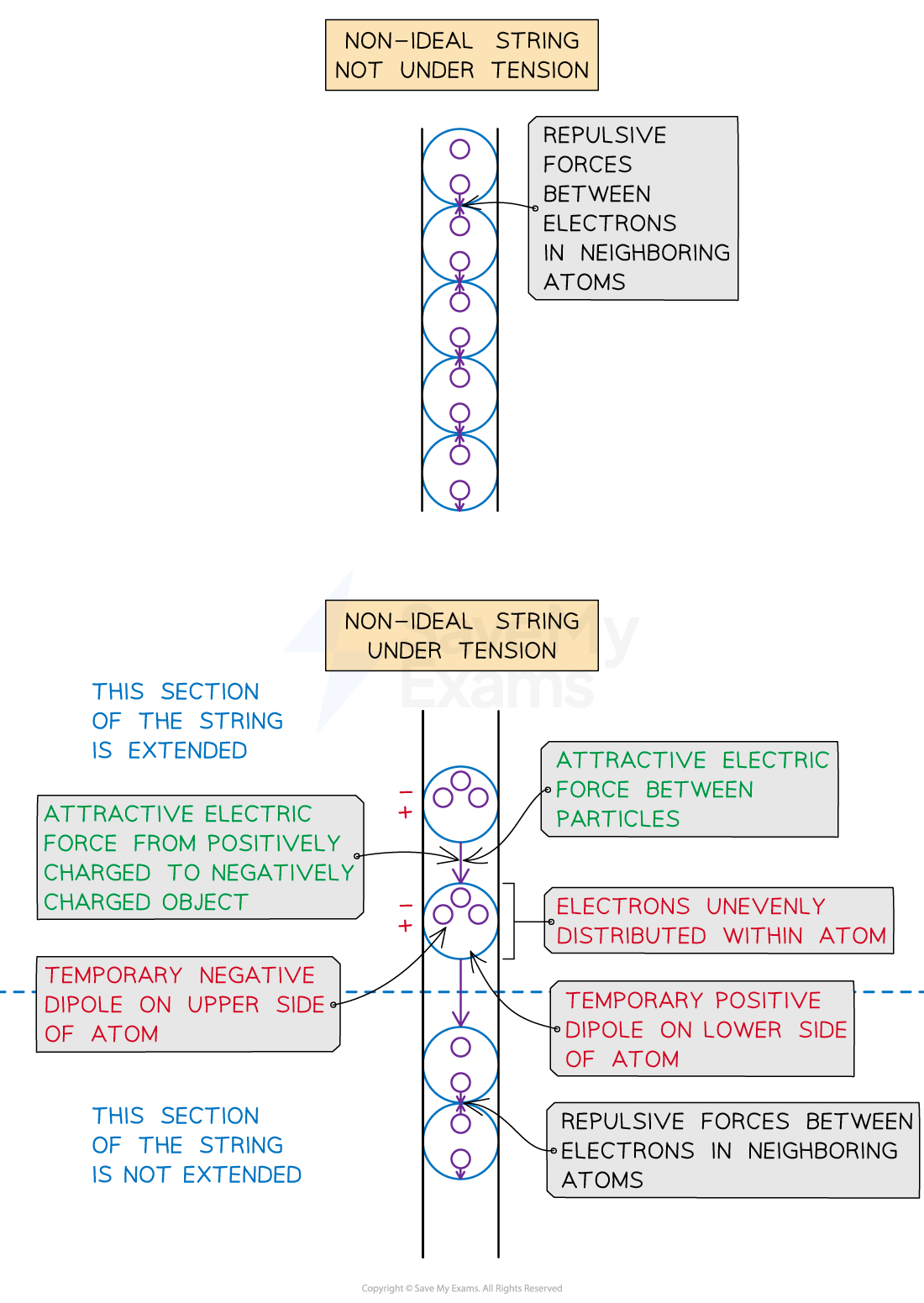
Tension in non-ideal strings

In a string with nonnegligible mass, tension may not be the same at all points within the string
- So a non-ideal string has an extension that may not be the same at all points
A non-ideal string can also refer to a non-ideal
- cable
- chain
- wire
- rope
In reality all strings are non-ideal
- There is more extension in some points than in others

A non-ideal string under tension

Comparing non-ideal string under tension and non-tension, showing repulsive and attractive electric forces, notes on dipoles, and electron distribution in atoms. — **A non-ideal string extends by different amounts at different points**

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Next topic

Did this page help you?