Center of Mass (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself

Written by: Katie M

Reviewed by: Caroline Carroll

Center of mass

The center of mass of a system is defined as:

The point where all of an object’s mass can be thought to be concentrated

When a system consists of a single object:
- it can be modeled as a point particle that is located at the system's center of mass
- all interactions can be considered to act at the system's center of mass

Diagram of a broom balanced on a pivot showing the center of mass, with the handle extending left and the bristles on the right. — **The center of mass of a single object is the point where all of its mass is thought to act, as a result, it is the point the weight of the object acts.**

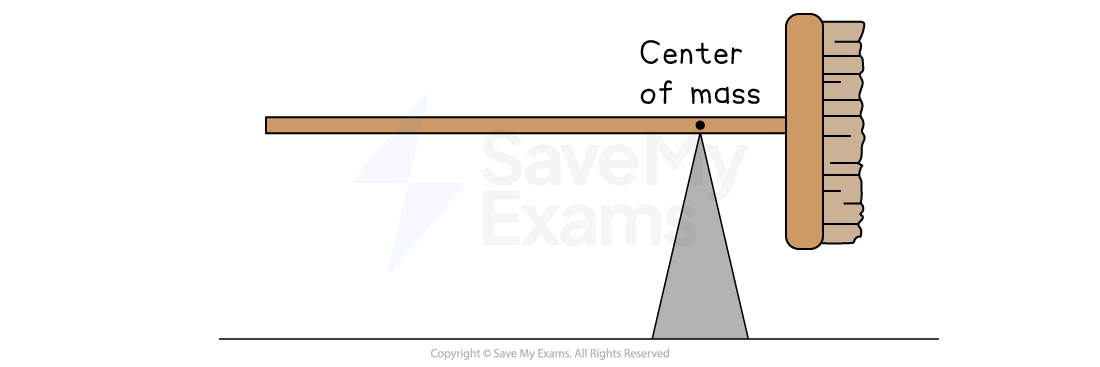
When a system consists of multiple objects:
- each object can be modeled as a point particle, with an associated mass and position which contributes to the system's center of mass
- interactions between objects within a system (i.e. internal forces) do not influence the motion of a system’s center of mass

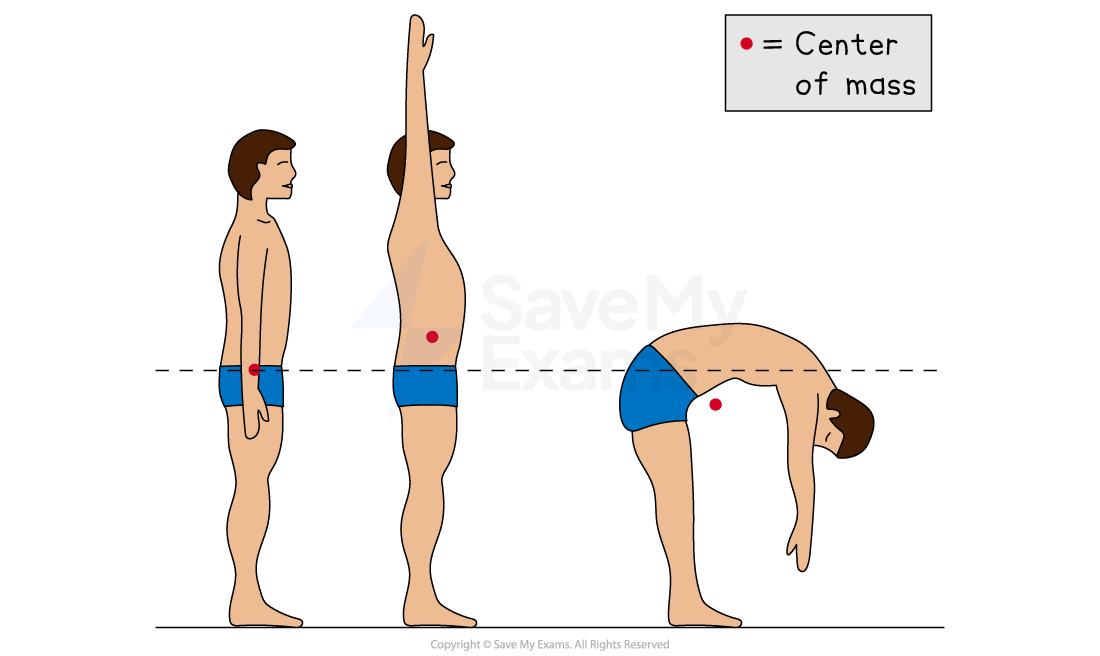
Examiner Tips and Tricks

Remember, the center of mass is a hypothetical point, so it can lie inside or outside of a body. The center of mass of a non-rigid body can change depending on its shape. For example, a person’s center of mass is lower when learning forward than when standing upright

Diagram showing a person in three poses: standing, reaching up, and bending forward, with a label indicating the center of mass shifts.

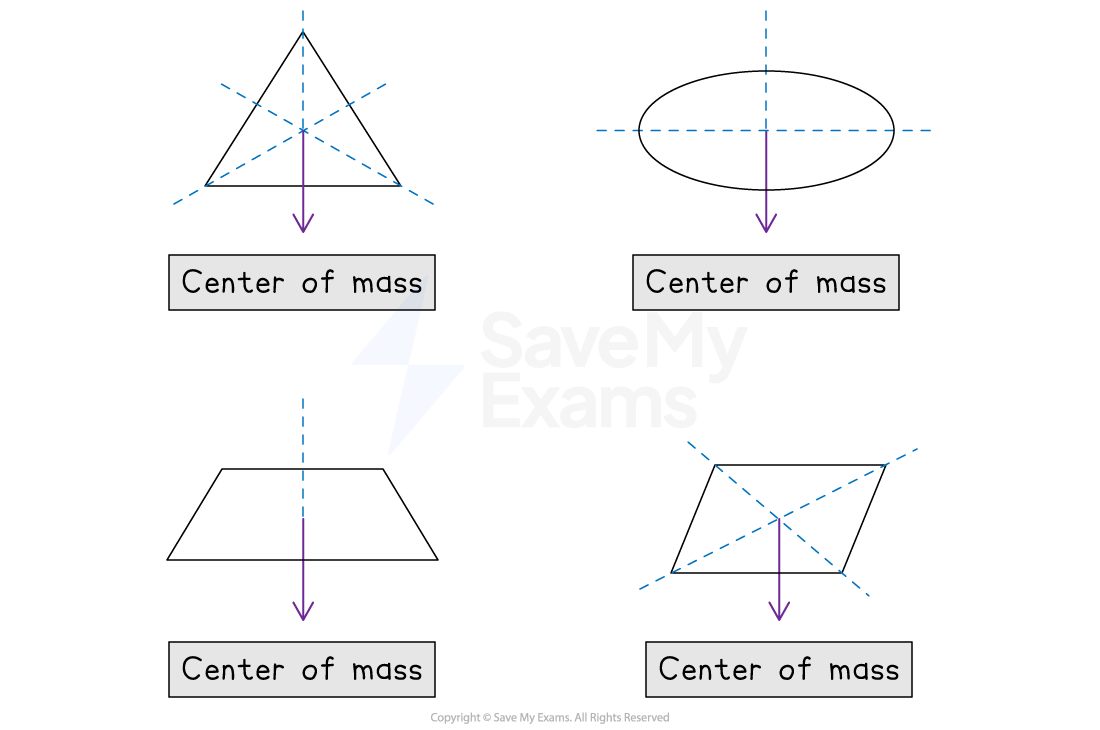
Locating center of mass

For systems with symmetrical mass distributions, the center of mass is located on lines of symmetry

Center of mass of a symmetrical object

Four shapes with lines indicating the center of mass: triangle, oval, trapezoid, and parallelogram, each labeled "CENTRE OF MASS."

The location of a system’s center of mass along a given axis can be calculated using the equation:

${\vec{x}}_{c m} = \frac{\sum_{i} m_{i} {\vec{x}}_{i}}{\sum_{i} m_{i}}$

Where:
- ${\vec{x}}_{c m}$ = position of the system's center of mass, in $m$
- $m_{i}$ = mass of each object, in $kg$
- ${\vec{x}}_{i}$ = position of each object, in $m$

Calculating the center of mass of a 1D system

Consider a system of three objects located along the same line
The position of the system's center of mass can be determined using:

${\vec{x}}_{c m} = \frac{m_{1} x_{1} + m_{2} x_{2} + m_{3} x_{3}}{m_{1} + m_{2} + m_{3}}$

Position of the center of mass on a line

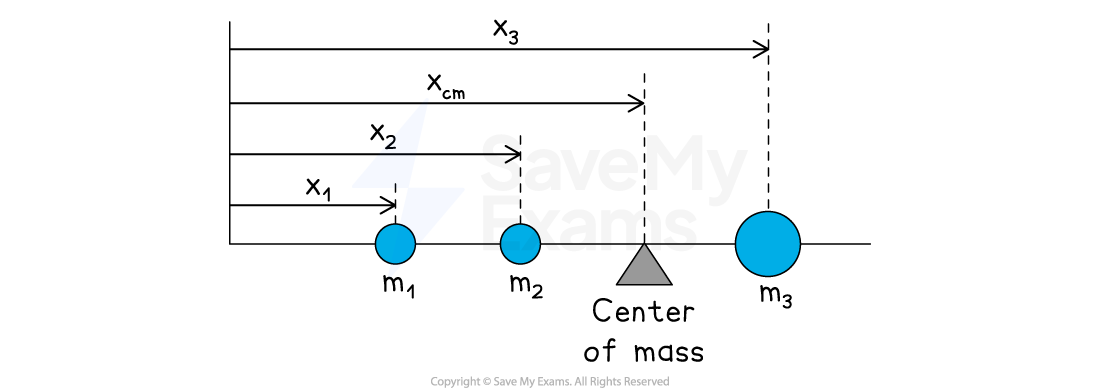
Diagram showing three masses m1, m2, and m3 on a line with distances x1, x2, x3 from the origin. A triangle marks the center of mass. — **The center of mass of a system of particles along the same line will be located somewhere along that line**

Calculating the center of mass of a 2D system

Consider a system of three objects located along the same x-y plane
The position of the system's center of mass can be determined using:

${\vec{r}}_{c m} = \frac{\sum_{i} (m_{i} {\vec{r}}_{i})}{\sum m_{i}} = \frac{m_{1} {\vec{r}}_{1} + m_{2} {\vec{r}}_{2} + m_{3} {\vec{r}}_{3}}{m_{1} + m_{2} + m_{3}}$

Where:
- ${\vec{r}}_{c m}$ = position vector of the system's center of mass, in $m$
- ${\vec{r}}_{i}$ = position vector of each particle, in $m$

Position of the center of mass on an x-y plane

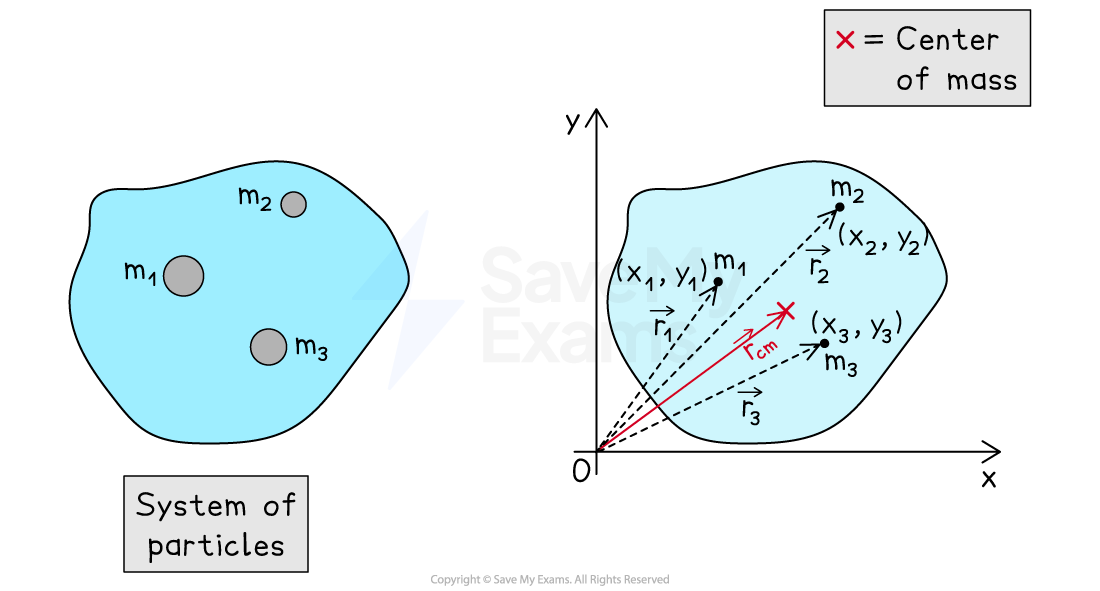
Diagram of a system of particles, showing masses m1, m2, and m3 in pink shapes. The center of mass is marked with vectors and coordinates. — **A system of particles along the same x-y plane can be described in terms of the position of the system's center of mass**

The positions of the separate x and y coordinates of the system's center of mass can be determined using:

${\vec{x}}_{c m} = \frac{m_{1} x_{1} + m_{2} x_{2} + m_{3} x_{3}}{m_{1} + m_{2} + m_{3}}$

${\vec{y}}_{c m} = \frac{m_{1} y_{1} + m_{2} y_{2} + m_{3} y_{3}}{m_{1} + m_{2} + m_{3}}$

Using Pythagoras' theorem, the magnitude of the position vector is:

${\vec{r}}_{c m} = \sqrt{{({\vec{x}}_{c m})}^{2} + {({\vec{y}}_{c m})}^{2}}$

Using trigonometry, the direction of the position vector can be found from:

$\tan θ = \frac{{\vec{y}}_{c m}}{{\vec{x}}_{c m}}$

Examiner Tips and Tricks

In AP Physics 1, you will only be expected to calculate the center of mass for systems of five or fewer particles arranged in a two-dimensional configuration or for highly symmetrical systems

Last updated: 18 October 2024

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself

Did this page help you?

Previous:Describing SystemsNext:Free Body Diagrams

Center of Mass (College Board AP® Physics 1: Algebra-Based)

Study Guide

Center of mass

Examiner Tips and Tricks

Locating center of mass

Center of mass of a symmetrical object

Calculating the center of mass of a 1D system

Position of the center of mass on a line

Calculating the center of mass of a 2D system

Position of the center of mass on an x-y plane

Examiner Tips and Tricks

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Katie M

Author: Caroline Carroll