Hooke's Law (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself

Author

Caroline Carroll

Expertise

Physics Subject Lead

Ideal spring

When a spring is neither stretched nor compressed, it is said to be in equilibrium
- The net force on the spring is zero
- Its length at its equilibrium position is known as the relaxed length
When a spring is stretched or compressed, its change in length (extension or compression), $Δ \vec{x}$ , is the displacement from its equilibrium position
- The spring will exert a force, ${\vec{F}}_{s}$ , towards its equilibrium position

Force exerted by a spring

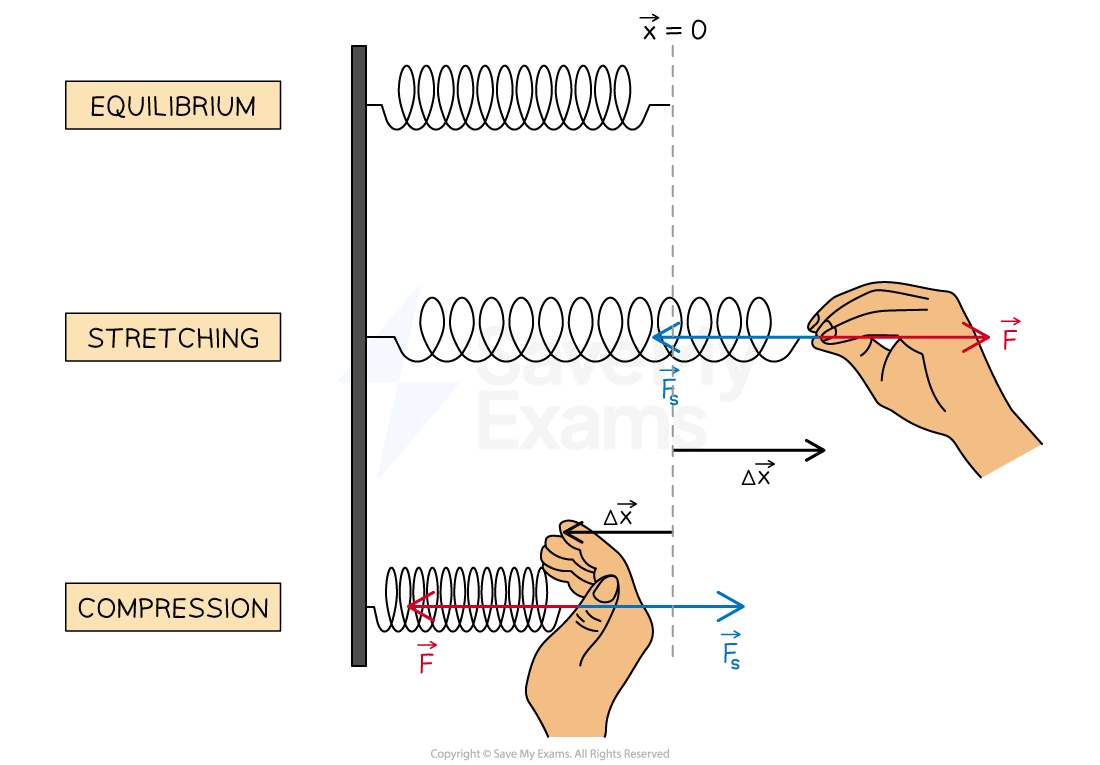
Diagram showing forces on a spring in three states: equilibrium, stretching, and compression. Arrows indicate applied force (F), spring force (Fs) and change in length (Δx) — **A spring is in equilibrium when it is not stretched or compressed. When it is stretched or compressed, the force it exerts is towards the equilibrium position.**

An ideal spring can be defined as:

A spring that has negligible mass and exerts a force that is proportional to the change in its length as measured from its relaxed length

This can be expressed as:

${\vec{F}}_{s} \propto - Δ \vec{x}$

Where:
- ${\vec{F}}_{s}$ = force exerted by a spring, in $N$
- $Δ \vec{x}$ = change in length of the spring, in $m$
The minus sign shows that the force exerted by a spring is a restoring force as it acts toward the equilibrium position

Hooke's law

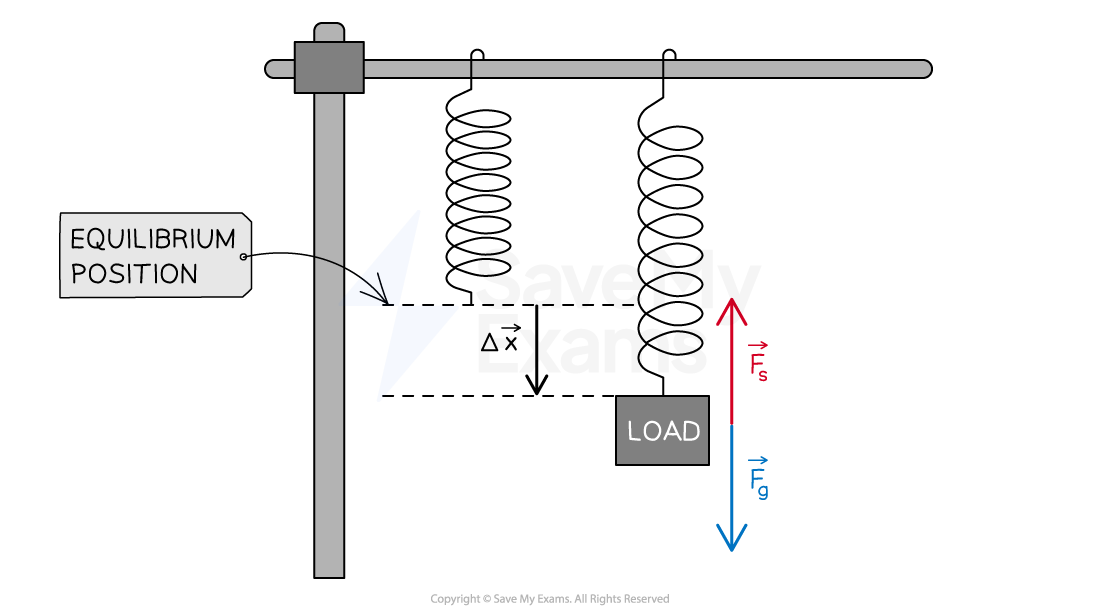
When an object is placed on an ideal spring, the spring will exert a force on the object
For an ideal spring:

${\vec{F}}_{s} \propto - Δ \vec{x}$

Where:
- ${\vec{F}}_{s}$ = force exerted by a spring, in $N$
- $Δ \vec{x}$ = change in length of the spring, in $m$
This can be re-written using a proportionality constant, called the spring constant, to show the magnitude of this force
This equation is known as Hooke's law:

${\vec{F}}_{s} = - k Δ \vec{x}$

Where:
- ${\vec{F}}_{s}$ = force exerted by a spring, in $N$
- $k$ = spring constant, in $N / m$
- $Δ \vec{x}$ = change in length, in $m$

The force that is exerted by an ideal spring on an object is a restoring force
Hooke's law applies to both extensions and compressions:
- The extension of an object is determined by how much it has increased in length
- The compression of an object is determined by how much it has decreased in length
The extension, $Δ x$ , is the difference between the relaxed and stretched length

$extension = stretched length - relaxed length$

Force exerted on an object by an ideal spring

Diagram showing a spring system with a load hanging from it, labeled with equilibrium position, displacement (Δx), spring force (Fs) upwards, and weight (Fg) downwards. — **The force exerted by an ideal spring acting on the object is towards the equilibrium position of the object-spring system**

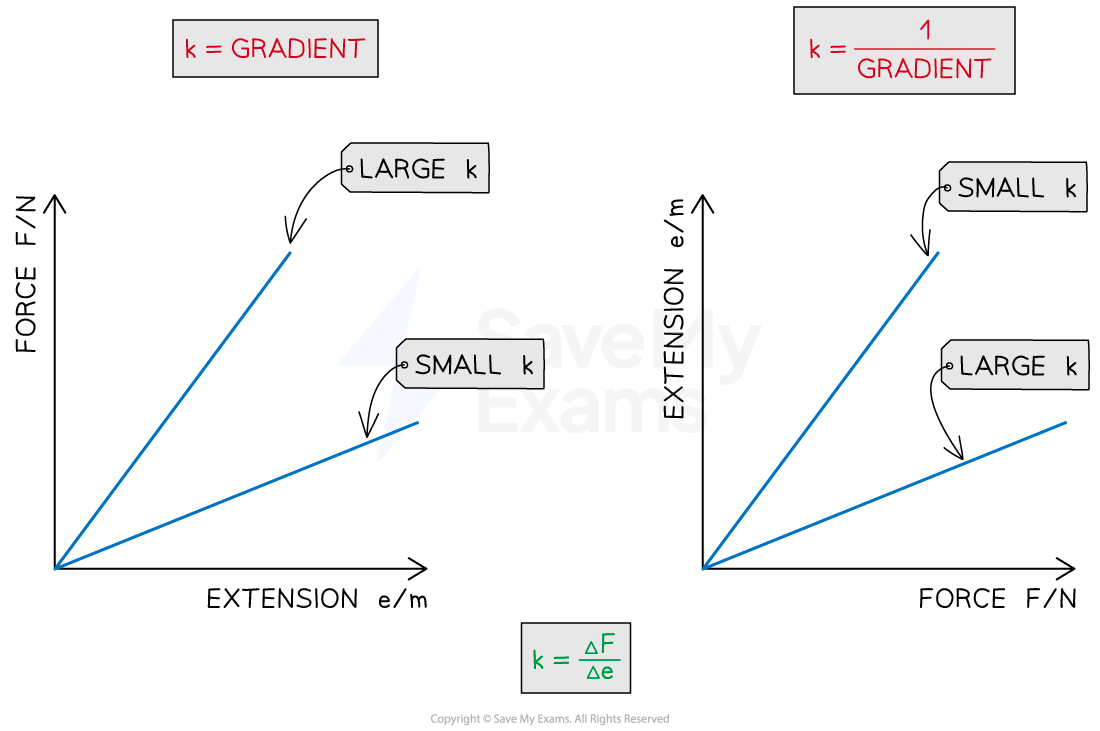
Force-versus-extension graphs

The relationship between force and the change in length from its relaxed length is shown on a force-versus-extension graph
- For an ideal spring, this is a linear relationship shown as a straight-line graph which passes through the origin

Calculating the spring constant from a force-versus-extension graph

Two graphs compare force vs. extension and extension vs. force. Left: Force vs. extension with large k having a steeper slope. Right: Extension vs. force with large k having a less steep slope. — **The spring constant is the slope, or 1 ÷ slope of a force-versus-extension graph depending on which variable is on which axis**

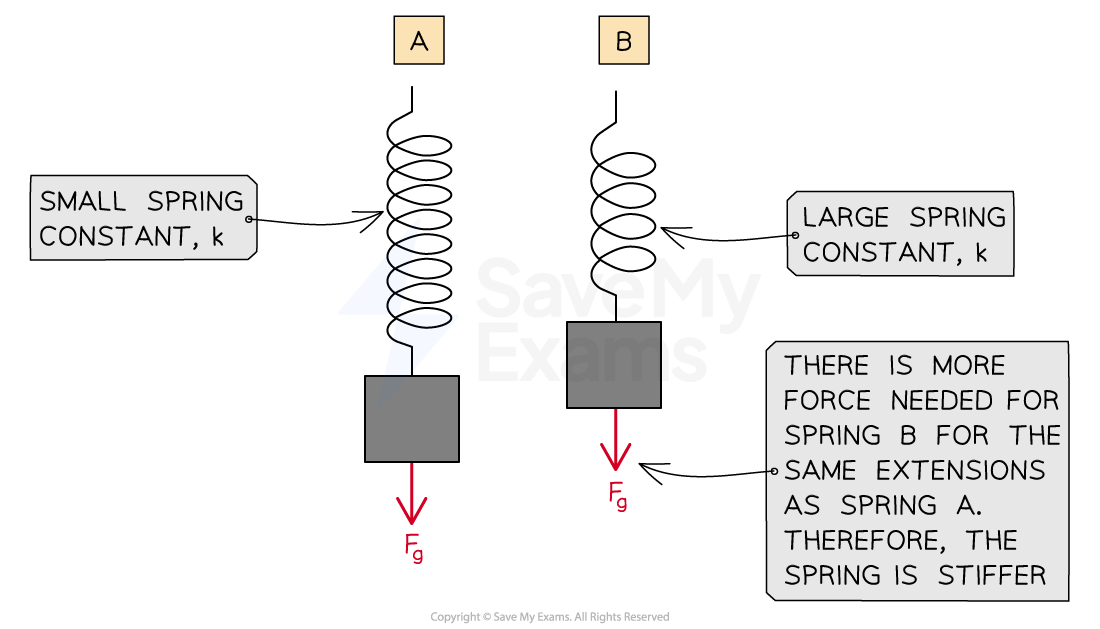
The stiffer the spring, the greater the spring constant and vice versa
- This means that more force is required per meter of extension compared to a less stiff spring
When force is plotted against extension, the steeper the slope of the line, the larger the spring constant and the stiffer the spring

Diagram comparing two springs with weights, showing spring A with a small spring constant and spring B with a large spring constant. Spring B is stiffer. — **Spring B has a larger spring constant than spring A, therefore spring B needs more force per unit extension (it is stiffer)**

Combination of springs

Springs can be combined in different ways:
- In series (end-to-end)
- In parallel (side-by-side)
The effective spring constant, $k_{e f f}$ , is a measure of how much force the combination of springs exerts per unit of extension or compression

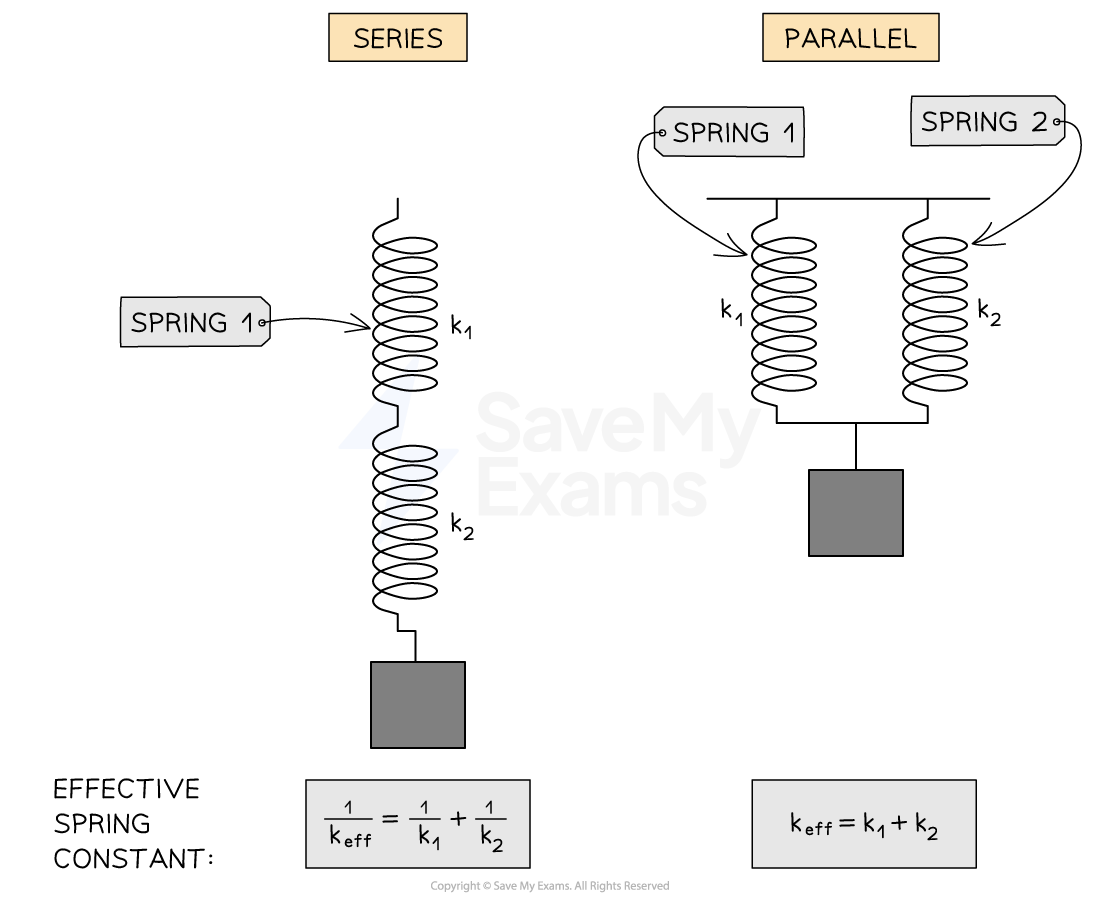
Diagram showing springs in series and parallel configurations. Series equation: 1/kff = 1/k1 + 1/k2. Parallel equation: keff = k1 + k2. — **Springs can be connected in series or parallel. The effective spring constant depends on how the springs are connected**

Springs in parallel

For springs in parallel, the extension from the equilibrium position, $Δ \vec{x}$ , is the same for both springs
The net force exerted by the two springs, ${\vec{F}}_{e f f}$ , is:

${\vec{F}}_{e f f} = {\vec{F}}_{1} + {\vec{F}}_{2}$

Using Hooke's law, the force exerted by spring 1 is:

${\vec{F}}_{1} = - k_{1} Δ \vec{x}$

The force exerted by spring 2 is:

${\vec{F}}_{2} = - k_{2} Δ \vec{x}$

Substituting:

${\vec{F}}_{e f f} = (- k_{1} Δ \vec{x}) + (- k_{2} Δ \vec{x}) = - (k_{1} + k_{2}) Δ \vec{x}$

Therefore, the effective spring constant for springs in parallel, $k_{e f f}$ , is:
$k_{e f f} = k_{1} + k_{2}$

Springs in series

For springs in series, the total extension, $Δ \vec{x}$ is:

$Δ \vec{x} = Δ {\vec{x}}_{1} + Δ {\vec{x}}_{2}$

Where:
- $Δ {\vec{x}}_{1}$ is the extension of spring 1, measured in $m$
- $Δ {\vec{x}}_{2}$ is the extension of spring 2, measured in $m$
The force is evenly distributed, so the force, $F$ , exerted by each spring is equal
The extensions can be written in terms of force and spring constants using Hooke's law:

$Δ \vec{x_{1}} = - \frac{\vec{F}}{k_{1}}$

$Δ \vec{x_{2}} = - \frac{\vec{F}}{k_{2}}$

Therefore

$Δ \vec{x} = (- \frac{\vec{F}}{k_{1}}) + (- \frac{\vec{F}}{k_{2}}) = - (\frac{1}{k_{1}} + \frac{1}{k_{2}}) \vec{F}$

Rearranging this in the format of Hooke's law for a single spring:

$\vec{F} = - k Δ \vec{x}$

$\vec{F} = - (\frac{1}{\frac{1}{k_{1}} + \frac{1}{k_{2}}}) Δ \vec{x} = - (\frac{k_{1} k_{2}}{k_{1} + k_{2}}) Δ \vec{x}$

Therefore, the effective spring constant, $k_{e f f}$ , is:

$k_{e f f} = \frac{k_{1} k_{2}}{k_{1} + k_{2}}$

Worked Example

Four springs are arranged vertically as shown in the figure.

Three springs, O, P, and Q hang downwards. They are connected to a fourth spring, R, which hangs beneath spring P. Spring R is connected to a weight labeled W, hanging downwards.

Springs P, Q and O are identical and each has a spring constant $k$ . Spring R has a spring constant of $4 k$ . What is the magnitude of the increase in the overall length of the arrangement when a force, $\vec{W}$ is applied as shown in the figure?

A $\frac{12 k}{7 W}$

B $\frac{6 W}{5 k}$

C $\frac{7 W}{12 k}$

D $\frac{2 W}{5}$

The correct answer is C

Answer:

Step 1: Analyze the scenario

Springs O, P and Q are in parallel and act like a single spring with an effective spring constant, $k_{O P Q}$
The three springs O, P and Q act like a single spring with a spring constant $k_{O P Q}$ which is in series with spring R
The effective spring constant of the arrangement, $k_{e f f}$

Step 2: Identify the equation to calculate the overall increase in length of the arrangement

Rearranging Hooke's law gives the equation for the overall increase of the arrangement:

$Δ \vec{x} = - \frac{\vec{F}}{k_{e f f}} = - \frac{\vec{W}}{k_{e f f}}$

Step 3: Calculate the effective spring constant

The effective spring constant from parallel springs O, P and Q

$k_{O P Q} = k_{O} + k_{P} + k_{Q} = k + k + k = 3 k$

The springs O, P and Q are in series with spring R, so the effective spring constant of the arrangement can be calculated by:

$\frac{1}{k_{e f f}} = \frac{1}{3 k} + \frac{1}{4 k} = \frac{7}{12 k}$

$k_{e f f} = 1 \div \frac{7}{12 k} = \frac{12 k}{7}$

Step 3: Substitute back into the equation for the equation for the overall increase in length of the arrangement

$Δ \vec{x} = - \frac{\vec{W}}{k_{e f f}} = - \frac{7 \vec{W}}{12 k}$

The negative sign indicates that the direction of the increase is in the opposite direction to the force exerted by the spring

Examiner Tip

The effective spring constant equations for combined springs work for any number of springs e.g. if there are 3 springs in parallel $k_{1}$ , $k_{2}$ and $k_{3}$ the effective spring constant would be $k_{e f f} = k_{1} + k_{2} + k_{3}$ .

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Next topic

Did this page help you?