Newton's Second Law (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself

Author

Ann Howell

Expertise

Physics Content Creator

Newton's second law

Newton’s second law of motion states:

The acceleration of a system’s center of mass has a magnitude proportional to the magnitude of the net force exerted on the system and is in the same direction as that net force

Newton's second law of motion is defined by the equation:

${\vec{a}}_{s y s} = \frac{\sum \vec{F}}{m_{s y s}} = \frac{{\vec{F}}_{n e t}}{m_{s y s}}$

Where:
- ${\vec{a}}_{s y s}$ = acceleration of the system's center of mass, measured in $m / s^{2}$
- ${\vec{F}}_{n e t}$ = net force exerted on the system, measured in $N$
- $m_{s y s}$ = mass of the system, measured in $kg$
Newton's second law states that:
- acceleration is directly proportional to the net external force
- acceleration is inversely proportional to the mass of the system
The velocity of a system’s center of mass will only change if a nonzero net external force is exerted on that system
- Remember that a system can be modeled as a singular object with a center of mass at the center of the system

Mass and net external force

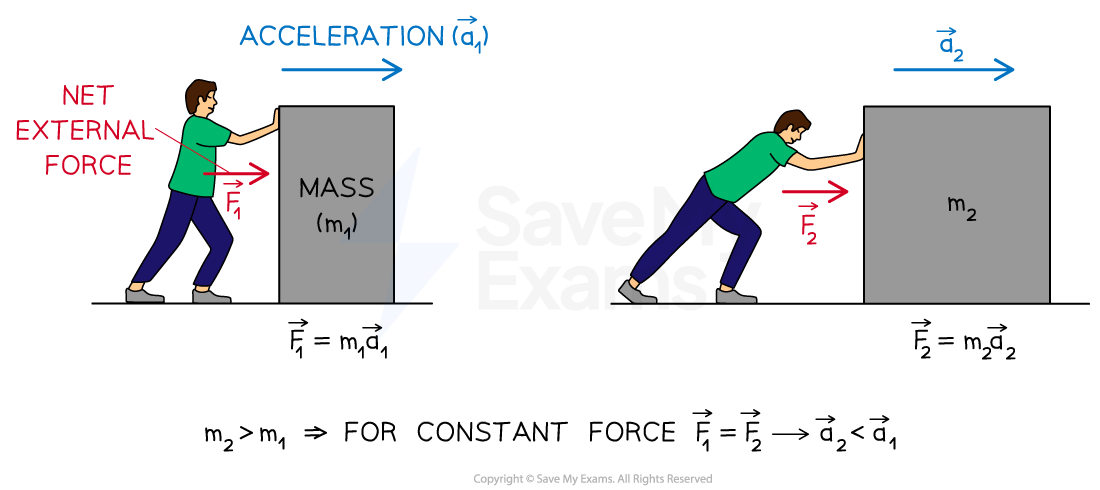
Two blue figures pushing different masses labeled 'm1' and 'm2' with red force arrows 'F1' and 'F2' and blue acceleration arrows labeled 'a'. Equations describe the relationship between mass, forces and acceleration — **According to Newton's second law mass is inversely proportional to acceleration**

Forces can combine to produce:
- balanced forces when the net external force is zero
- unbalanced forces when the net external force is nonzero

Newton's second law in two dimensions

Motion can be investigated in one or two-dimensional planes, such as along the ground or on a slope
- One-dimensional planes involve just up and down or left and right (on the ground)
- Two-dimensional planes involve both up and down and left and right (on an inclined plane)
Forces may be balanced in one dimension but unbalanced in another
- The system’s velocity will change only in the direction of the unbalanced force
On an inclined plane, one dimension is parallel to the plane of the slope and the other dimension is perpendicular to the plane of the slope
An object can have:
- unbalanced forces acting down the slope causing it to accelerate down the slope
- balanced forces acting perpendicular to the slope so there is no motion away from or into the inclined plane of the slope

Worked Example

A rocket of mass $0.8 \times 10^{5} kg$ produces an upward thrust of $15 MN$ and has a weight of $8 MN$ . When in flight, the force due to air resistance is $500 kN$ .

What is acceleration of the rocket?

A $- 187.5 m / s^{2}$

B $- 81 m / s^{2}$

C $81 m / s^{2}$

D $87.5 m / s^{2}$

The correct answer is C

Answer:

Step 1: Analyze the scenario

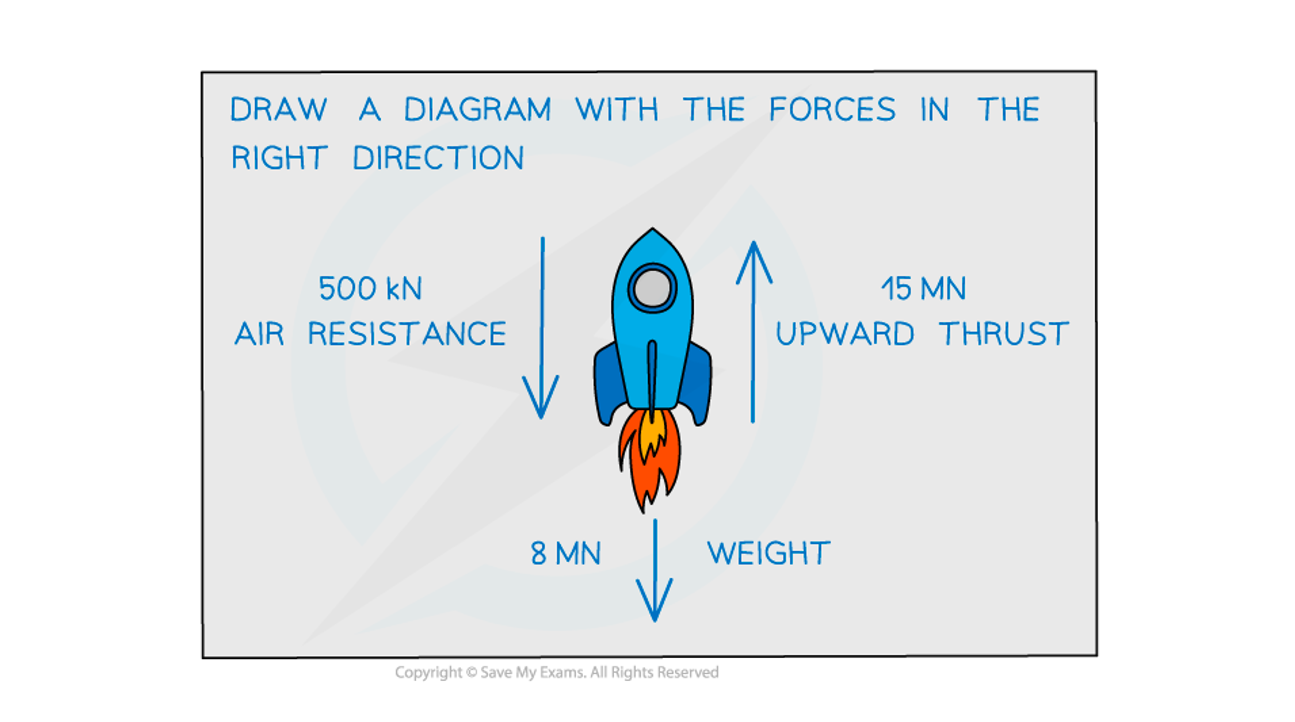
The direction of motion is upwards, therefore upwards is the positive direction
- Air resistance (downward acting), ${\vec{F}}_{f} = - 500 kN = - 500 \times 10^{3} N$
- Weight (downward acting), ${\vec{F}}_{g} = - 8 MN = - 8 \times 10^{6} N$
- Thrust (upward acting), ${\vec{F}}_{t h r u s t} = 15 MN = 15 \times 10^{6} N$

Step 2: Calculate the net external force

${\vec{F}}_{n e t} = (15 \times 10^{6}) + (- 8 \times 10^{6}) + (- 500 \times 10^{3})$

${\vec{F}}_{n e t} = 6.5 \times 10^{6} N = 6.5 MN$

The positive value indicates that the resultant force acts in the direction of motion, i.e. upwards

Step 3: State the equation for Newton's second law

${\vec{a}}_{s y s} = \frac{{\vec{F}}_{n e t}}{m_{s y s}}$

Step 4: Calculate the acceleration and state the direction

$\vec{a} = \frac{6.5 \times 10^{6}}{0.8 \times 10^{5}}$

$\vec{a} = 81 m / s^{2}$ upwards

The answer is therefore C

Worked Example

A car windscreen makes an angle of $30 °$ to the horizontal. The weight of a water drop accelerating down the windscreen is $8.0 \times 10^{- 5} N$ . The normal contact force on the water drop is $F_{N}$ .

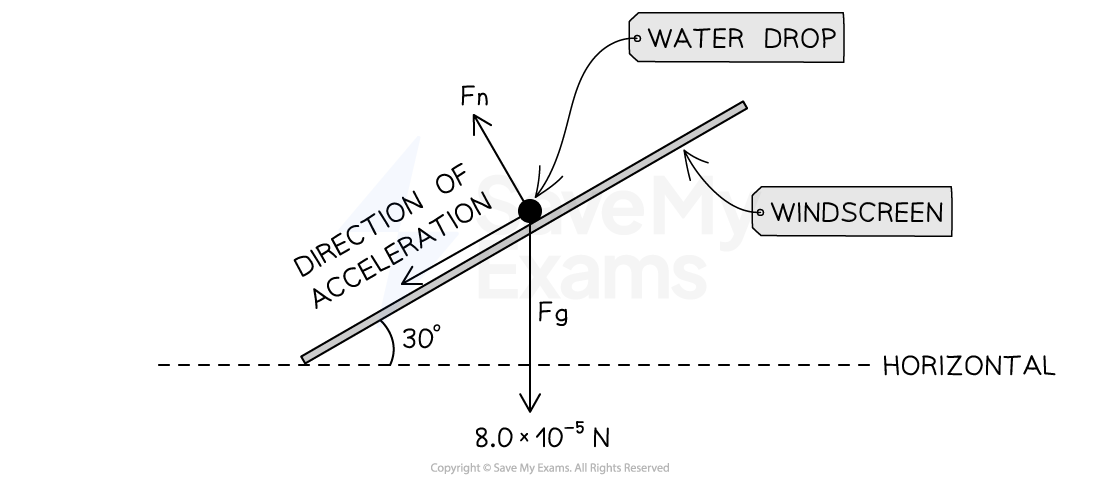
Which of the following shows the correct magnitude of the acceleration of the water drop, assuming that the friction between the windscreen and the drop is negligible?

A $0.05 m / s^{2}$

B $0.8 m / s^{2}$

C $1 m / s^{2}$

D $5 m / s^{2}$

The correct answer is D

Answer:

Step 1: Analyze the scenario

The water drop is accelerating downward, parallel to the line of the slope
- So there is a net external force acting down parallel to the line of the slope
The water drop has no motion perpendicular to the line of the slope
- So there is a zero net external force perpendicular to the line of the slope
Therefore, only the motion of the water drop parallel to the line of the slope should be considered

Step 2: Draw a diagram to show the component acting parallel to the inclined plane

The water drop moves down the windscreen as a result of its weight component parallel to the slope of the windscreen
Draw a diagram to show the correct component

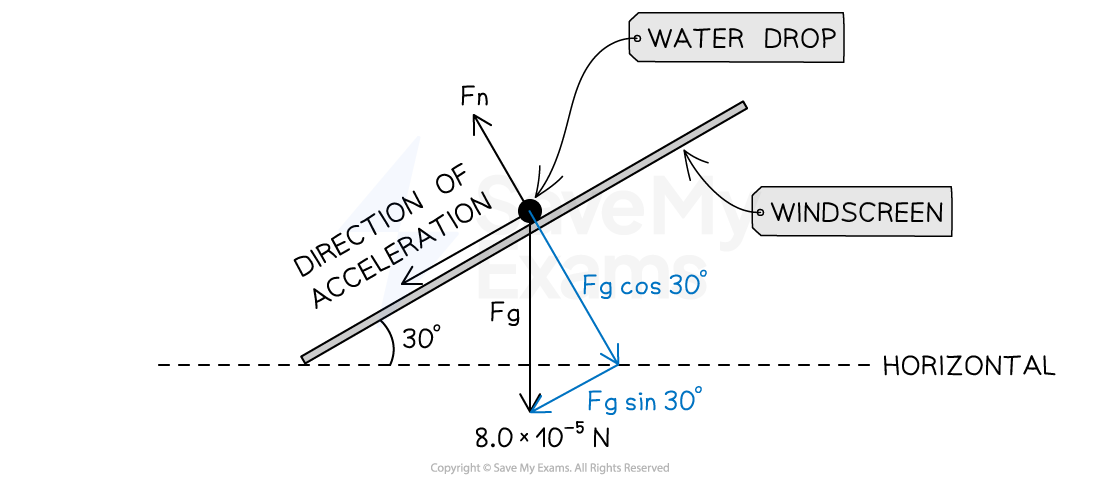
Forces acting on a water drop on a 30-degree inclined windscreen. Forces include weight (Fg), components Fg cos 30° and Fg sin 30°, and reaction force (Fn).

Step 3: Determine the net external force of the water drop moving down the windscreen

${\vec{F}}_{n e t} = {\vec{F}}_{g} \sin (30)$

${\vec{F}}_{n e t} = (8.0 \times 10^{- 5}) (\sin (30))$

${\vec{F}}_{n e t} = 4.0 \times 10^{- 5} N$

Step 4: Determine the mass of the water drop

Recall the equation for calculating the weight of an object

${\vec{F}}_{g} = m g$

Rearrange the equation to make mass, $m$ the subject:

$m = \frac{{\vec{F}}_{g}}{g}$

Calculate the mass of the water drop:

$m = \frac{(8.0 \times 10^{- 5})}{10}$

$m = 8.0 \times 10^{- 6} kg$

Step 5: Calculate the acceleration of the water drop moving down the windscreen

Recall the equation for Newton's second law of motion:

${\vec{a}}_{s y s} = \frac{{\vec{F}}_{n e t}}{m_{s y s}}$

Calculate the acceleration of the water drop:

${\vec{a}}_{s y s} = \frac{(4.0 \times 10^{- 5})}{(8.0 \times 10^{- 6})}$

${\vec{a}}_{s y s} = 5 m / s^{2}$

The answer is therefore D

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Next topic

Did this page help you?

Newton's Second Law (College Board AP® Physics 1: Algebra-Based)

Study Guide

Newton's second law

Mass and net external force

Newton's second law in two dimensions

Worked Example

Worked Example

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Ann Howell