Newton's Law of Gravitation (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself

Author

Ann Howell

Expertise

Physics Content Creator

Newton's law of gravitation equation

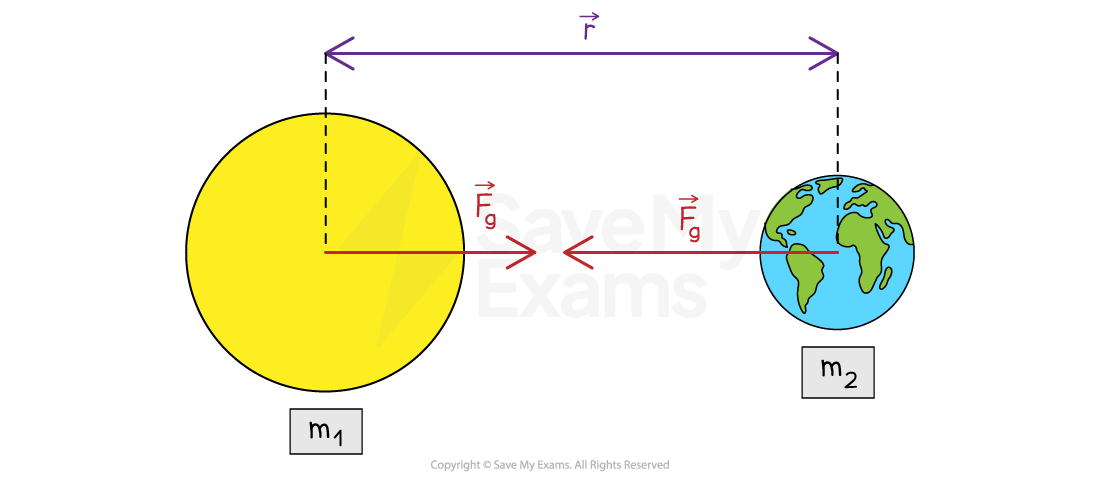
Newton’s law of universal gravitation describes the gravitational force between two objects or systems as:
- directly proportional to each of their masses
- inversely proportional to the square of the distance between the systems’ centers of mass
Newton's law of universal gravitation applies between two bodies when outside a uniform gravitational field
- For example, between the Earth and the Sun or the Earth and the Moon
Although planets are not point masses, their separation is much larger than their radius
- Therefore, Newton’s law of gravitation applies to planets orbiting the Sun
Recall that the mass of a uniform sphere can be considered to be a point mass at its centre
- So the gravitational field around a uniform sphere is identical to that around a point mass

The equation for Newton's law of universal gravitation is given by:
$|\vec{F_{g}}| = G \frac{m_{1} m_{2}}{r^{2}}$
Where:
- $|\vec{F_{g}}| =$ magnitude of the gravitational force between the two objects, measured in $N$
- $G =$ universal gravitational constant = $6.67 \times 10^{- 11} N \cdot m^{2} / {kg}^{2}$
- $m_{1} =$ mass of object 1, measured in $kg$
- $m_{2} =$ mass of object 2, measured in $kg$
- $r =$ the distance between the centres of mass of the two objects, measured in $m$

Quantities in Newton's law of universal gravitation

Diagram showing gravitational force (Fg) between two masses, m1 and m2, at distance r. Arrows indicate the forces toward each other. — **Newton's law of universal gravitation says that the gravitational force Fg is equal to G times the mass of both objects m1 and m2 divided by the square of the distance between the centres of mass r**

The $F_{g} \propto \frac{1}{r^{2}}$ relation is called the ‘inverse square law’
- This means that when the distance between masses is doubled, the gravitational force between the objects reduces by ${(\frac{1}{2})}^{2} = \frac{1}{4}$

Worked Example

A satellite of mass 6500 kg is orbiting the Earth at 2000 km above the Earth's surface. The gravitational force between them is 37 kN.

Which of the following is the mass of the Earth? The radius of the Earth is 6400 km.

A $6.02 \times 10^{18} kg$

B $3.41 \times 10^{23} kg$

C $3.50 \times 10^{24} kg$

D $6.02 \times 10^{24} kg$

The correct answer is D

Answer:

Step 1: Analyze the scenario

Draw a diagram to show all the known quantities

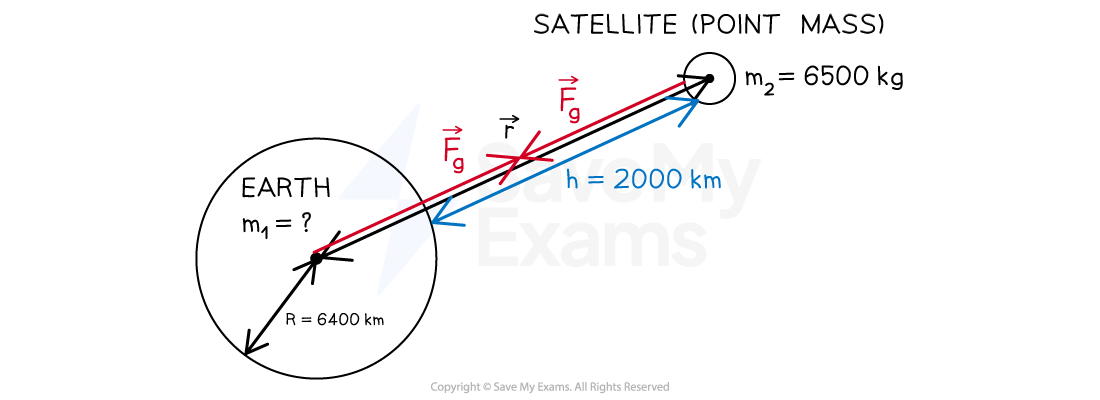
Gravitational forces between Earth and a satellite. Earth’s radius is 6400 km, the distance to the satellite is 2000 km, and m2 equals 6500 kg. The mass of the Earth m1 is unknown.

The object model is used in this scenario
$r$ is the distance between the center of the Earth and the satellite equal to the radius of the Earth $R$ plus the height of orbit of the satellite $h$
- $r = R + h$

Step 2: List the known quantities

Mass of satellite, $m_{2} = 6500 kg$
Height of satellite orbit above the Earths surface, $h = 2000 km = 2 \times 10^{6} m$
Magnitude of gravitational force between Earth and satellite, $|F_{g}| = 37 kN = 37 \times 10^{3} N$
Radius of the Earth, $R = 6400 km = 6.4 \times 10^{6} m$
Universal gravitational constant, $G = 6.67 \times 10^{- 11} m^{3} / (kg \cdot s^{2})$

Step 3: Calculate the distance between the center of the Earth and the satellite $r$

$r = R + h$

$r = (6.4 \times 10^{6}) + (2 \times 10^{6})$

$r = 8.4 \times 10^{6} m$

Step 4: Rearrange the equation for Newton's law of universal gravitation to make the mass of the Earth $m_{1}$ the subject

$|\vec{F_{g}}| = G \frac{m_{1} m_{2}}{r^{2}}$

$|\vec{F_{g}}| \cdot r^{2} = G m_{1} m_{2}$

$\frac{|\vec{F_{g}}| \cdot r^{2}}{G m_{2}} = m_{1}$

Step 5: Substitute the known quantities into the rearranged form of the equation to calculate the mass of the Earth $m_{1}$

$m_{1} = \frac{(37 \times 10^{3}) {(8.4 \times 10^{6})}^{2}}{(6.67 \times 10^{- 11}) \cdot 6500}$

$m_{1} = 6.02 \times 10^{24} kg$

The answer is therefore D

Examiner Tip

A common mistake in exams is to forget to add together the distance from the surface of the planet $h$ and its radius $R$ to obtain the value of r. The distance r is measured from the center of the mass, which is from the center of the planet.

Earth's radius (R) with the center of mass, the height of orbit (h) above Earth’s surface, and the orbital radius (r), calculated as R plus h.

Make sure to square the separation r in the equation!

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Next topic

Did this page help you?