Inertial vs Gravitational Mass (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself

Author

Ann Howell

Expertise

Physics Content Creator

Inertial versus gravitational mass

Inertial mass

Objects have inertial mass, or inertia
- Inertia is a property that determines how much an object’s motion resists changes when interacting with another object
Newton's second law is used to calculate inertial mass

${\vec{a}}_{s y s} = \frac{{\vec{F}}_{n e t}}{m_{s y s}} \to {\vec{F}}_{n e t} = m_{s y s} {\vec{a}}_{s y s}$

Measuring inertial mass

The inertial mass of an object can be determined by applying a force to accelerate the mass
- This is commonly done by setting a mass oscillating on the end of a spring with a spring constant, $k$ , and calculating the time period

Measuring inertial mass using a mass-spring system

A physics experiment setup with a clamp stand, ruler, spring, mass hanger holding a mass, a nail as a marker, and a stopwatch displaying 0.00 seconds. — **Setting a mass on a spring oscillating to measure the time period of oscillating enables the inertial mass to be calculated**

Set the mass oscillating and record the time for 10 oscillations using a stop watch
- One oscillation involves the mass moving up to the top and back down to the bottom
Divide the total time for the 10 oscillations by 10 to obtain the time period
- The time period is the time for one oscillation
Using the equations for centripetal force, angular velocity and time period an equation for the spring constant, $k$ , and the time period is obtained to calculate the inertial mass of the object

$m_{s y s} = \frac{k T^{2}}{2 π}$

Gravitational mass

Gravitational mass is related to the force of attraction between two systems with mass
Newton's law of gravitation is used to calculate the gravitational mass

$|\vec{F_{g}}| = G \frac{m_{1} m_{2}}{r^{2}}$

Measuring gravitational mass

The gravitational mass of an object can be determined by placing the object in a gravitational field and measuring the gravitational force, $F_{g}$ , on the mass
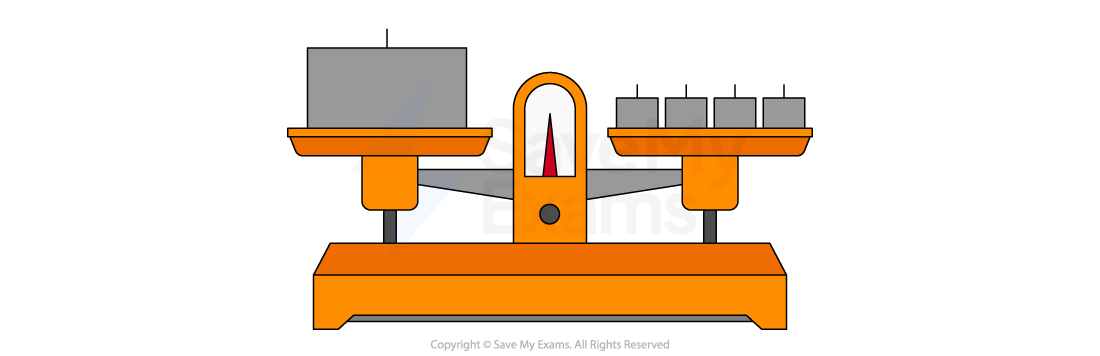
- This is commonly done by balancing the mass on a set of balance scales
- The magnitude of the masses needed for the scales to be balanced (sitting horizontally on the pivot) is equal to the gravitational mass of the object
The balance scales below sit horizontally, showing that four single masses on the right equal the gravitational mass of the object on the left

Measuring gravitational mass using a balance scale

A balance scale with a large grey mass on the left pan and several smaller grey masses on the right pan, illustrating a weight comparison. — **Balancing a mass on a balance scale to measure the magnitude of the mass needed to balance it gives the gravitational mass**

Equivalence principle

Inertial mass and gravitational mass have been experimentally verified to be equivalent
- Using the experimental methods above, the inertial and gravitational masses of an object are found to be the same
Algebraically, this means

${\vec{F}}_{n e t} = m_{s y s} {\vec{a}}_{s y s} = |\vec{F_{g}}| = G \frac{m_{1} m_{2}}{r^{2}}$

$m_{s y s} {\vec{a}}_{s y s} = G \frac{m_{1} m_{2}}{r^{2}}$

So, when $m_{s y s} = m_{1}$

${\vec{a}}_{s y s} = G \frac{m_{2}}{r^{2}}$

Then the object accelerates at the same rate as the magnitude of the gravitational field strength

${\vec{a}}_{s y s} = |\vec{g}|$

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Next topic

Did this page help you?