Translational Equilibrium (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself

Author

Ann Howell

Expertise

Physics Content Creator

Translational equilibrium

Translational equilibrium is defined as

A configuration of forces such that the net force exerted on a system is zero

Stationary object

We know that if there is no net force acting on an object then there is no change in the object's motion
- Therefore a stationary object remains stationary
Vectors can be added together using a vector sum
The force vectors acting on a picture modeled as a hanging object are:
- Tension is the macroscopic net result of forces that segments of the string exert on each other in response to an external force
- The weight exerted on the object by the gravitational field strength, $g$

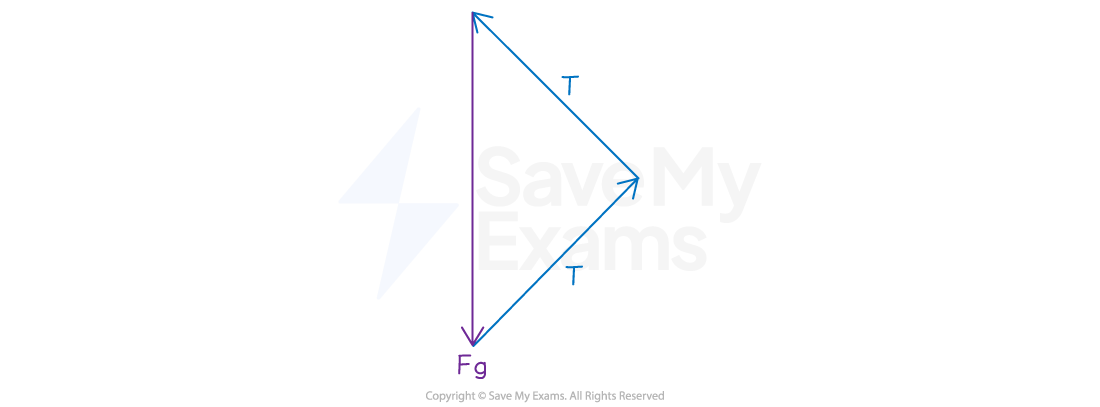
Translational equilibrium of a stationary hanging object

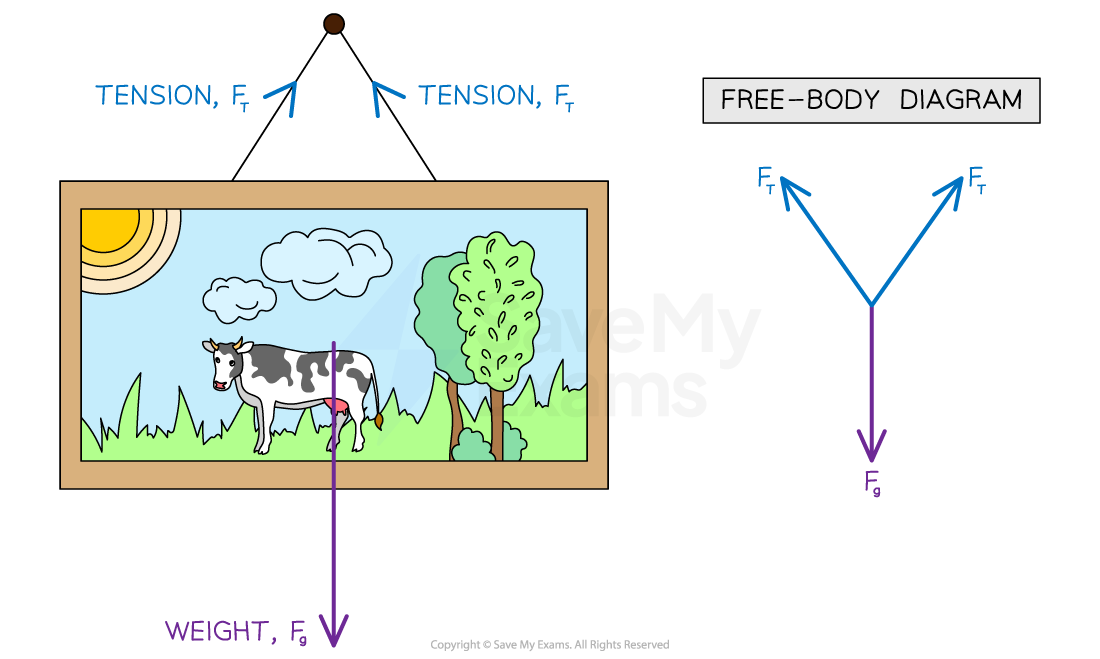
A framed picture of a cow hanging from two cords with equal tension (Ft). The weight (Fg) is balanced by the tensions. Includes a free-body diagram. — **A stationary hanging object is kept in translational equilibrium by tension in the strings and the weight of the picture**

When an object is stationary, the force vectors acting on the object are arranged using the tip-to-tail method so that the vector sum is equal to zero

Force diagram of a stationary hanging object

A triangle with three arrows representing vectors. Two blue vectors labeled "T" form the sides of the triangle and a purple vector labeled "W" points downward. — **When a system is in translational equilibrium the force triangle creates a net force of zero.**

Moving objects

If there is no net force acting on an object, then there is no change in the object's motion
- Therefore, a moving object remains moving at a constant velocity in the same direction
This means the force vectors acting on the object are also arranged using the tip-to-tail method so they combine to equal zero
The force vectors acting on the object are:
- The weight exerted on the object by the acceleration due to gravity, $g$
- The friction exerted on the object due to the interaction between the object and the surface of the slope
- The normal force is the perpendicular component of the force exerted on an object by the surface with which it is in contact; it is directed away from the surface.

Translational equilibrium of a moving object at a constant velocity

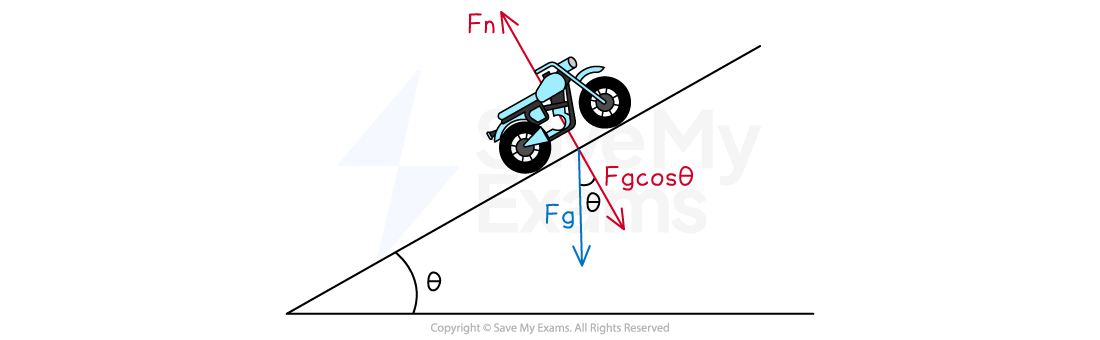
Diagram of a motorcycle on a slope showing force vectors: normal force (Fn) upward, gravity's component (Fg cos θ) downward, and gravity (Fg) vertically. — **An object moving at a constant speed on an inclined plane will also be in translational equilibrium.**

When an object is moving at a constant speed, the force vectors acting on the object are arranged using the tip-to-tail method so that the vector sum is equal to zero

Force diagram of a moving object at a constant velocity

A diagram of three forces with arrows labeled Ff, Fg, and FN forming a right-angle triangle. Ff points upwards, FN points left, and Fg points downwards. — **When a system is in translational equilibrium the force triangle creates a net force of zero.**

Derived equation

A configuration of forces such that the net force exerted on a system is zero

$\sum_{i} \vec{F_{i}} = 0$

Derivation:

Step 1: Identify the fundamental principle

Newton's second law is given by:

${\vec{F}}_{n e t} = m \vec{a}$

Where:
- ${\vec{F}}_{n e t}$ = net force exerted on the system, in $N$
- $m$ = mass of the system, in $kg$
- $\vec{a}$ = acceleration of the system, in $m / s^{2}$

Step 2: Apply the specific conditions

When an object is in transitional equilibrium, it is either at rest or moving with a constant velocity
As there is no change in velocity, acceleration is zero, $\vec{a}$ = 0
The equation for net force becomes:

${\vec{F}}_{n e t} = 0$

To maintain transitional equilibrium, the sum of the forces exerted on the system must equal zero:

${\vec{F}}_{n e t} = {\vec{F}}_{1} + {\vec{F}}_{2} + {\vec{F}}_{3} + . . . + {\vec{F}}_{n} = 0$

$\sum_{i} \vec{F_{i}} = 0$

Worked Example

An object is acted on by three forces one of magnitude 5 N acting downwards, one of magnitude 4 N acting to the right and a third P N acting at an angle to the vertical as shown in the diagram.

Vectors with labeled components: X and 4N pointing right and northeast respectively, intersecting at a point labeled N and S pointing downward from the intersection.

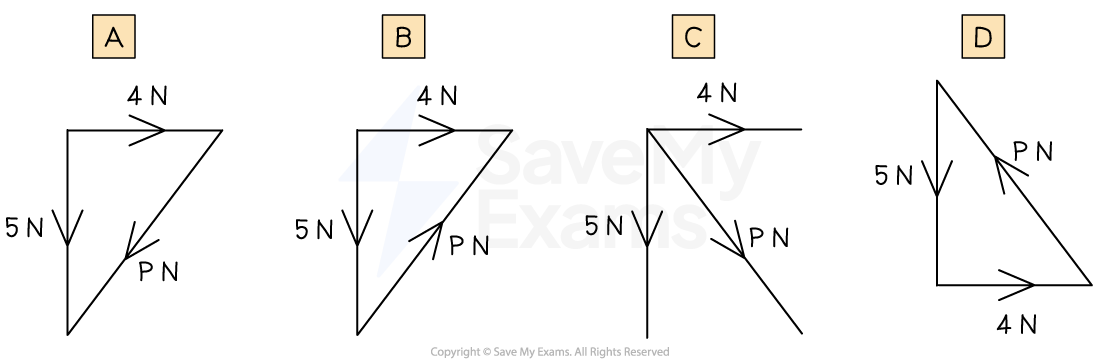
Four diagrams labeled A to D show different arrangements of forces (5N and 4N) on a right-angled triangle, with unknown force X acting in various directions.

Identify the diagram that shows the object is in translational equilibrium.

Answer:

Step 1: Identify properties of a force diagram that show an object in translational equilibrium

An object in translational equilibrium will have a force triangle that shows the force vectors arranged tip to tail

Step 2: Identify the correct answer option

When following the force vectors in a counterclockwise direction from the top point in the force triangle:
- Each arrow is pointing in the counterclockwise direction
Hence this is answer option B

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Next topic

Did this page help you?