Study GuidesExam QuestionsPast Papers
AP®PhysicsCollege BoardPhysics 1: Algebra-BasedStudy GuidesUnit 2: Force & Translational DynamicsForces & Free-Body DiagramsFree Body Diagrams

Free Body Diagrams (College Board AP® Physics 1: Algebra-Based)

Study Guide

Ann Howell

Written by: Ann Howell

Reviewed by: Caroline Carroll

Free-body diagrams

Properties of free-body diagrams

  • Free-body diagrams can be used to:

    • identify which forces act in which plane

    • determine the resultant force 

  • Forces are vector quantities that describe the interactions between objects or systems

  • The free-body diagram of an object or system uses arrows to show each of the forces exerted on the object by the environment

    • The length of the arrow represents the magnitude of the vector

    • The direction of the arrow represents the direction of the vector

    • The length of the arrows must be proportional to their magnitudes

  • Each force arrow is labelled with either:

    • a description of the type of force acting and the objects interacting with clear cause and effect, e.g. the gravitational pull of the Earth on the ball

    • the name of the force, e.g. Weight

    • an appropriate symbol, e.g. F subscript g

Examples of forces exerted on objects

Three objects with forces acting on them: a weight on a spring, a parachutist, and a floating object. Forces include tension, weight, fluid resistance, and buoyancy.
Arrows represent the magnitude and direction of a vector

  • A system is treated as though all of its mass is located at the center of mass

    • The forces exerted on an object or system are represented as vectors originating from their center of mass

Free-body diagram of a suspended object

Two rocks tied with ropes; the left is hanging, and the right illustrates forces with arrows: tension force upwards, weight force downwards.
A free-body diagram of a suspended object shows the forces of tension and weight

Free-body diagram of object moving on rough surface

Forces on a block: left image labeled "Applied Force" with an arrow pushing the block right; right image with arrows indicating "Frictional Force," "Normal (Reaction) Force," and "Weight Force."
A free-body diagram of an object moving on a rough surface includes the frictional force acting in the opposite direction to the applied force

Using a coordinate system

  • A coordinate system simplifies the translation from a free-body diagram to an algebraic representation

  • One plane of the coordinate system is parallel to the direction of acceleration

  • A coordinate system consists of:

    • two axes perpendicular to each other

    • a positive direction that is opposite to the negative direction

A coordinate system applied to an object moving on a rough surface

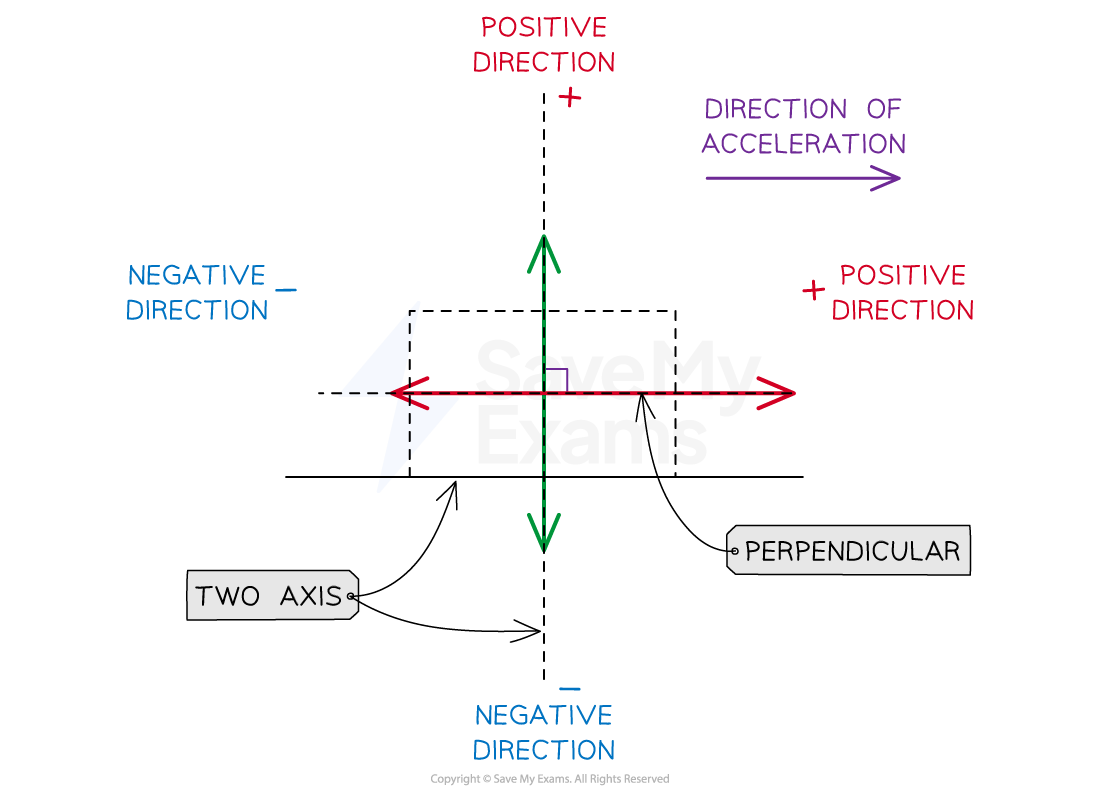
Coordinate system showing red and green arrows indicating positive and negative directions on the axes, with annotations marking directions and acceleration.
A coordinate system helps translate a force diagram into an algebraic representation

  • It is common for the x and y axes to form part of the coordinate system

  • Using a coordinate system is a useful way to measure the angles of forces

    • Angles can be measured from either axis

    • This is explained in the revision note Combining vectors

A coordinate system applied to an object with a force at an angle

A vector diagram showing vector A with components Ax and Ay, making an angle theta with the x-axis. Text indicates the angle is measured from the x-axis.
The angle of resultant vector A is measured from the vector Ax parallel to the x-axis.

Inclined Planes

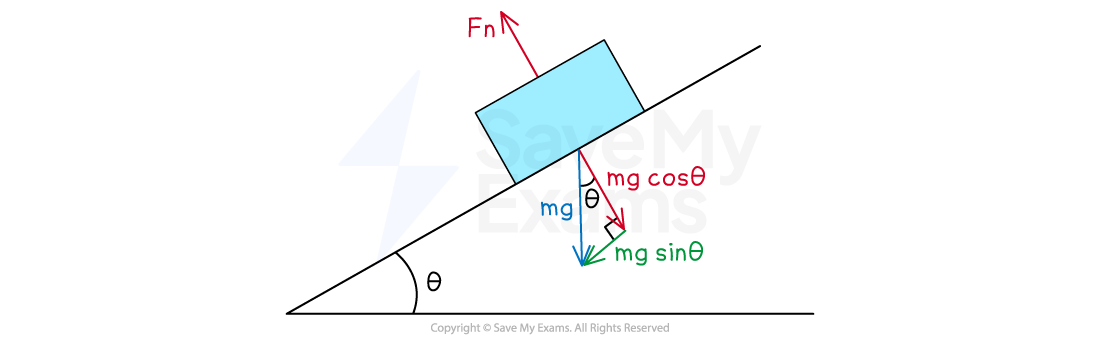
  • In a free-body diagram of an object on an inclined plane, it is useful to set one axis parallel to the surface of the incline

    • An inclined plane, or a slope, is a flat surface tilted at an angle, theta

  • The angles of each of the vectors can then be measured from the inclined plane and the magnitude resolved

    • Instead of thinking of the component of the forces as horizontal and vertical, it is easier to think of them as parallel or perpendicular to the slope

  • The weight F subscript g of the object acts vertically downwards and the normal (or reaction) force, F subscript n always acts vertically upwards from the object on the slope

  • The normal (or reaction) force, F subscript n always acts upwards perpendicular to the slope

    • Remember the equation for weight

F subscript g space equals space m g

  • The weight force, F subscript g, is a vector and can be split into the following components:

    • F subscript g cos open parentheses theta close parentheses perpendicular to the slope

    • F subscript g sin open parentheses theta close parenthesesparallel to the slope

  • If there is no friction, the force F subscript n sin open parentheses theta close parentheses causes the object to move down the slope

  • If the object is not moving perpendicular to the slope, the normal force will be F subscript n space equals space F subscript g cos open parentheses theta close parentheses

Forces on inclined planes

A block on an inclined plane with forces labeled: Fn (normal), mg (gravity), mg cos(theta), and mg sin(theta). Angle theta is shown at the base.
The weight vector of an object on an inclined plane can be split into its components parallel and perpendicular to the slope

Worked Example

Draw free-body diagrams for the following scenarios:

(A) A box being pulled up a slope by a mass on a pulley (resolving the weight into parallel and perpendicular directions)

(B) A man fishing in a stationary boat

(C) A car accelerating along a road

Answer:

Part (A)

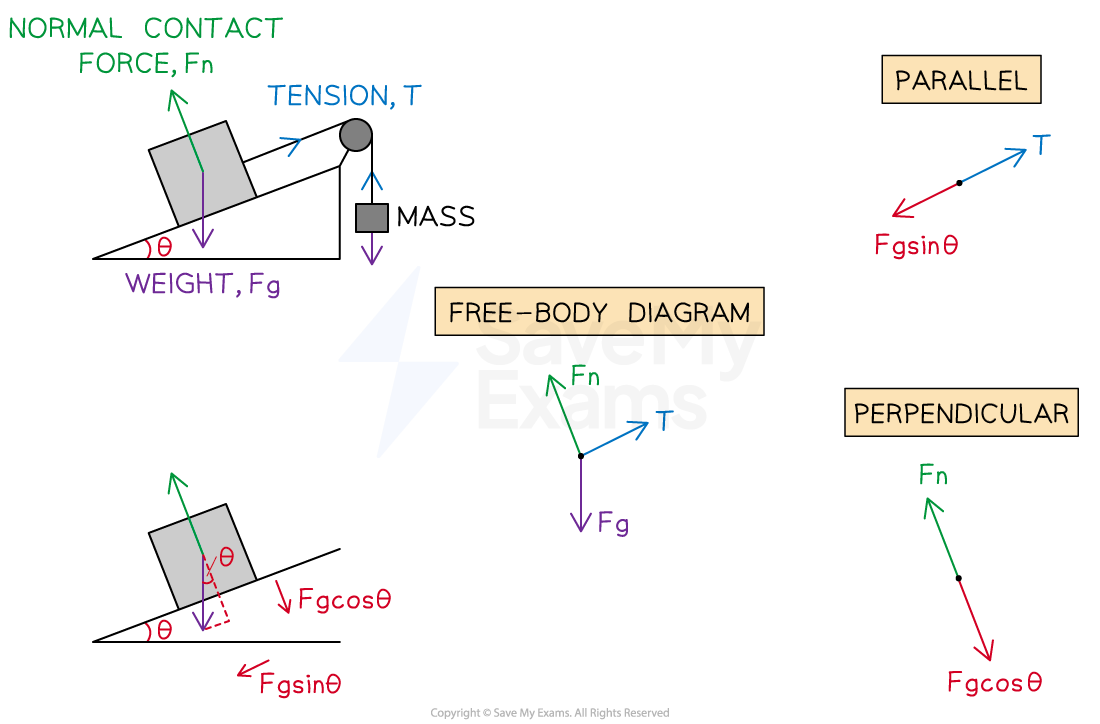
Diagram showing forces on a mass on an inclined plane with tension, normal force, and weight components. Free-body diagram and force components (parallel, perpendicular) included.

  • In problems such as this, it is best to resolve the forces parallel and perpendicular to the slope

Part (B)

A person fishing from a boat, with arrows indicating weight (Fg) downward and upthrust (U) upward. A free-body diagram shows the same vectors separately.

  • As the boat is not moving in the vertical plane, the length of both arrows must be the same, showing forces of equal magnitude

Part (C)

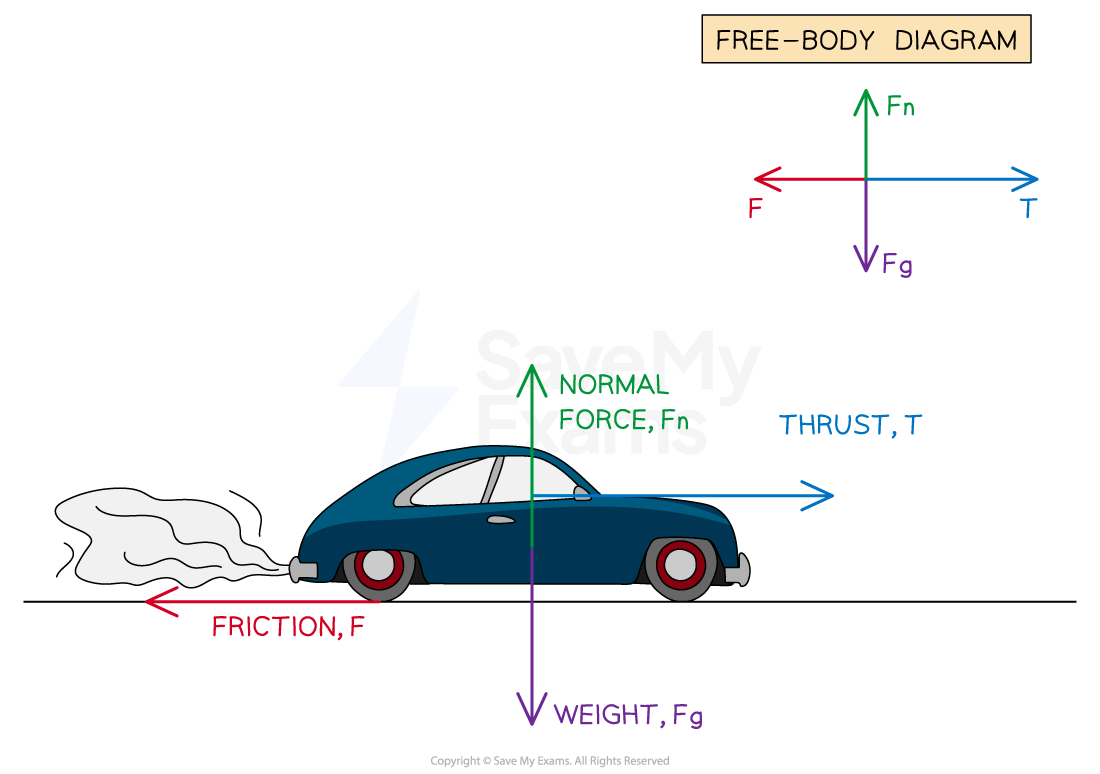
Diagram of a car showing forces acting on it: thrust (T) right, friction (F) left, normal force (Fn) up, and weight (Fg) down. Free-body diagram of forces included.

  • As the car is accelerating, the size of the thrust must be larger than the size of the friction force

  • As in part (c), the upwards and downwards forces must be of equal magnitude

Examiner Tips and Tricks

Make sure you:

  • consider all forces involved in a situation

  • draw forces as vectors

  • draw force vectors to the correct size and to scale

Last updated:

You've read 0 of your 5 free study guides this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Center of MassNext:Forces as Interactions
    Author
    Reviewer
    Ann Howell

    Author: Ann Howell

    Expertise: Physics Content Creator

    Ann obtained her Maths and Physics degree from the University of Bath before completing her PGCE in Science and Maths teaching. She spent ten years teaching Maths and Physics to wonderful students from all around the world whilst living in China, Ethiopia and Nepal. Now based in beautiful Devon she is thrilled to be creating awesome Physics resources to make Physics more accessible and understandable for all students, no matter their schooling or background.

    Caroline Carroll

    Author: Caroline Carroll

    Expertise: Physics Subject Lead

    Caroline graduated from the University of Nottingham with a degree in Chemistry and Molecular Physics. She spent several years working as an Industrial Chemist in the automotive industry before retraining to teach. Caroline has over 12 years of experience teaching GCSE and A-level chemistry and physics. She is passionate about creating high-quality resources to help students achieve their full potential.