Uniform Circular Motion (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself

Author

Ann Howell

Expertise

Physics Content Creator

Period and frequency of uniform circular motion

An object traveling in a circular path at a constant linear speed is traveling in uniform circular motion
- The revolution of an object traveling in a circular path at a constant linear speed can be described using period and frequency
The time to complete one full circular path, one full rotation, or a full cycle of oscillatory motion is defined as period, $T$
The rate at which an object is completing revolutions is defined as frequency, $f$
The equation linking period and frequency is:

$T = \frac{1}{f}$

Where:
- $T$ = period, measured in $s$
- $f$ = frequency, measured in $Hz$
For an object traveling at a constant linear speed, $v$ , in a circular path, the period is given by the equation

$T = \frac{2 π r}{v}$

Where:
- $T$ = period, measured in $s$
- $r$ = radius, measured in $m$
- $v$ = object's linear speed, measured in $m / s$
The linear speed is tangential to the circle of motion
- Linear speed always acts at right angles to the radius of the circle

Linear speed and radius in uniform circular motion

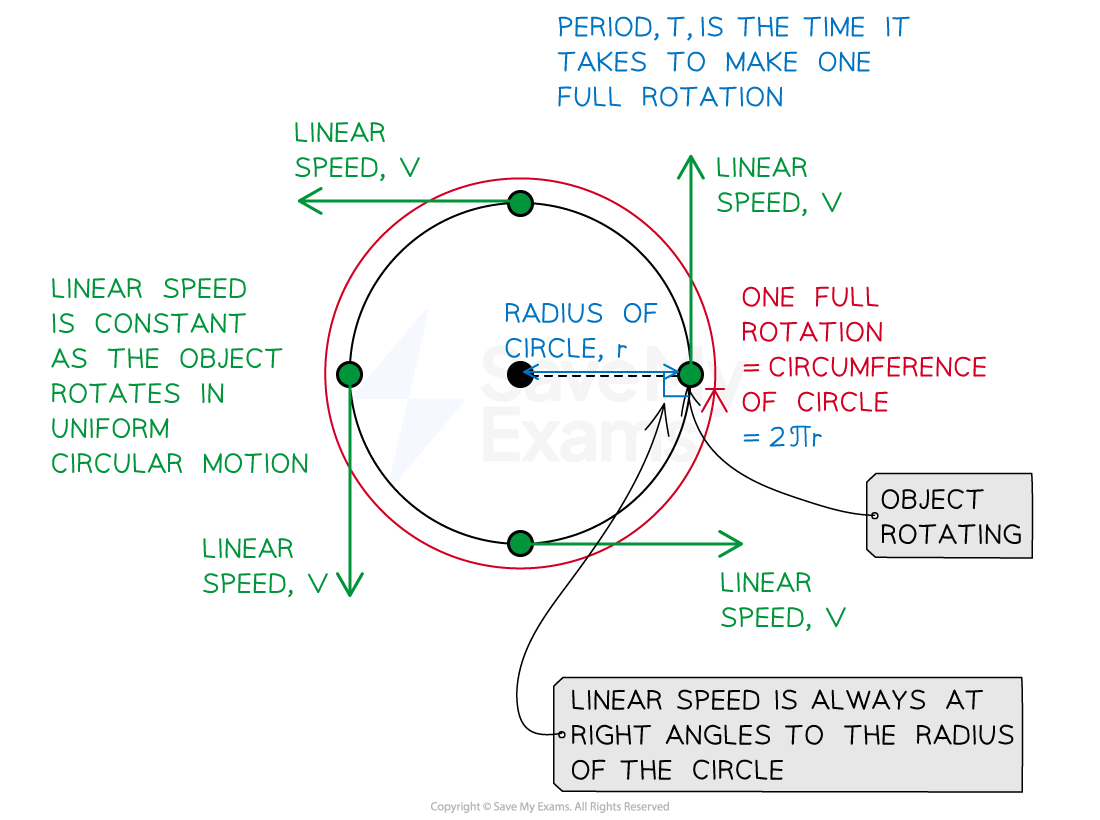
Diagram illustrating uniform circular motion, showing constant linear speed 'v' at different positions around the circle, with radius 'r' and circumference formula 2πr. — **An object rotating in uniform circular motion completes one revolution of the circumference of the circle in period T**

Derived equation

For an object traveling at a constant linear speed, $v$ , in a circular path, the period is given by the equation

$T = \frac{2 πr}{v}$

Derivation:

Step 1: Identify the fundamental principle

The equation linking period and frequency is given by

$T = \frac{1}{f}$

Where:
- $T$ = period, measured in $s$
- $f$ = frequency, measured in $Hz$

Step 2: Apply the specific conditions

The frequency of an oscillation dictates the number of oscillations in a certain time period
The equation linking period and frequency means there is one oscillation in period $T$
In circular motion, one oscillation covers the distance of the circumference of the circle
- The circumference of a circle of radius, $r$ , is given by the equation

$circumference of circle = 2 π r$

Average speed is calculated using the equation

$average speed = \frac{total distance traveled}{total time taken}$

So the linear speed, $v$ , is given by the equation

$v = \frac{2 πr}{T}$

Where
- linear speed, $v$ , is equivalent to average speed, measured in $m / s$
- the circumference of a circle is equivalent to total distance traveled, measured in $m$
- period is equivalent to total time taken, measured in $s$
Rearrange to make period, $T$ , the subject
- Multiply both sides by $T$
$v \cdot T = \frac{2 πr}{T} \cdot T$
- Cancel out the common $T$ 's
$v \cdot T = \frac{2 πr}{T} \cdot T$
- Divide by $v$ on both sides
$\frac{v \cdot T}{v} = \frac{2 πr}{v}$
- Cancel out the common $v$ 's
$\frac{v \cdot T}{v} = \frac{2 πr}{v}$
- Obtain the derived equation for period, $T$

$T = \frac{2 πr}{v}$

Worked Example

The London Eye is a giant Ferris wheel in the city of London that was built as part of the millennium celebrations it rotates slow enough so people on board can observe what is happening in the city below. The radius of the London Eye is 67.5 m and it takes 30 minutes to complete one full rotation.

Which of the following is the linear speed of the London Eye?

A $0.24 m / s$

B $0.47 m / s$

C $14.13 m / s$

D $848 m / s$

The correct answer is A

Answer:

Step 1: List the known quantities

Radius of London Eye, $r = 67.5 m$
Period of rotation, $T = 30 minutes = 30 \cdot 60 = 1800 s$

Step 2: Substitute the known quantities into the equation for linear speed

$v = \frac{2 πr}{T}$

$v = \frac{2 π (67.5)}{1800}$

$v = 0.24 m / s$

The answer is therefore A

Examiner Tip

An object in uniform circular motion travels at a constant linear speed but at a changing linear velocity, $\vec{v}$ . This is because the direction of motion is constantly changing.

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Next topic

Did this page help you?