Circular Motion in a Vertical Loop (College Board AP® Physics 1: Algebra-Based)

Circular motion in a vertical loop

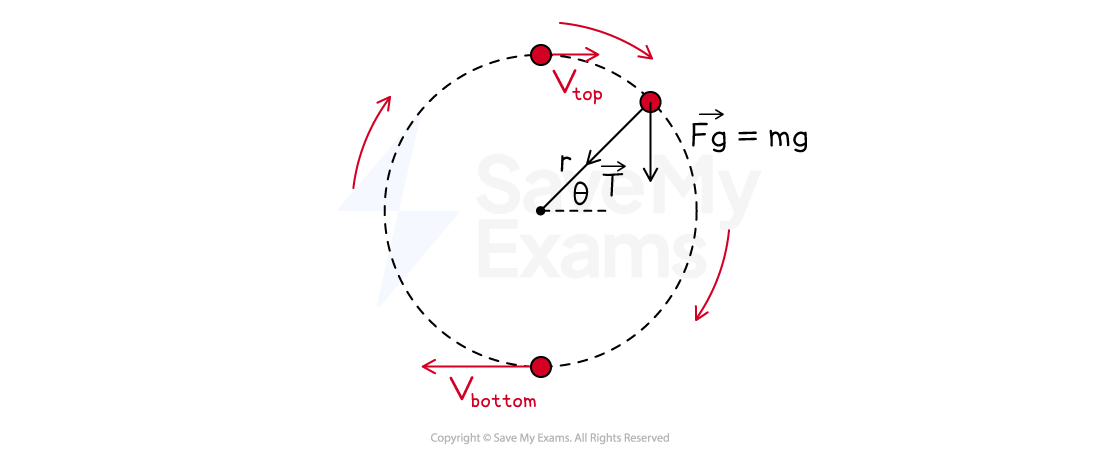
• An object such as a ball on a string is an example of circular motion in a vertical loop

• The forces acting on the ball are:

  • tension in the string

  • gravitational force acting straight downwards

• As the ball moves around the circle:

  • the direction of the tension will change continuously

  • the magnitude of the tension will change continuously, reaching:

    • a maximum value at the bottom

    • a minimum value at the top

• The direction of the gravitational force on the ball never changes

  • Therefore, the resultant centripetal force on the ball changes depending on its position as it rotates around the circle

Forces in a vertical circle

Minimum speed

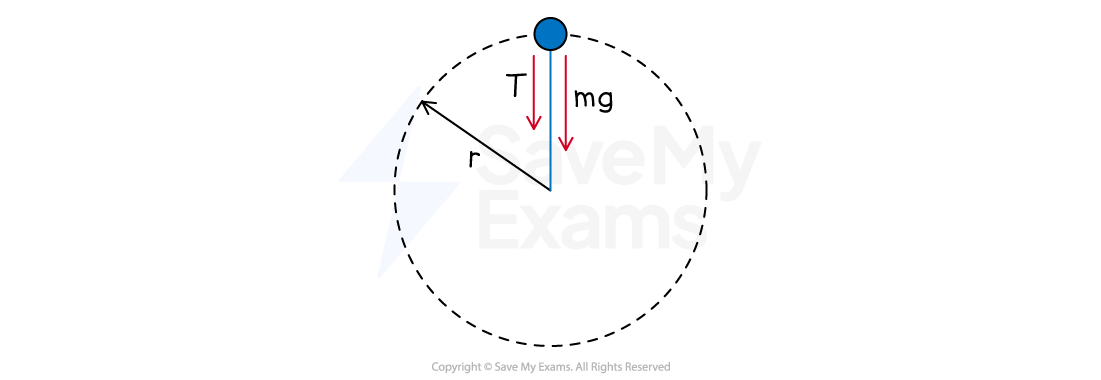
• At the top of a vertical, circular loop, an object requires a minimum speed to maintain circular motion

• The tension in the string is zero at the top of the circular loop

• At the top of the loop at this minimum speed, the gravitational force is the only force that causes the centripetal acceleration

  • So,

Forces at the top of a vertical circle

Derived equation

• The minimum speed required to maintain circular motion at the top of the circular loop is given by:

• Where:

  • minimum speed at the top of the vertical circular loop, measured in

  • acceleration due to gravity at Earth's surface, measured in

  • radius of circle, measured in

Derivation:

Step 1: Identify the fundamental principles

• Newton's second law

• Where:

  • = net centripetal force exerted on the object

  • = mass of the object

  • = centripetal acceleration of the object

• The net force in this case is the gravitational force or the weight force

• The acceleration in this case is the acceleration due to gravity at the Earth's surface

• Therefore:

• Where:

  • = gravitational force exerted on the object

  • = mass of the object

  • = acceleration due to gravity

• The magnitude of the centripetal acceleration of an object moving in a circular path is given by:

• Where:

  • = magnitude of the centripetal acceleration

  • = tangential or linear speed

  • = radius of circular path

Step 2: Apply the specific conditions

• When an object is moving in a circular loop, the net centripetal force is calculated using the tangential speed and the radius of the circular loop

  • Substitute the centripetal acceleration into Newton's second law

• At the top of a vertical circular loop, the gravitational force is the only force that causes the centripetal acceleration

  • The tension in the string is zero

Step 3: Rearrange to obtain an equation for the minimum speed at the top of a vertical circular loop