Circular Motion Examples (College Board AP® Physics 1: Algebra-Based) : Study Guide

Written by: Ann Howell

Reviewed by: Caroline Carroll

Updated on 24 April 2025

Banked surface

A banked surface, normally a road or track is a curved surface where the outer edge is raised higher than the inner edge
- The purpose of this is to make it safer for objects to travel on the curved road at a reasonable speed without skidding
The steeper the banked curve the greater the speed an object can travel around the curve without sliding up or down

Banked surface with friction

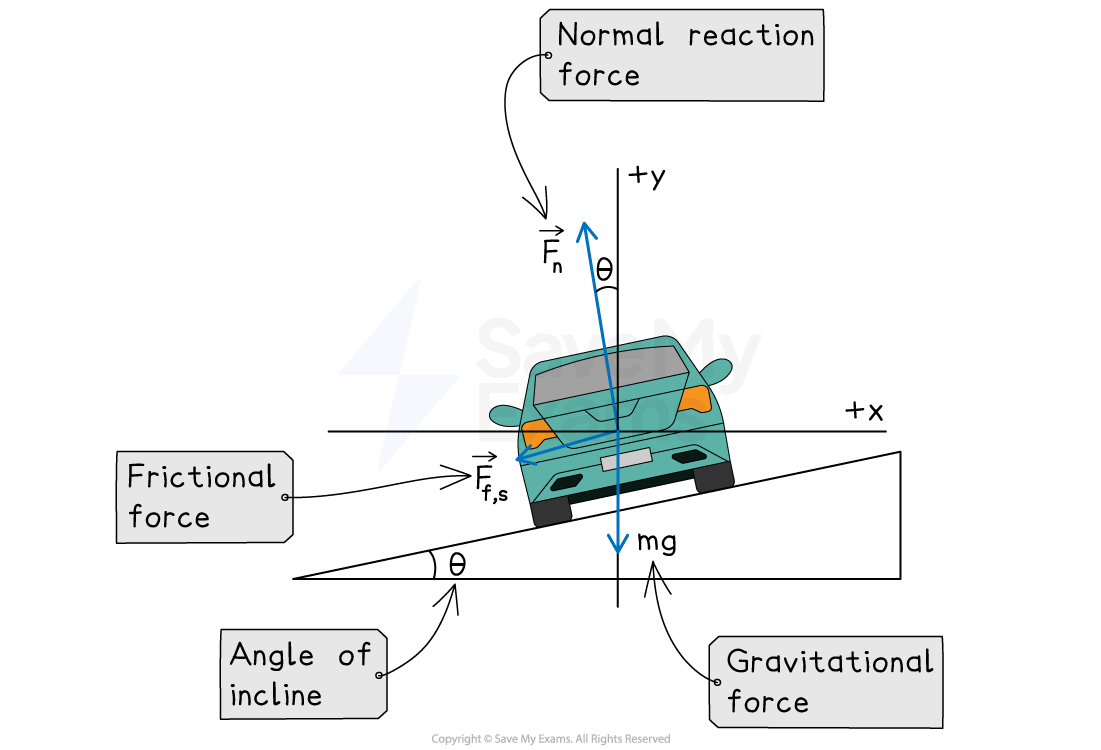
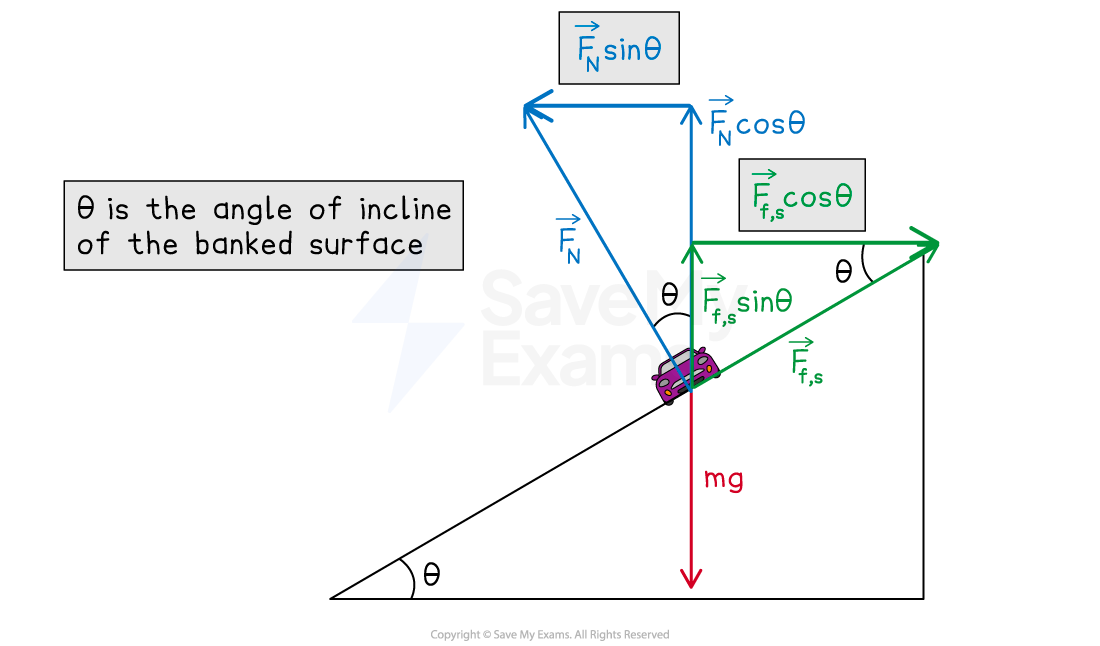
For an object moving on a banked surface with friction:
- gravitational force ${\vec{F}}_{g}$ acts vertically downwards
- normal reaction force ${\vec{F}}_{N}$ acts perpendicular to the surface
- frictional force ${\vec{F}}_{f}$ acts parallel to the surface, either up or down the slope depending on the situation
- centripetal force ${\vec{F}}_{c}$ is the net force acting horizontally towards the center of the circle

Forces acting on an object on a banked surface

A car on an inclined plane, shows forces: gravitational downward, frictional leftward, normal upward, with angle of incline indicated. — **Frictional forces act parallel to and normal forces act perpendicular to the angle of the slope**

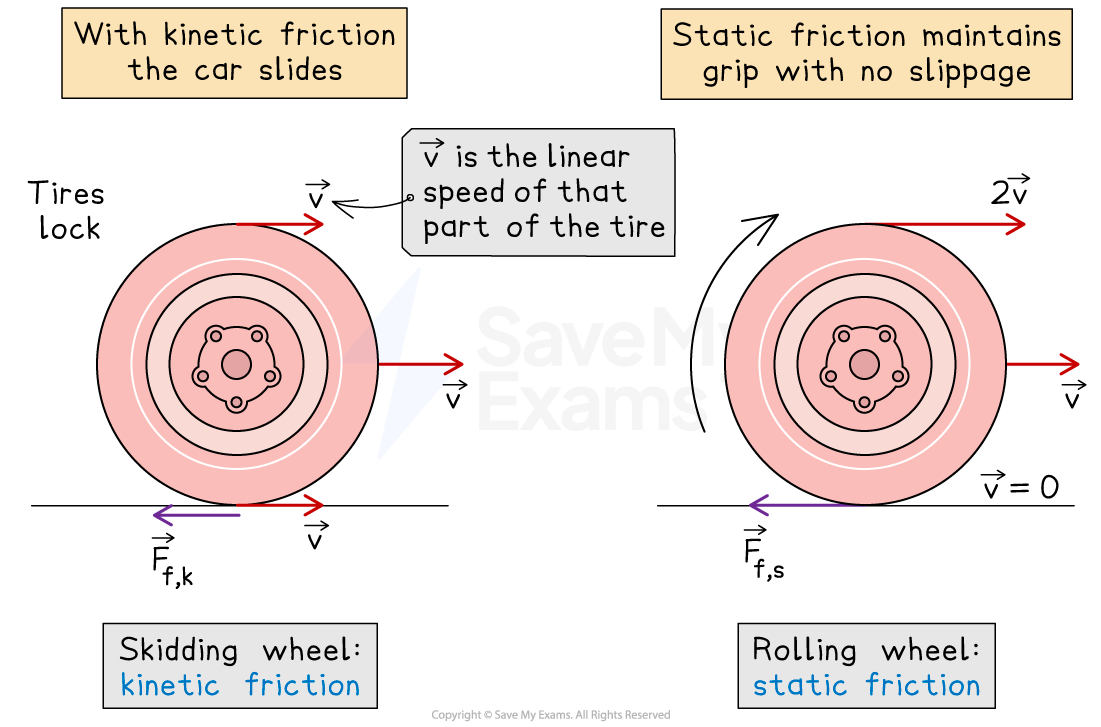
There are two types of friction to consider
- static friction ${\vec{F}}_{f, s}$ prevents the car from skidding
- kinetic friction ${\vec{F}}_{f, k}$ acts if the car starts skidding
If an object remains at the same position up the slope of the banked surface while undergoing uniform circular motion then only static friction is present

Kinetic vs static friction on a tire

Comparision of skidding and rolling wheels. Skidding shows kinetic friction (Fk) opposing wheel movement. Rolling shows static friction (Fs) preventing slippage. — **Kinetic friction acts when the tire is skidding but static friction acts when the tire is rolling**

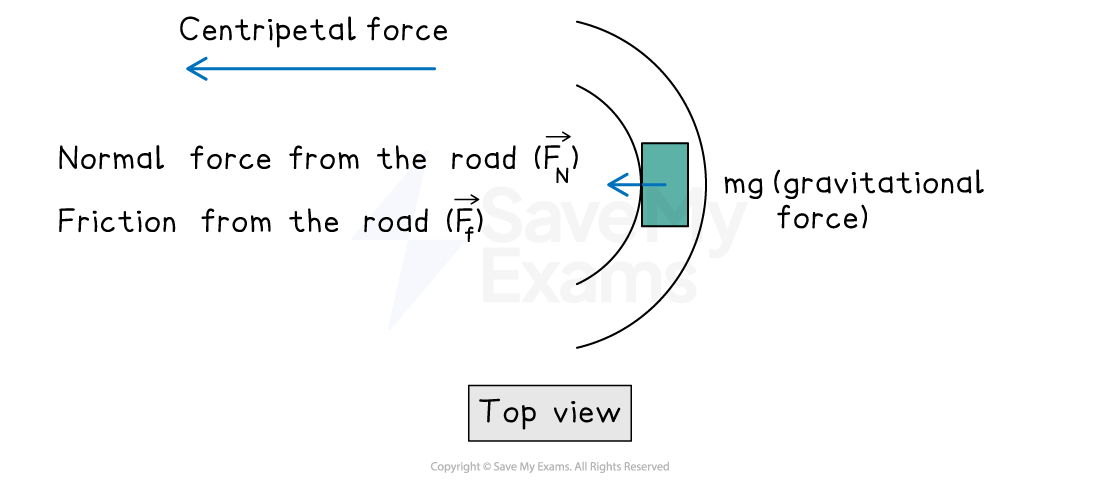
Components of the static friction force and the normal force can contribute to the net centripetal force producing the centripetal acceleration of an object traveling in a circle on a banked surface
- The net centripetal force acts horizontally towards the center of the circle
An object travelling at its ideal speed is travelling at the maximum speed possible before it starts slipping or sliding on the banked surface, and kinetic friction is applied to keep the car in its lane

Net centripetal force

Top view diagram of forces acting on a red rectangle representing a vehicle. Arrows show normal force (n) and friction (fr) from the road and mg (gravity) downward. — **Centripetal force is equal to the horizontal normal force and the frictional force components for an object travelling on a banked surface**

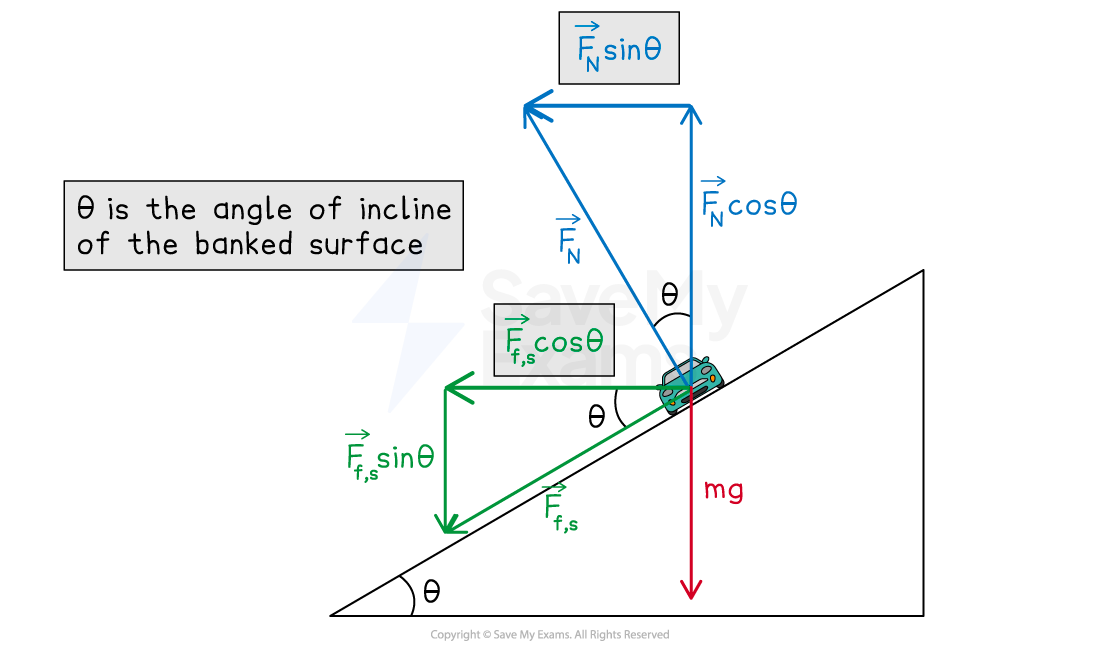
Faster than ideal speed

When the object is moving faster than the ideal speed, static friction acts down the banked surface
- The static friction prevents the object from skidding upward
The net centripetal force is given by the equation

${\vec{F}}_{c} = {\vec{F}}_{N} \sin θ + {\vec{F}}_{f, s} \cos θ$

Where:
- ${\vec{F}}_{c} =$ net centripetal force, measured in $N$
- ${\vec{F}}_{N} =$ normal reaction force, measured in $N$
- $θ =$ angle of incline of banked surface, measured in $°$
- ${\vec{F}}_{f, s} =$ static friction, measured in $N$

Components of forces at faster than ideal speed

Forces on an inclined plane, showing gravitational force (mg) downward, normal force (F_N) perpendicular, and frictional force (F_s) opposing motion. — **The net centripetal force is the horizontal component of static friction and the normal force**

Slower than ideal speed

When the object is moving slower than the ideal speed static friction acts up the banked surface in the opposite direction to the centripetal force
- The static friction prevents the object from skidding downwards
The net centripetal force is given by the equation

${\vec{F}}_{c} = {\vec{F}}_{N} \sin θ - {\vec{F}}_{f, s} \cos θ$

Components of forces at slower than ideal speed

Forces on an inclined plane, showing components: Fs and its components Fs*sinθ and Fs*cosθ in green, FN and its components FN*sinθ and FN*cosθ in blue, and mg in red. — **The net centripetal force is the horizontal component of static friction and the normal force**

Ideally banked surfaces

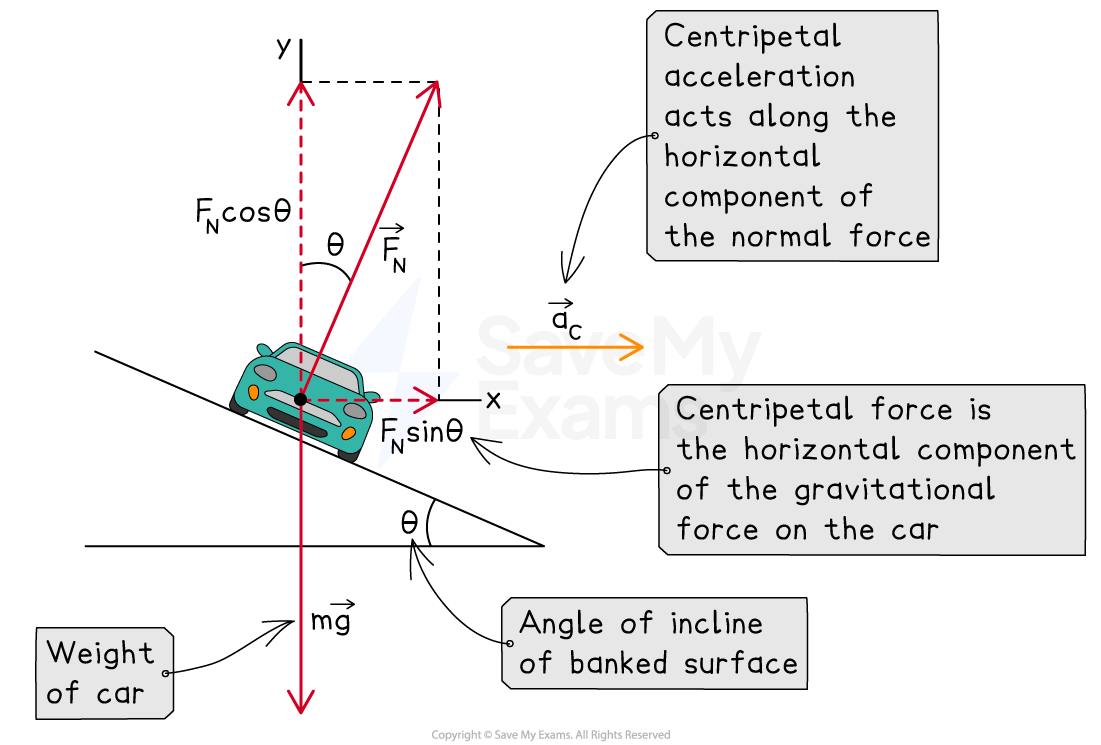
An ideally banked surface has an angle of incline $θ$ so an object can negotiate the curve at a certain speed without the need for friction
For an object moving on an ideally banked surface without friction
- gravitational force ${\vec{F}}_{g}$ acts vertically downwards
- normal reaction force ${\vec{F}}_{N}$ acts perpendicular to the surface
- centripetal force ${\vec{F}}_{c}$ is the net force acting horizontally towards the center of the circle
The net centripetal force is given by the equation

${\vec{F}}_{c} = {\vec{F}}_{N} \sin θ$

Components of the normal force on an ideally banked surface

A car on a sloped road showing forces. Vectors indicate gravity (mg), normal force (FN), and components of the normal force (FN cosθ and FN sinθ), with a labeled angle θ. — **A car on an ideally banked surface remains on a banked surface due to the horizontal component of the normal force**

Worked Example

What is the minimum angle of an ideally banked road so a car can travel at $40 m / s$ and safely negotiate a curve of radius $100 m$ ?

A $0.00 °$

B $0.03 °$

C $2.29 °$

D $58 °$

The correct answer is D

Answer:

Step 1: Analyze the scenario

The car is on an ideally banked road, so there is negligible friction
Therefore, the centripetal force acting towards the center of the curve must be equal to the horizontal component of the normal reaction force of the car

Step 2: List the known quantities

Tangential speed of car, $v = 40 m / s$
Radius of curve, $r = 100 m$
Acceleration due to gravity at Earth's surface, $g = 10 m / s^{2}$

Step 3: Determine an expression for the centripetal force as the horizontal component of the normal force

${\vec{F}}_{c} = {\vec{F}}_{N} \sin θ$

${\vec{F}}_{c} = \frac{m v^{2}}{r}$

${\vec{F}}_{N} \sin θ = \frac{m v^{2}}{r}$ eq (1)

Step 4: Determine an expression for the net zero vertical normal force

${\vec{F}}_{N} \cos θ = m g$ eq (2)

Step 5: Combine equations (1) and (2) to obtain an expression in terms of $θ$ without the normal force, $\vec{F_{N}}$

$\frac{eq (1)}{eq (2)} = \frac{{\vec{F}}_{N} \sin θ}{{\vec{F}}_{N} \cos θ} = \frac{m v^{2}}{r} \cdot \frac{1}{m g}$

$\tan θ = \frac{v^{2}}{g r}$

Step 6: Substitute in the known quantities to obtain the minimum angle of the ideally banked road

$θ = \tan^{- 1} (\frac{v^{2}}{g r})$

$θ = \tan^{- 1} (\frac{40^{2}}{10 \cdot 100})$

$θ = 58 °$

The answer is therefore D

Examiner Tips and Tricks

The value of ${\vec{F}}_{N}$ is not equal to the gravitational force, $m g$ , of the car so it cannot be calculated without the angle of the incline.

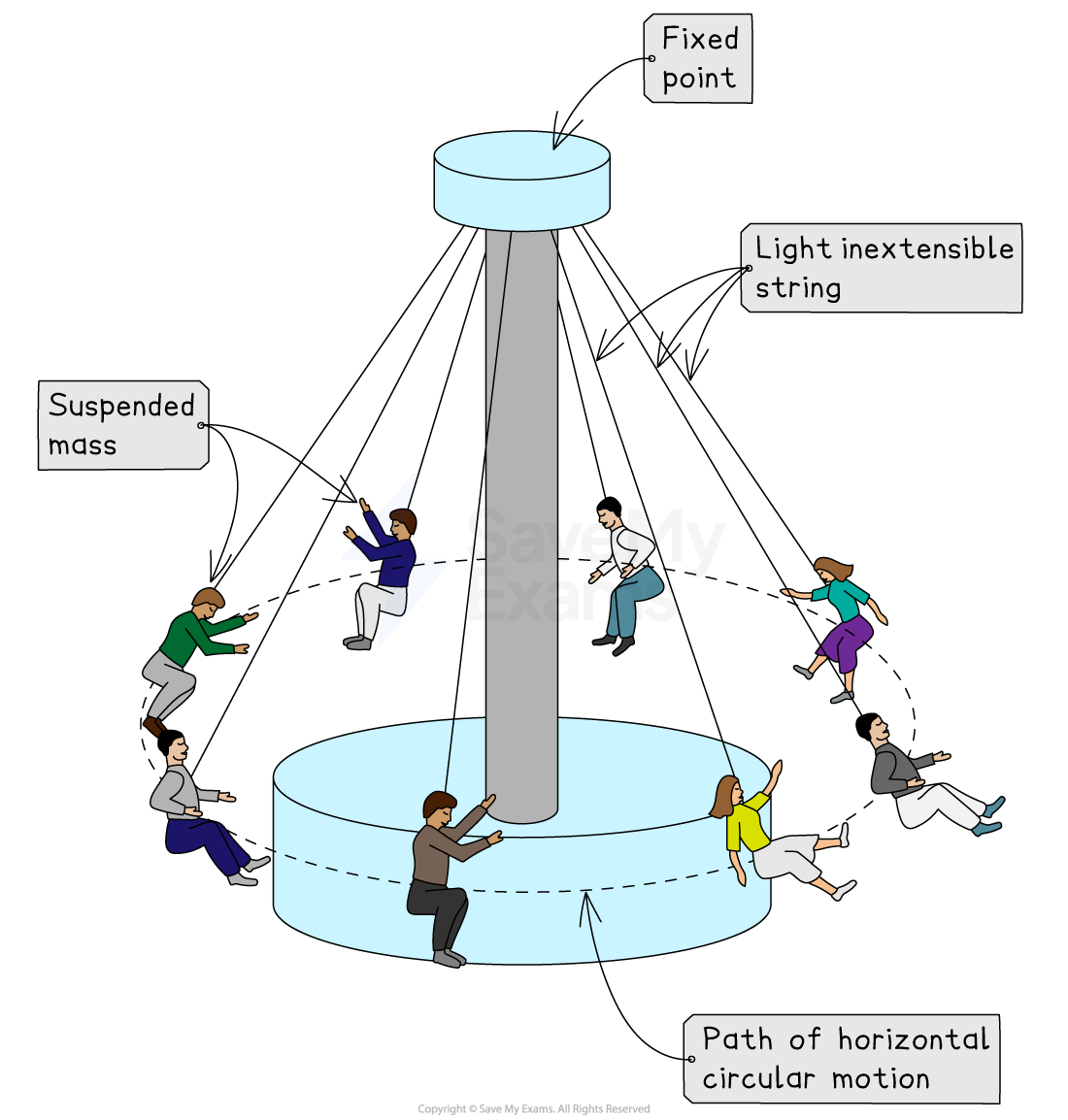
Conical pendulum

A conical pendulum consists of a mass set in horizontal circular motion suspended on the end of a light inextensible string fixed from a central point above
- For example, a fairground ride or a ball suspended on a string

Conical pendulum example

Eight people are seated on swings attached to a central pole, which rotates to lift and spin the riders in the air. The swing ride creates a circular motion. — **This fairground ride is an example of a conical pendulum where the passengers are suspended from a fixed point and undergo horizontal circular motion**

It is assumed that:
- the string is massless
- the string cannot be stretched
- air resistance is negligible
The behavior of a conical pendulum is similar to that of an object on an ideally banked surface where there is no friction
- The normal reaction force of the banked surface on the object is equivalent to the tension in the string
A component of tension contributes to the net force producing centripetal acceleration experienced by a conical pendulum
- The tension in the string and the gravitational force on the mass are not equal, so the mass is not in equilibrium, hence there is centripetal acceleration
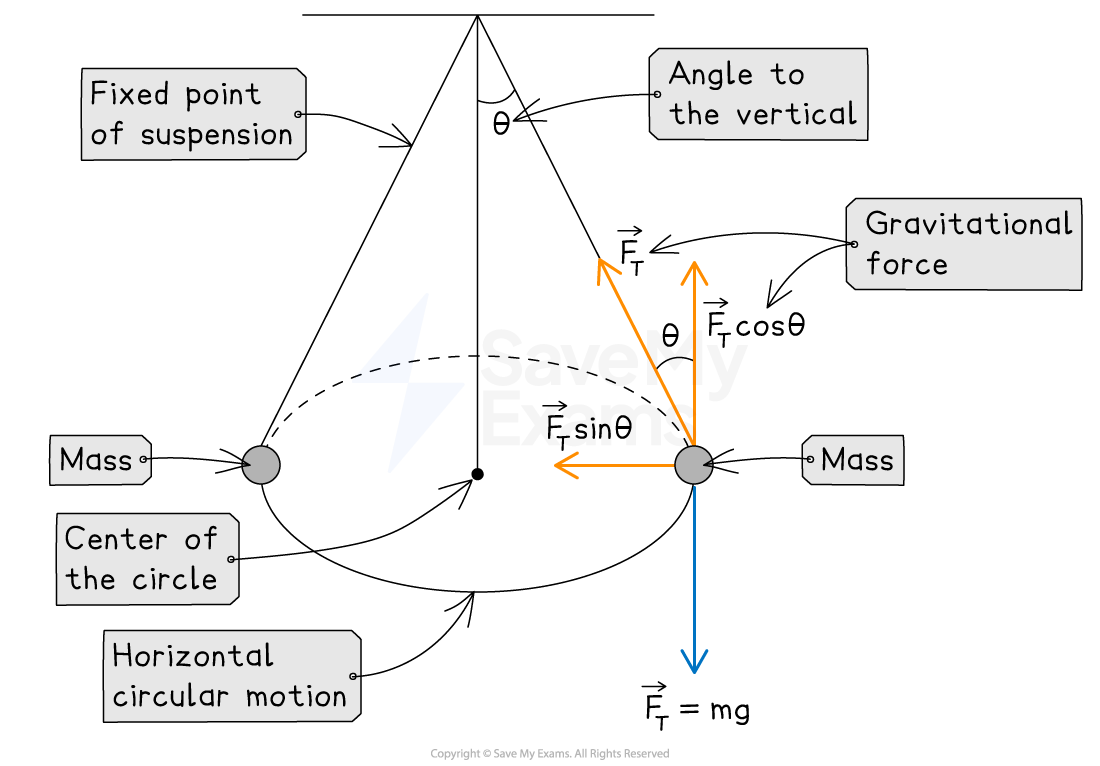
A conical pendulum experiences the following forces:
- gravitational force ${\vec{F}}_{g}$ acting vertically downwards
- tension force ${\vec{F}}_{T}$ acting along the line of the string at an angle $θ$ to the vertical
- centripetal force ${\vec{F}}_{c}$ is the net force acting horizontally towards the center of the circle
The horizontal net centripetal force is given by the equation:

${\vec{F}}_{c} = {\vec{F}}_{T} \sin θ$

The vertical component of the tension in the string is equal to the gravitational force acting on the mass

${\vec{F}}_{g} = m g = {\vec{F}}_{T} \cos θ$

Components of the tension force on a conical pendulum

A pendulum showing forces: tension (F_T) acting at an angle θ, with its components F_T cos θ (vertical) and F_T sin θ (horizontal), and weight (F_g = mg) acting downward. — **The tension component in the string can be resolved horizontally to calculate the net centripetal force acting on the mass**

Worked Example

A conical pendulum has a mass $m$ suspended from a height $h$ by a light inextensible string with tension ${\vec{F}}_{T}$ at an angle of $θ$ to the vertical. It moves in uniform circular motion of radius, $r$ with tangential velocity, $v$ .

A conical pendulum with a mass m has forces T (tension), mg (gravity), angle θ, radius r, string length l, and height h with circular trajectory.

Verify that the time period of the oscillation of the conical pendulum is given by the equation

$T = 2 π \sqrt{\frac{h}{g}}$

Answer:

Step 1: Analyze the scenario and determine the required equations

The following forces are present on a conical pendulum system
- The gravitational force acting on the mass $m$ is $\vec{F_{g}} = m g$
- The vertical component of tension in the string is $\vec{F_{g}} = {\vec{F}}_{T} \cos θ$
- The horizontal component of the tension in the string is $\vec{F_{c}} = {\vec{F}}_{T} \sin θ$
- The centripetal force is given by the equation $\vec{F_{c}} = \frac{m v^{2}}{r}$
- The time period is calculated using $T = \frac{circumference}{tangential speed} = \frac{2 π r}{v}$

Step 2: Determine an expression for the centripetal force as the horizontal component of the tension force

${\vec{F}}_{T} \sin θ = \frac{m v^{2}}{r}$ eq (1)

Step 3: Determine an expression for the net zero vertical tension force

${\vec{F}}_{T} \cos θ = m g$ eq (2)

Step 5: Combine equations (1) and (2) to obtain an expression in terms of $θ$ without the tension force, $\vec{F_{T}}$

$\frac{eq (1)}{eq (2)} = \frac{{\vec{F}}_{T} \sin θ}{{\vec{F}}_{T} \cos θ} = \frac{m v^{2}}{r} \cdot \frac{1}{m g}$

$\tan θ = \frac{v^{2}}{g r}$

$v = \sqrt{g r \tan θ}$

Step 6: Determine an expression for $\tan θ$ in terms of $h$ and $r$

$\tan θ = \frac{opposite}{adjacent} = \frac{r}{h}$

Step 7: Combine the equations to obtain an expression for $v$ in terms of $g$ , $h$ and $r$

$v = \sqrt{g r \cdot (\frac{r}{h})}$

$v = \sqrt{\frac{g r^{2}}{h}}$

$v = r \sqrt{\frac{g}{h}}$

Step 8: Substitute the expression for $v$ into the time period equation

$T = \frac{2 π r}{v}$

$T = 2 π r \div (r \sqrt{\frac{g}{h}})$

$T = 2 π \sqrt{\frac{h}{g}}$ as required

You've read 0 of your 5 free study guides this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself

Did this page help you?

Previous:Circular Motion in a Vertical LoopNext:Kepler's Third Law

Circular Motion Examples (College Board AP® Physics 1: Algebra-Based) : Study Guide

Banked surface

Banked surface with friction

Forces acting on an object on a banked surface

Kinetic vs static friction on a tire

Net centripetal force

Faster than ideal speed

Components of forces at faster than ideal speed

Slower than ideal speed

Components of forces at slower than ideal speed

Ideally banked surfaces

Components of the normal force on an ideally banked surface

Conical pendulum

Conical pendulum example

Components of the tension force on a conical pendulum

You've read 0 of your 5 free study guides this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Unit 1: Kinematics

Scalars & Vectors

Scalar & Vector Quantities

Combining Vectors

Displacement, Velocity & Acceleration

Displacement

Velocity

Acceleration

Representing Motion

Kinematic Equations

Motion Graphs

Reference Frames & Relative Motion

Vectors & Motion

Vectors & Motion in Two Dimensions

Projectile Motion

Unit 2: Force & Translational Dynamics

Systems & Center of Mass

Describing Systems

Center of Mass

Forces & Free-Body Diagrams

Free Body Diagrams

Forces as Interactions

Net Force

Translational Equilibrium

Newton's Laws

Newton's First Law

Newton's Second Law

Newton's Third Law

Tension

Tension

Tension in Ideal & Non-Ideal Strings

Gravitational Force

Newton's Law of Gravitation

Gravitational Force

Gravitational Field

Acceleration Due to Gravity

Gravitational Field Strength Equation

Weight

Apparent Weight

Inertial vs Gravitational Mass

Kinetic & Static Friction

Kinetic Friction

Kinetic Friction Force Equation

Static Friction

Static Friction Force Formula

Slipping & Sliding

Spring Forces

Hooke's Law

Circular Motion

Uniform Circular Motion

Acceleration in Circular Motion

Circular Motion in a Vertical Loop

Circular Motion Examples

Kepler's Third Law

Unit 3: Work, Energy & Power

Work

Defining Work & Work Done

Calculating Work Done

Translational Kinetic Energy & Potential Energy

Translational Kinetic Energy

Potential Energy

Elastic Potential Energy