Acceleration in Circular Motion (College Board AP® Physics 1: Algebra-Based)

Centripetal acceleration

• Centripetal acceleration is the component of an object’s acceleration directed toward the center of the object’s circular path

  • Centripetal acceleration is always directed toward the center of an object’s circular path along the radius of the circle

• According to Newton's second law the centripetal force that produces the centripetal acceleration is also directed towards the center of the circle

Centripetal force and acceleration

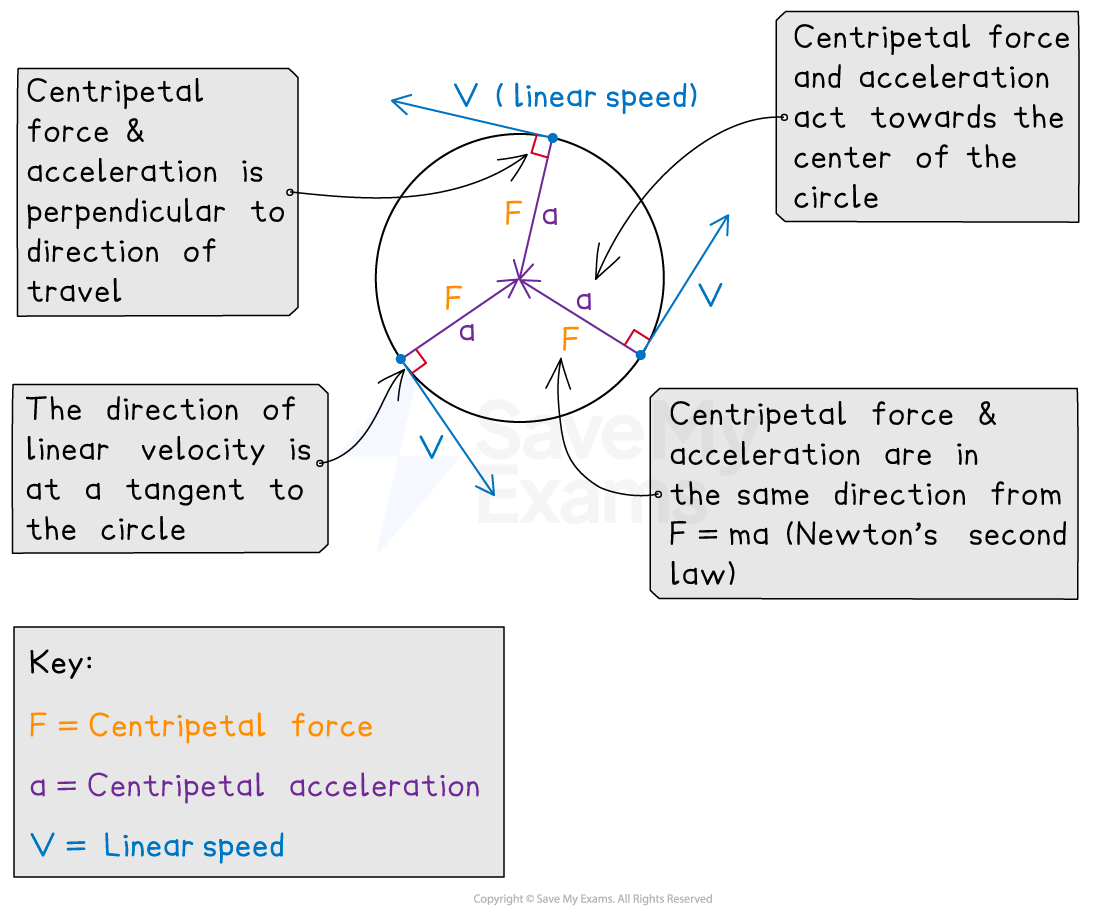
• Centripetal acceleration can result from a single force, more than one force, or components of forces exerted on an object in circular motion

  • The centripetal force can be any type of force, depending on the situation, which keeps an object moving in a circular path

• Examples of single centripetal forces exerted on an object in circular motion include:

  • Tension in a string keeping a ball secured to its end in horizontal circular motion

  • Gravitational force keeping the moon in orbit around the Earth

  • Friction between car tires and the ground keeping a car on the road as it turns a corner

  • Electrostatic force keeping an electron in orbit around a nucleus

Tension as the single centripetal force

• Examples of more than one centripetal force exerted on an object in circular motion include:

  • Tension in a string keeping a ball secured to its end and gravitational force when the ball is swung in a vertical circle

  • Gravitational force and the reaction force of a carriage performing a loop the loop in a vertical circle on a track

• Examples of components of forces exerted on an object in circular motion include:

  • The static friction and weight components of a car on a banked, curved road

  • The tension component of a conical pendulum

Centripetal acceleration equation

• The magnitude of centripetal acceleration for an object moving in a circular path is the ratio of the object’s tangential speed squared to the radius of the circular path

• The magnitude of the centripetal acceleration is given by the equation:

• Where:

  • = magnitude of the centripetal acceleration, measured in

  • = tangential or linear speed, measured in

  • = radius of circular path, measured in

Net acceleration

Tangential acceleration

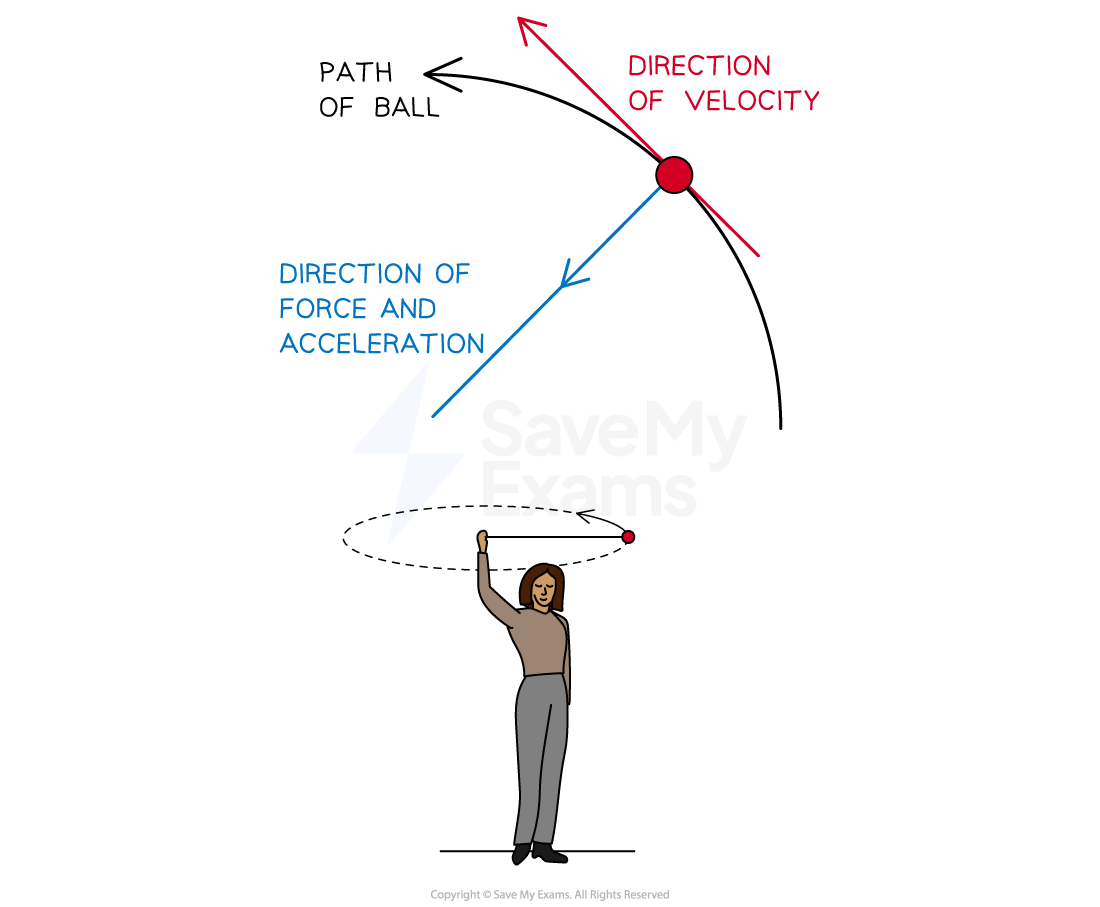
• Tangential acceleration is the rate at which an object’s speed changes and is directed along the tangent to the object’s circular path

  • In a circular path, an object's speed along the tangent to the circular path is also known as its linear speed

  • Linear speed is always at right angles to the direction of centripetal acceleration along the radius of the circle

• Instantaneous speed is the speed at which an object travels in each instant of time

• An object's speed changes between two instants of time, so between two instantaneous speeds

  • The change in speed can be found using the equation

• Where:

  • is the change in speed, measured in

  • is the initial speed, measured in

  • is the final speed, measured in

• Instantaneous speeds and are at different positions on the circular path

Change in instantaneous speed

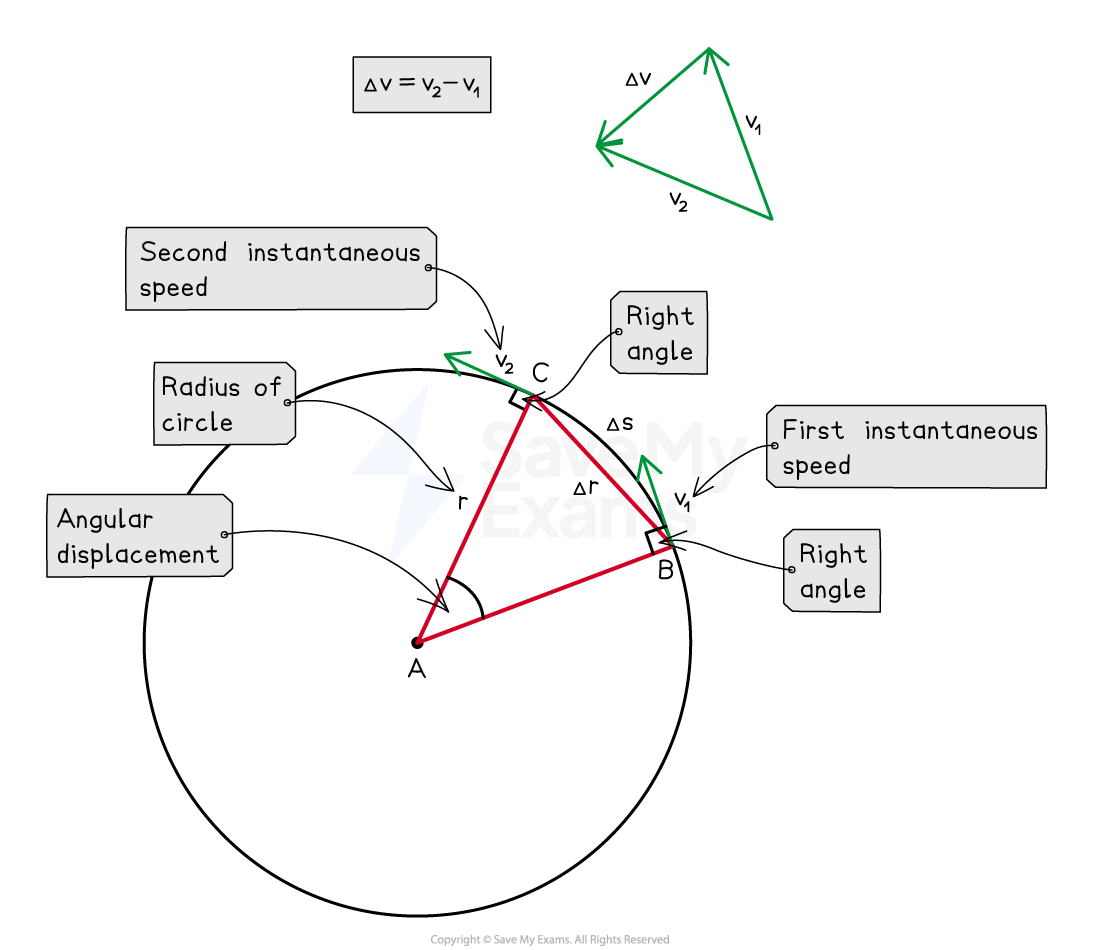
• The rate at which an object's speed changes is given by the change in speed over the time interval,

• So tangential or linear acceleration is given by the equation:

• Where:

  • = tangential acceleration, measured in

  • = change in speed, measured in

  • = time interval, measured in

Net acceleration

• The net acceleration of an object moving in a circle is the vector sum of the centripetal acceleration and tangential acceleration

• The net acceleration of an object moving in a circular path is given by the equation