Study GuidesExam QuestionsPast Papers
AP®PhysicsCollege BoardPhysics 1: Algebra-BasedStudy GuidesUnit 8: FluidsFluid MechanicsTorricelli’s Theorem

Torricelli’s Theorem (College Board AP® Physics 1: Algebra-Based)

Study Guide

Dan Mitchell-Garnett

Written by: Dan Mitchell-Garnett

Reviewed by: Caroline Carroll

Torricelli’s theorem

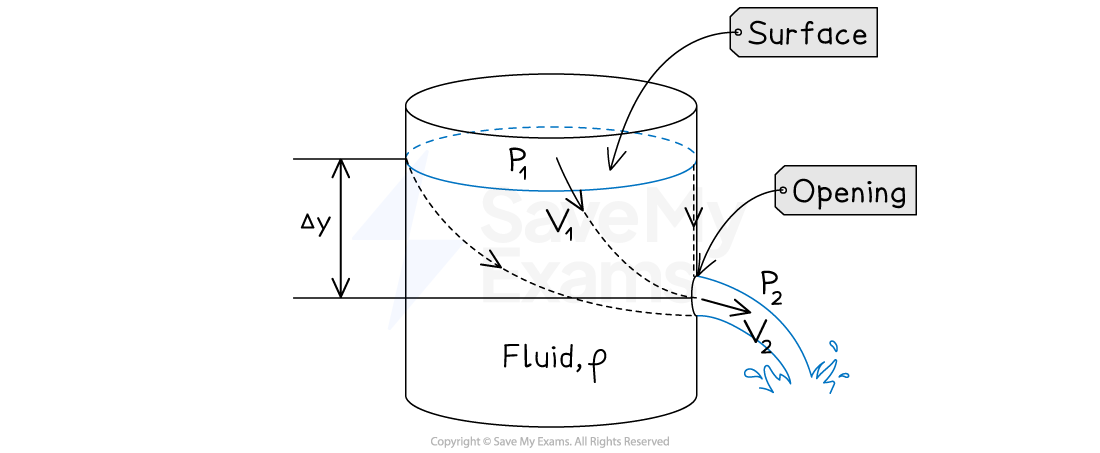
  • Consider a container filled with fluid

  • An opening is cut into the container at a given depth below the fluid's surface

    • This could be in the side of the container or the base, as pressure only depends on depth below the surface, not orientation

  • Torricelli's theorem predicts the speed of fluid exiting the hole

    • It assumes that the surface and opening are both open to the same environment and therefore have matching pressures

Derived equation

  • The speed of fluid leaving an opening in a container is described by the equation:

v space equals space square root of 2 g straight capital delta y end root

  • Where:

    • v = the fluid speed leaving the opening, measured in straight m divided by straight s

    • g = acceleration due to gravity, measured in straight m divided by straight s squared

    • straight capital delta y = distance from the opening to the fluid's surface, measured in straight m

  • Interestingly, this equation shows that the speed depends only on depth

Container with fluid leaving an opening

A fluid of density ρ is in a container. There is an opening in the side of the container at a depth of Δy. Dotted lines represent the flow of fluid from the surface to the opening. At the surface, the fluid is at pressure P_1 and has speed v_1. At the opening, the fluid is at pressure P_2 and has speed v_2.
The speed of fluid exiting through the opening is described by Torricelli's theorem

Derivation

Step 1: Identify the fundamental equations

  • Recall Bernoulli's equation:

P subscript 1 space plus space rho g y subscript 1 space plus space 1 half rho v subscript 1 squared space equals space P subscript 2 space plus space rho g y subscript 2 space plus space 1 half rho v subscript 2 squared

  • Where:

    • P subscript 1 = pressure at point 1, measured in Pa

    • rho = fluid density, measured in kg divided by straight m cubed

    • y subscript 1 = height of point 1 above reference level, measured in straight m

    • v subscript 1 = fluid speed at point 1, measured in straight m divided by straight s

    • P subscript 2 = pressure at point 2, measured in Pa

    • y subscript 2 = height of point 2 above reference level, measured in straight m

    • v subscript 2 = fluid speed at point 2, measured in straight m divided by straight s

  • This compares quantities at the surface (point 1) and the opening (point 2)

Step 2: Apply the specific conditions

  • At the surface, speed is zero, as no fluid is passing through that point, therefore, it can be inferred that:

v subscript 1 space equals space 0 space straight m divided by straight s

  • The reference height can be defined at the same level as the opening, therefore, it can be inferred that:

y subscript 1 space equals space straight capital delta y

y subscript 2 space equals space 0 space straight m

  • Assume that both the fluid's surface and the opening are open to the same atmosphere, therefore, it can be inferred that:

P subscript 1 space equals space P subscript 2 space equals space P subscript a t m end subscript

Step 3: Combine the specific conditions

  • Applying these conditions to Bernoulli's equation gives:

up diagonal strike P subscript a t m end subscript space plus space rho g straight capital delta y space plus space 1 half rho space cross times space 0 squared space equals space up diagonal strike P subscript a t m end subscript space plus space rho g space cross times space 0 space plus space 1 half rho v subscript 2 squared

rho g straight capital delta y space equals space 1 half rho v subscript 2 squared

  • The density terms can be canceled out on each side:

g straight capital delta y space equals space 1 half v subscript 2 squared

  • Rename v subscript 2 as v and rearrange for fluid speed at the opening:

v space equals space square root of 2 g straight capital delta y end root

  • This is Torricelli's theorem

Examiner Tips and Tricks

Understanding the assumptions behind this theorem is as important as the equation itself.

You may be presented with a situation where the pressures are not equal, for example, and just reproducing the above derivation without thought would not score points.

Last updated:

You've read 0 of your 5 free study guides this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Bernoulli’s Equation
    Author
    Reviewer
    Dan Mitchell-Garnett

    Author: Dan Mitchell-Garnett

    Expertise: Physics Content Creator

    Dan graduated with a First-class Masters degree in Physics at Durham University, specialising in cell membrane biophysics. After being awarded an Institute of Physics Teacher Training Scholarship, Dan taught physics in secondary schools in the North of England before moving to Save My Exams. Here, he carries on his passion for writing challenging physics questions and helping young people learn to love physics.

    Caroline Carroll

    Author: Caroline Carroll

    Expertise: Physics Subject Lead

    Caroline graduated from the University of Nottingham with a degree in Chemistry and Molecular Physics. She spent several years working as an Industrial Chemist in the automotive industry before retraining to teach. Caroline has over 12 years of experience teaching GCSE and A-level chemistry and physics. She is passionate about creating high-quality resources to help students achieve their full potential.