Study GuidesExam QuestionsPast Papers
AP®PhysicsCollege BoardPhysics 1: Algebra-BasedStudy GuidesUnit 8: FluidsFluid MechanicsContinuity Equation

Continuity Equation (College Board AP® Physics 1: Algebra-Based)

Study Guide

Dan Mitchell-Garnett

Written by: Dan Mitchell-Garnett

Reviewed by: Caroline Carroll

Continuity equation for fluid flow

  • As previously stated in Fluid Flow Rates, the rate of flow of volume is constant at any point in a pipe

    • This is a consequence of the conservation of mass and the incompressibility of the fluid

  • In equation form, this can be written as:

V over t space equals space constant

  • Where:

    • V = volume passing a point, measured in straight m cubed

    • t = time taken for that volume to pass the point, measured in straight s

  • Recall the equation for rate of flow of volume at a given point:

V over t space equals space A v

  • Where:

    • A = cross-sectional area of the flow at that point, measured in straight m squared

    • v = speed of the flow at that point, measured in straight m divided by straight s

  • If the left side is constant, the right side is also constant:

A v space equals space constant

  • This can be used to compare two points in the same pipe

Comparing flow at two points in a pipe

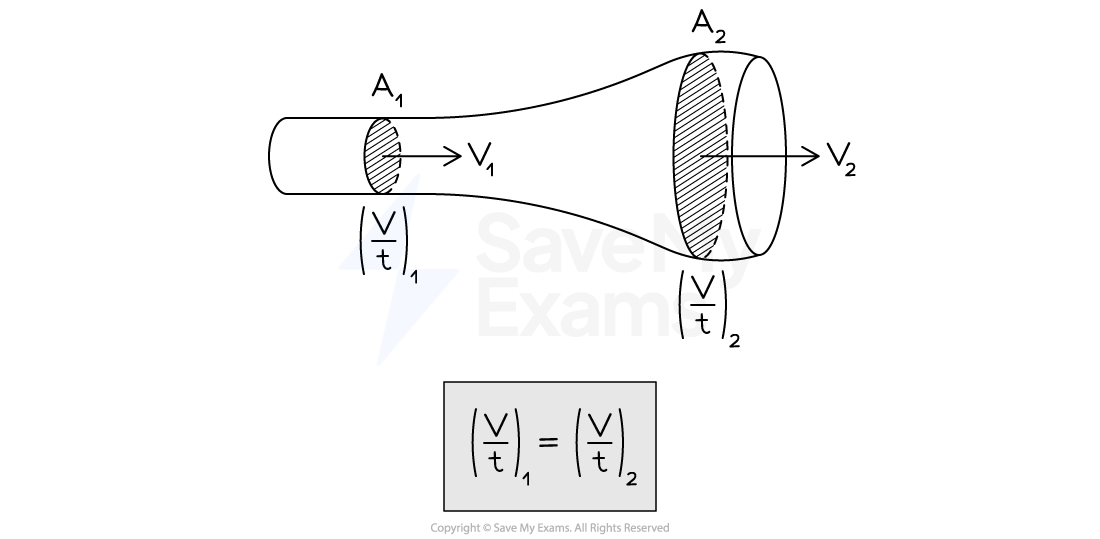
A pipe is narrow on the left and wide on the right. Point 1 is narrow and has an area labelled A_1 and flow speed v_1. Flow rate is labelled as (V/t)_1. Point 2 is wide and has an area labelled A_2 and flow speed v_2. Flow rate is labelled as (V/t)_2. The equation (V/t)_1 = (V/t)_2 is below the diagram.
The flow rate at points 1 and 2 are equal, meaning the product of area and speed is constant throughout the pipe.

  • When comparing the flow rate at two points in a pipe, labelled 1 and 2, this becomes:

A subscript 1 v subscript 1 space equals space A subscript 2 v subscript 2

  • Where:

    • A subscript 1 = cross-sectional area of the flow at point 1, measured in straight m squared

    • v subscript 1 = speed of the flow at point 1, measured in straight m divided by straight s

    • A subscript 2 = cross-sectional area of the flow at point 2, measured in straight m squared

    • v subscript 2 = speed of the flow at point 2, measured in straight m divided by straight s

  • This is known as the continuity equation

Examiner Tips and Tricks

Remember that fluid speed and area are inversely proportional, but fluid speed is inversely proportional to the square of radius.

Last updated:

You've read 0 of your 5 free study guides this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Fluid Flow RatesNext:Bernoulli’s Equation
    Author
    Reviewer
    Dan Mitchell-Garnett

    Author: Dan Mitchell-Garnett

    Expertise: Physics Content Creator

    Dan graduated with a First-class Masters degree in Physics at Durham University, specialising in cell membrane biophysics. After being awarded an Institute of Physics Teacher Training Scholarship, Dan taught physics in secondary schools in the North of England before moving to Save My Exams. Here, he carries on his passion for writing challenging physics questions and helping young people learn to love physics.

    Caroline Carroll

    Author: Caroline Carroll

    Expertise: Physics Subject Lead

    Caroline graduated from the University of Nottingham with a degree in Chemistry and Molecular Physics. She spent several years working as an Industrial Chemist in the automotive industry before retraining to teach. Caroline has over 12 years of experience teaching GCSE and A-level chemistry and physics. She is passionate about creating high-quality resources to help students achieve their full potential.