AP®PhysicsCollege BoardPhysics 1: Algebra-BasedStudy GuidesUnit 8: FluidsFluid MechanicsBuoyant Force

Buoyant Force (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself
Dan Mitchell-Garnett

Expertise

Physics Content Creator

Buoyant force

  • A buoyant force is a net upward force on an object in a fluid, arising from a pressure difference at its top and bottom

  • The pressure exerted on the surface of a submerged object is a result of the forces exerted on it by the particles making up the fluid

  • Recall that gauge pressure depends on depth only

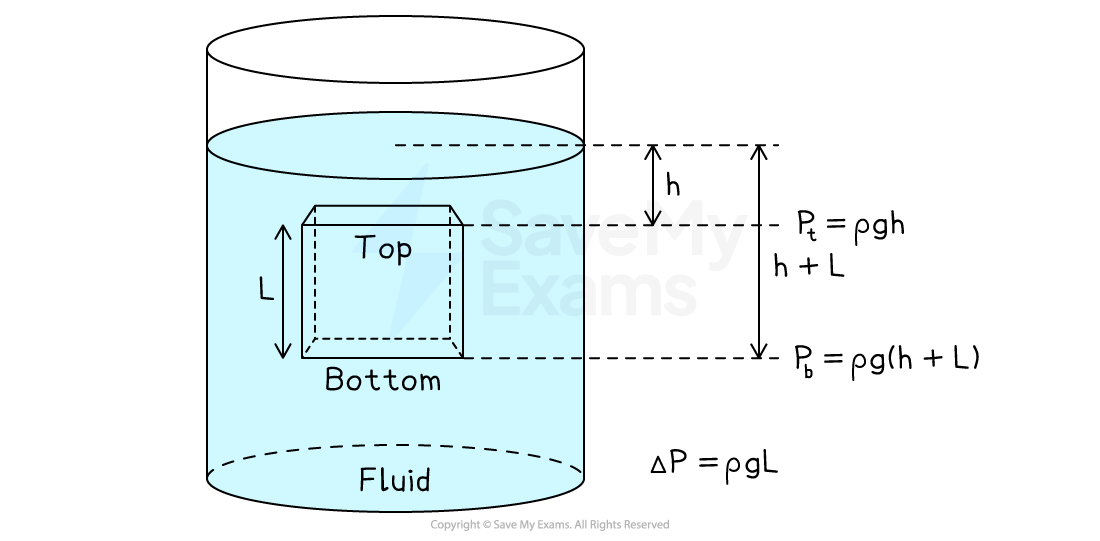
  • Consider a submerged three-dimensional object, such as a cube:

    • It has multiple surfaces

    • Some surfaces are at different depths

    • These experience different pressures forces from the particles in the fluid

  • The cube's bottom surface experiences a greater pressure than the top surface and, therefore, a greater perpendicular force

    • There is a net upward force from the fluid, called the buoyant force

  • This buoyant force is a direct result of all the forces exerted on the object by the particles that make up the fluid

Pressure difference on a 3D object

The top face of the cube is at a depth h in a fluid and experiences a pressure of rho x g x h. The cube has side length L and the bottom face experiences a pressure of rho x g x (h + L). The pressure difference is rho x g x L.
The top and bottom faces of a submerged cube experience different gauge pressures.

Buoyant force equation

Archimedes' Principle

  • Archimedes' principle describes the size of this force:

The magnitude of buoyant force is equal to the weight of the fluid displaced by the object

  • One consequence of this is that buoyant force is independent of the object's mass

  • Two objects of identical shape but different masses will experience the same buoyancy

Buoyant force equation

  • In equation form, this buoyant force can be calculated as:

F subscript b space equals space rho V g

  • Where:

    • F subscript b = buoyant force, measured in straight N

    • rho = density of the fluid, measured in kg divided by straight m cubed

    • V = volume of fluid displaced, measured in straight m cubed

    • g = acceleration due to gravity, measured in straight m divided by straight s squared

Submerged volume

  • The volume in this equation refers to the volume of fluid displaced

    • This is equal to the volume of the object that is submerged in the fluid

  • In the above equation, the V term can cause confusion:

    • If the object is fully submerged, V is simply the object's volume

    • If the object is partially submerged, V is the volume of the object below the surface

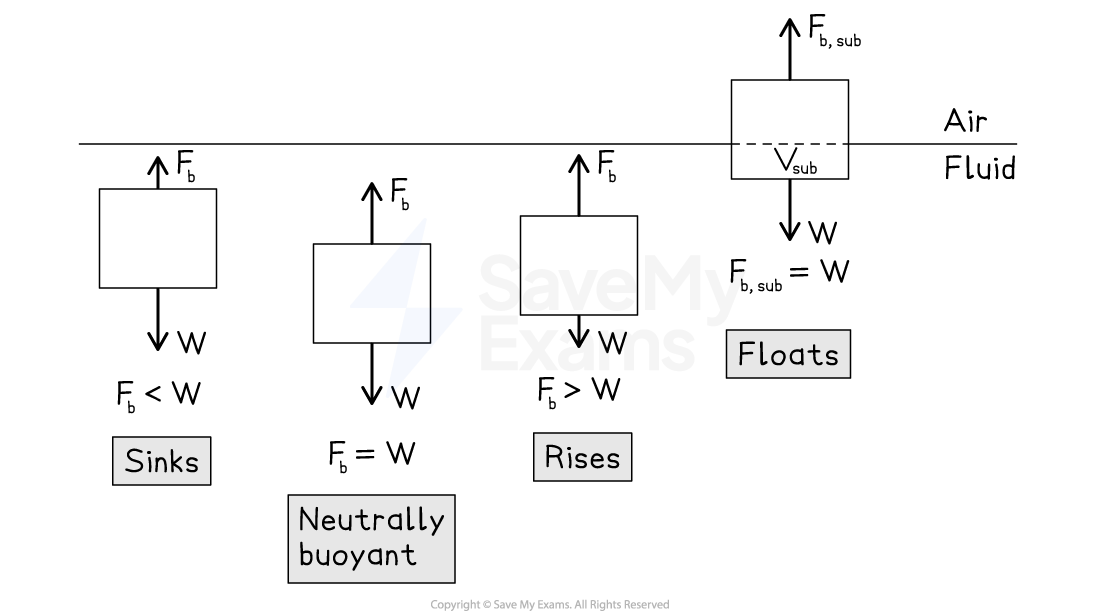
Floating

  • An object experiences maximum buoyancy when it is fully submerged

    • Here, it displaces the greatest amount of fluid

  • If the object's weight is greater than this buoyant force, the object will sink

    • There is a net force downwards

  • If the object's weight matches this buoyant force, the object will remain submerged but not sink

    • This is sometimes called neutral buoyancy

  • If the object's weight is less than the maximum buoyant force, the object will float

    • The amount of the object which is submerged is such that the buoyant force is equal to the object's weight

Conditions for floating and sinking

4 objects in a fluid are shown. Sinking object: weight is greater than buoyant force Neutrally buoyant object: weight equals buoyant force Rising object: object is submerged, but weight is less than buoyant force Floating object: object protrudes above the surface of the fluid but volume V_sub is below the surface. The buoyant force from this submerged volume, F_b,sub, is equal to the whole object's weight.
The net vertical force on an object determines whether it sinks or floats. When buoyant force is greater than weight, the object will rise above the fluid until the buoyant force from its submerged volume equals its weight.

Worked Example

A wooden cube hangs from a Newton meter, which reads a force of 16.0 N. When the wooden cube is submerged in oil to exactly half its height, the reading on the Newton meter is 12.0 N. When the reading is taken, the wooden cube is at rest and does not touch the sides of the container.

The density of the oil is 700 kg/m3.

What is the width of the wooden cube?

A      0.6 cm

B      8.4 cm

C      11.0 cm

D      15.0 cm

The correct answer is C

Answer:

Step 1: Analyze the scenario

  • When the cube is not submerged, the Newton meter reading is 16.0 N - this is the cube's weight

  • When the cube is submerged halfway, the measured weight is reduced

  • The buoyant force from the oil causes this perceived reduction in weight

  • Only half of the cube's volume is displacing fluid

Step 2: Determine the size of the buoyant force

  • When submerged, the Newton meter measures a net force of 12.0 N

  • The net force is equal to the difference between the weight (where W = 16.0N) and the buoyant force

F subscript n e t end subscript space equals space W space minus space F subscript b

12 space equals space 16 space minus space F subscript b

F subscript b space equals space 4.0 space straight N

  • The buoyant force on the cube is 4.0 N

Step 3: Determine the volume of fluid displaced

  • The magnitude of the buoyant force is:

F subscript b space equals space rho V g

  • Where V is the volume of fluid displaced and space rho is the density of the fluid, which is 700 kg/m3 for oil

4.0 space equals space 700 space cross times space V space cross times space 9.8

  • Rearrange for the volume of fluid displaced:

V space equals space fraction numerator 4.0 over denominator 700 space cross times space 9.8 end fraction space equals space 5.831 space cross times space 10 to the power of negative 4 end exponent space straight m cubed

  • Option A can be discounted, as this is the volume of fluid displaced, not the width of the cube

Step 4: Determine the width of the cube

  • The volume of fluid displaced is equal to half the volume of the cube

V space equals space 1 half V subscript c u b e end subscript

  • The volume of a cube is given by the equation

V subscript c u b e end subscript space equals space L cubed

  • Where L is the length of all sides of the cube, including width

  • Substituting this and rearranging for L gives the width of the cube

V space equals space 1 half L cubed

L space equals space cube root of 2 V end root space equals space cube root of 2 space cross times space open parentheses 5.831 space cross times space 10 to the power of negative 4 end exponent close parentheses end root

width space equals space L space equals space 0.11 space straight m space equals space 11 space cm

  • This most closely matches option C

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfNext topic

    Did this page help you?

    Dan Mitchell-Garnett

    Author: Dan Mitchell-Garnett

    Expertise: Physics Content Creator

    Dan graduated with a First-class Masters degree in Physics at Durham University, specialising in cell membrane biophysics. After being awarded an Institute of Physics Teacher Training Scholarship, Dan taught physics in secondary schools in the North of England before moving to Save My Exams. Here, he carries on his passion for writing challenging physics questions and helping young people learn to love physics.