Torque & Work (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself

Author

Katie M

Expertise

Physics

Work done by torque

When a torque is exerted over an angular displacement, energy is transferred into or out of an object or rigid system
- Some examples of this include rotating cranes and fairground rides
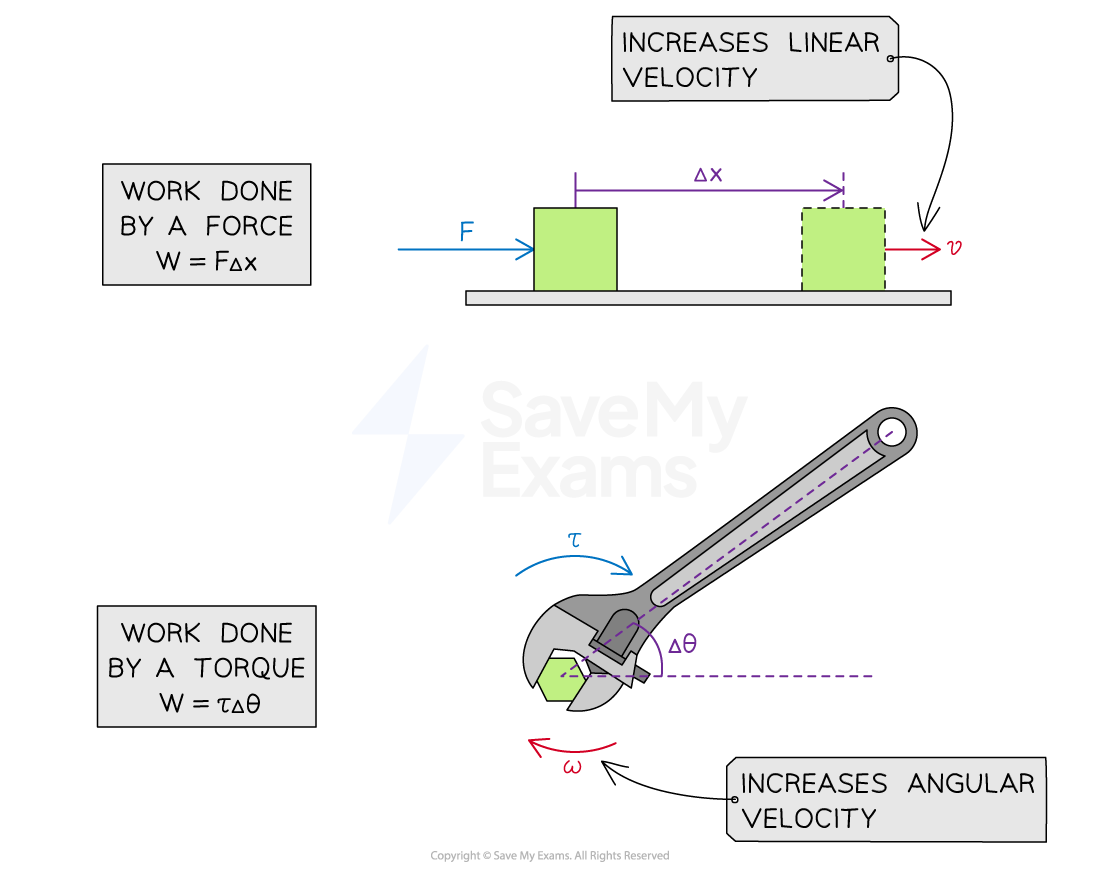
The work done on a rigid system by a torque is given by:

$W = τ ∆ θ$

Where:
- $W$ = work done, in $J$
- $τ$ = torque, in $N \cdot m$
- $∆ θ$ = angular displacement, in $rad$
Equivalent amounts of work can be done on a rigid system by
- exerting a smaller torque over a greater angle of rotation
- exerting a larger torque over a smaller angle of rotation
This is analogous to systems with linear acceleration, where work done is the product of the force and the linear displacement

Comparing work done on translational and rotational systems

Comparing work done by a force and by a torque.
Top: work is done by a force F moving an object over a displacement Δx increasing linear velocity v.
Bottom: work is done by a torque τ rotating a wrench over an angular displacement Δθ, increasing angular velocity ω. — **Work done by a torque is analogous to the work done by a force, but instead leads to an increase in angular velocity**

Worked Example

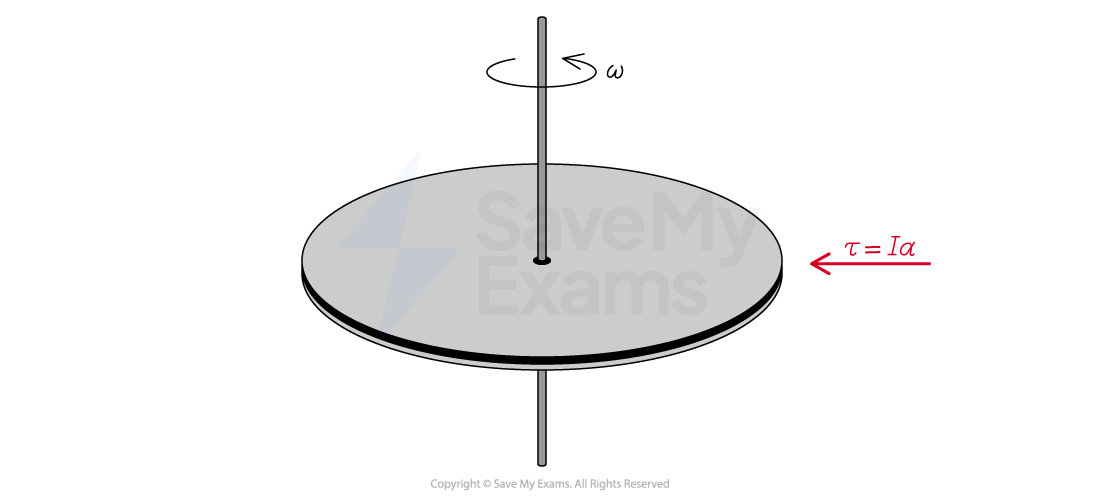
A horizontally mounted wheel with rotational inertia $I$ spins about a frictionless axle. At time t = 0, the angular speed of the wheel is $ω$ . A constant torque $τ$ is applied to the wheel which causes it to come to rest in time $t$ .

Derive an expression for the average power required to dissipate the wheel's energy in terms of $I$ , $ω$ and $t$ .

Answer:

Step 1: Analyze the scenario

Initially, the wheel spins with an initial angular speed of $ω_{0} = ω$
After time $∆ t = t$ , the wheel has a final angular speed of $ω = 0$
The torque $τ$ applied to the wheel is constant, therefore the angular acceleration $α$ is also constant
Hence, we can use the rotational form of Newton's second law as well as the equations of constant angular acceleration in our derivation

A rotating wheel with angular velocity ω is slowed by a torque τ = Iα, shown by an arrow pointing to the wheel's rim and a black curved arrow showing rotation direction.

Step 2: Write an expression for the average power supplied to the wheel

The work done on the wheel is:

$W = τ ∆ θ$

The torque applied to the wheel is:

$τ = I α$

Therefore, the average power supplied to the wheel is:

$P_{a v g} = \frac{W}{∆ t} = \frac{τ ∆ θ}{∆ t} = \frac{I α ∆ θ}{∆ t}$

Step 3: Write an expression for the angular acceleration of the wheel

The rotational kinematic equation relating $ω$ , $ω_{0}$ , $α$ and $t$ is:

$ω = ω_{0} + α t$

Where $ω_{0} = ω$ and $ω = 0$ :

$0 = ω + α t \Rightarrow α = - \frac{ω}{t}$

Step 4: Write an expression for the angular displacement of the wheel

The rotational kinematic equation relating $ω$ , $ω_{0}$ , $θ$ and $t$ is:

$∆ θ = \frac{1}{2} (ω_{0} + ω) t$

Where $ω_{0} = ω$ and $ω = 0$ :

$∆ θ = \frac{1}{2} (ω + 0) t \Rightarrow ∆ θ = \frac{1}{2} ω t$

Step 5: Combine the equations and simplify

Substituting these equations into the expression for power:

$P_{a v g} = \frac{I α ∆ θ}{∆ t}$

$P_{a v g} = \frac{I (- \frac{ω}{t}) (\frac{1}{2} ω t)}{t}$

$P_{a v g} = - \frac{I ω^{2}}{2 t}$

Torque-angular position graph

A changing torque can be plotted as a function of angular displacement
The work done on a rigid system is equal to the product of torque and angular displacement
Therefore, the area under the torque-angular position graph is equal to
- work done
- change in kinetic energy

$area = τ ∆ θ = W = ∆ K$

Determining work done from a torque-angular displacement graph

The relationship between torque (Nm) and angular displacement (radians), illustrating that the area under the curve represents the work done. — **The work done is the area under the torque-angular displacement graph**

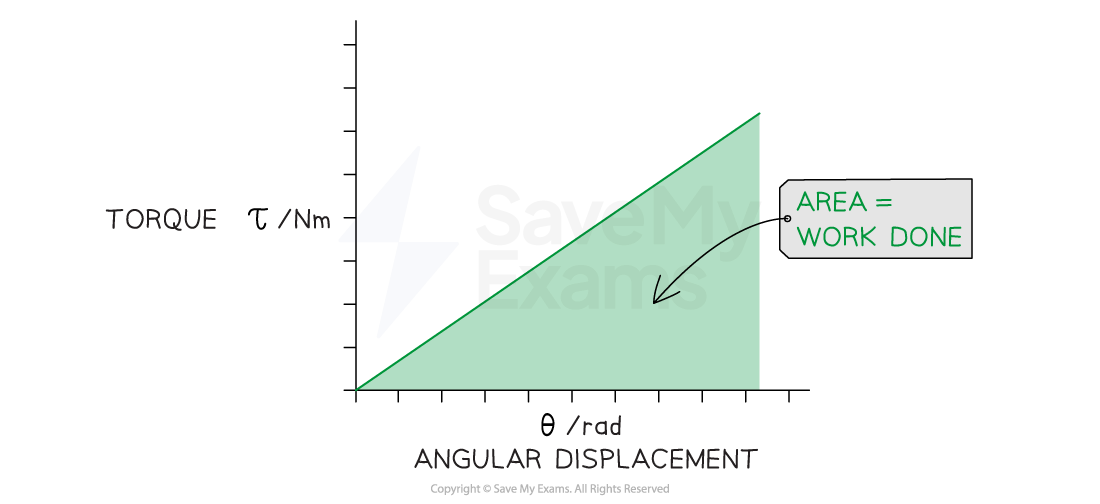
The graph may show positive or negative values of torque
- Positive areas represent positive work i.e. energy added to the system
- Negative areas represent negative work i.e. energy removed from the system
This is analogous to linear work done being equal to the area under a force-displacement graph

Worked Example

A cylinder of mass 5.0 kg and radius 0.20 m is mounted on an axle parallel to its axis and through its center of mass. The rotational inertia of the cylinder about this axis is $\frac{1}{2} M R^{2}$ . The cylinder is initially at rest before a force is applied to a point on its edge which causes it to rotate. The graph shows the net torque exerted on the cylinder as a function of angular position.

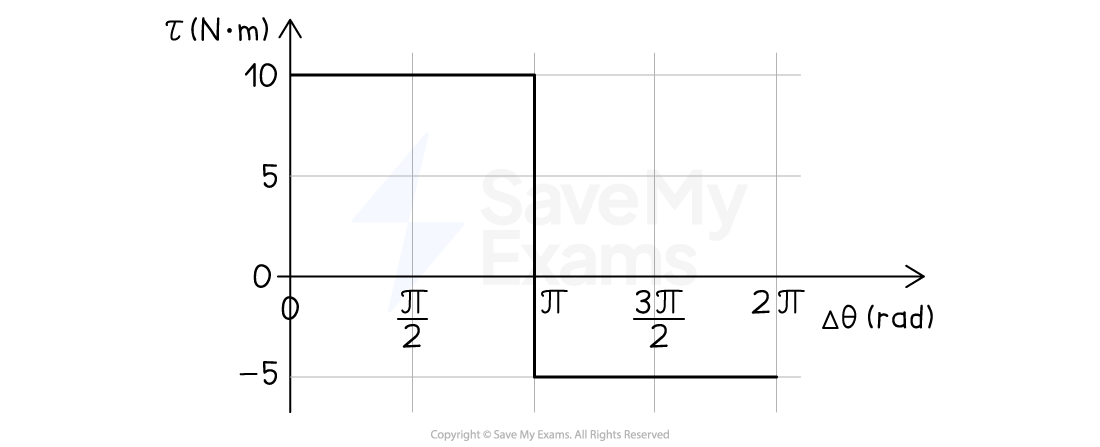
Plot of torque (τ) in N·m versus angular position (Δθ) in radians. The graph features stepped changes at π/2, π, and 3π/2 with values of 10, 0, and -5 N·m.

Determine the angular velocity of the cylinder after it completes one full revolution.

Answer:

Step 1: Analyze the scenario

One full revolution is equivalent to 2π rad
A constant positive torque of 10 N·m is applied until the cylinder rotates through π rad
At $θ$ = π rad, the direction of the applied torque changes
A constant negative torque of −5 N·m is then applied as the cylinder rotates through another π rad
Overall, the work done on the cylinder:
- is positive from $θ$ = 0 to $θ$ = π, so the angular velocity will increase
- is negative from $θ$ = π to $θ$ = 2π, so the angular velocity will decrease

Step 2: Determine the work done over the 2π rotation

The area under a torque-angular position graph is equal to the work done, or the change in kinetic energy

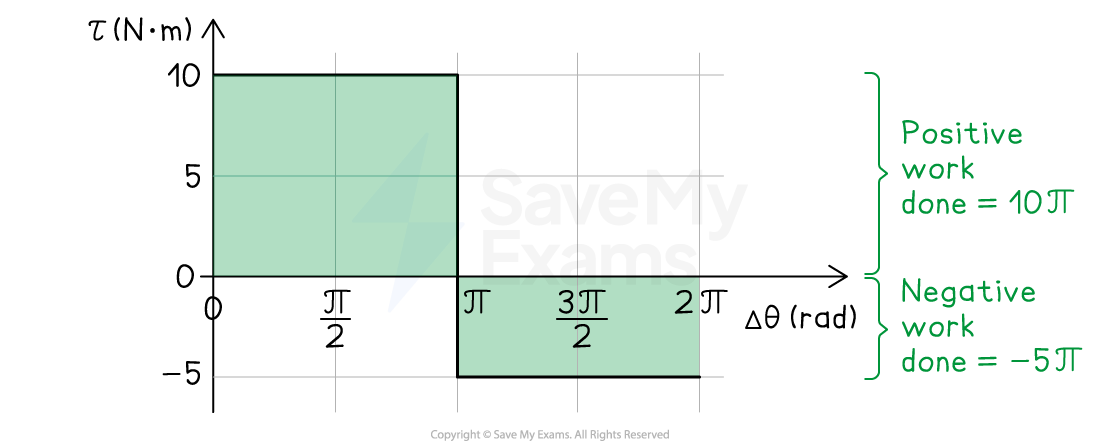
Graph showing torque (τ in N·m) vs angular displacement (Δθ in radians). Green areas represent positive work (10π) from 0 to π rad and negative work (−5π) from π to 2π radians.

Area under the positive section = $10 \times π = 10 π J$
Area under the negative section = $- 5 \times π = - 5 π J$
Therefore, the work done, or net change in kinetic energy is:

$W = ∆ K = 10 - 5 = 5 π J$

Step 3: Determine the final angular velocity of the cylinder

The change in kinetic energy is equal to

$∆ K = \frac{1}{2} I ω^{2} = \frac{1}{2} (\frac{1}{2} M R^{2}) ω^{2} = \frac{1}{4} M R^{2} ω^{2}$

Where $M$ = 5.0 kg and $R$ = 0.20 m (and $ω_{0}$ = 0)
Therefore, after a full revolution $(∆ θ = 2 π)$ , the cylinder's angular velocity is:

$ω = \sqrt{\frac{4 ∆ K}{M R^{2}}}$

$ω = \sqrt{\frac{4 \times 5 π}{5.0 \times 0 . 20^{2}}}$

$ω = 17.8 rad / s$

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Next topic

Did this page help you?

Torque & Work (College Board AP® Physics 1: Algebra-Based)

Study Guide

Work done by torque

Comparing work done on translational and rotational systems

Worked Example

Torque-angular position graph

Determining work done from a torque-angular displacement graph

Worked Example

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Katie M