AP®PhysicsCollege BoardPhysics 1: Algebra-BasedStudy GuidesUnit 6: Energy & Momentum of Rotating SystemsRotational Kinetic Energy, Torque & WorkRotational Kinetic Energy

Rotational Kinetic Energy (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself
Katie M

Author

Katie M

Expertise

Physics

Rotational kinetic energy equation

  • Rotational kinetic energy is the energy associated with rotational motion

  • It is given by the equation:

K space equals space 1 half I omega squared

  • Where:

    • K = rotational kinetic energy, in straight J

    • I = rotational inertia, in kg times straight m squared

    • omega = angular velocity, in rad divided by straight s

  • Rotational kinetic energy, like other forms of energy, is a scalar quantity

Comparing translational and rotational energy

  • Rotational kinetic energy is not a new type of energy, it is a type of kinetic energy, analogous to translational kinetic energy

  • On a rotating body, the distribution of mass is described by its rotational inertia

  • The rotational inertia of an object about a fixed axis is given by:

I space equals space m r squared

  • Where:

    • m = mass of the object, in kg

    • r = distance to the axis of rotation, in straight m

  • At different points on a rotating body, the translational (linear) velocity varies, but the angular velocity is the same at all points

  • For a single point rotating about a fixed axis, the angular speed is given by:

omega space equals space v over r

  • Where:

    • v = linear velocity, in straight m divided by straight s

  • Substituting these into the equation for rotational kinetic energy:

K space equals space 1 half I omega squared space equals space 1 half open parentheses m r squared close parentheses open parentheses v over r close parentheses squared space equals space 1 half m v squared

  • This shows that the rotational kinetic energy of an object is equivalent to its translational kinetic energy

Total kinetic energy of rigid systems

  • Rigid circular objects, such as wheels, move with both translational and rotational motion

    • For example, the wheels of a car or a bicycle rotate causing it to move forward

  • Newton's laws for rotational motion remain valid as long as:

    • the axis of rotation passes through the object's center of mass

    • the direction of rotation does not change

  • The total kinetic energy K subscript t o t a l end subscript of a rigid system is a combination of:

    • the rotational kinetic energy K subscript r due to its rotation about its center of mass

    • the translational kinetic energy K subscript t due to the linear motion of its center of mass

  • This can be written as:

K subscript t o t a l end subscript space equals space K subscript r space plus space K subscript t

K subscript t o t a l end subscript space equals space 1 half I omega squared space plus space 1 half m v squared

  • A rigid system can have rotational kinetic energy even if its center of mass is at rest

    • This is because individual points within the system can have linear speed and, therefore, kinetic energy

    • As a result, the whole system rotates about the stationary center of mass

  • Examples of this include:

    • flywheels

    • turntables

    • merry-go-rounds

Worked Example

A flywheel of mass M and radius R rotates at a constant angular velocity omega about an axis through its center. The rotational kinetic energy of the flywheel is K.

The rotational inertia of the flywheel is 1 half M R squared.

A second flywheel of mass 1 half M and radius 1 half R is placed on top of the first flywheel. The new angular velocity of the combined flywheels is 2 over 3 omega.

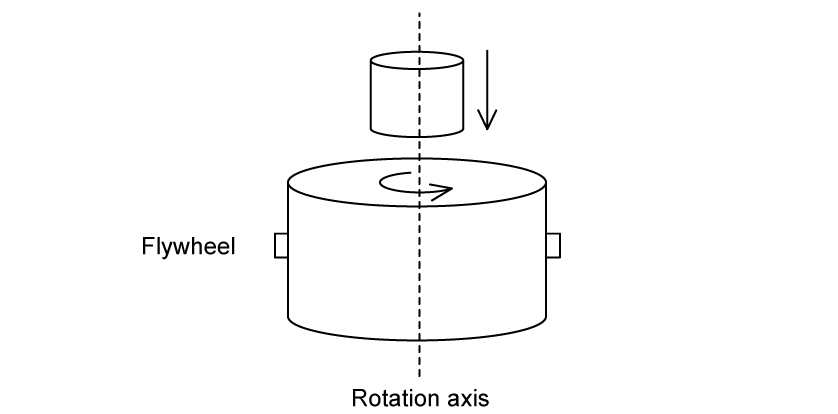
A smaller flywheel is dropped onto a larger flywheel. The flywheel rotates around a central vertical axis in an anticlockwise direction.

What is the new rotational kinetic energy of the combined flywheels?

A      K over 2

B      K over 4

C      K over 8

D      K over 24

The correct answer is A

Answer:

Step 1: Determine the rotational kinetic energy of the first flywheel

K space equals space 1 half I omega squared space equals space 1 half open parentheses 1 half M R squared close parentheses omega squared

K space equals space 1 fourth M R squared omega squared

Step 2: Determine the total rotational inertia of the combined flywheels

I subscript n e w end subscript space equals space I subscript 1 space plus space I subscript 2

I subscript n e w end subscript space equals space 1 half M R squared space plus space 1 half open parentheses 1 half M close parentheses open parentheses 1 half R close parentheses squared

I subscript n e w end subscript space equals space 9 over 16 M R squared

Step 3: Determine the rotational kinetic energy of the combined flywheels

K subscript n e w end subscript space equals space 1 half I subscript n e w end subscript omega subscript n e w end subscript squared space equals space 1 half open parentheses 9 over 16 M R squared close parentheses open parentheses 2 over 3 omega close parentheses squared

K subscript n e w end subscript space equals space 1 half open parentheses 1 fourth M R squared omega close parentheses space equals space 1 half K

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfNext topic

    Did this page help you?

    Katie M

    Author: Katie M

    Expertise: Physics

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.