Rolling (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself

Written by: Katie M

Reviewed by: Caroline Carroll

Total kinetic energy

The total kinetic energy of a system is the sum of translational and rotational kinetic energies:

total kinetic energy = translational kinetic energy + rotational kinetic energy

$K_{t o t a l} = K_{t r a n s} + K_{r o t}$

$K_{t o t a l} = \frac{1}{2} m v^{2} + \frac{1}{2} I ω^{2}$

Where:
- $m$ = mass of the object, in $kg$
- $v$ = linear velocity, in $m / s$
- $I$ = rotational inertia, in $kg \cdot m^{2}$
- $ω$ = angular velocity, in $rad / s$

When considering the mechanical energy of a system, the kinetic energy can be broken down into its translational and rotational components

$E = ∆ K + ∆ U$

$E = ∆ (K_{t r a n s} + K_{r o t}) + ∆ U$

Two special cases involving rotational kinetic energy are
- rolling motion without slipping
- rolling motion while slipping

Rolling without slipping

Rolling motion is a combination of rotating and sliding (translational) motion
When a circular rigid body (e.g. a ball, wheel, or cylinder) of radius $r$ rolls without slipping:
- the translational motion of the system's center of mass is directly related to its rotational motion
- the point of contact between the rotating body and the surface is at rest

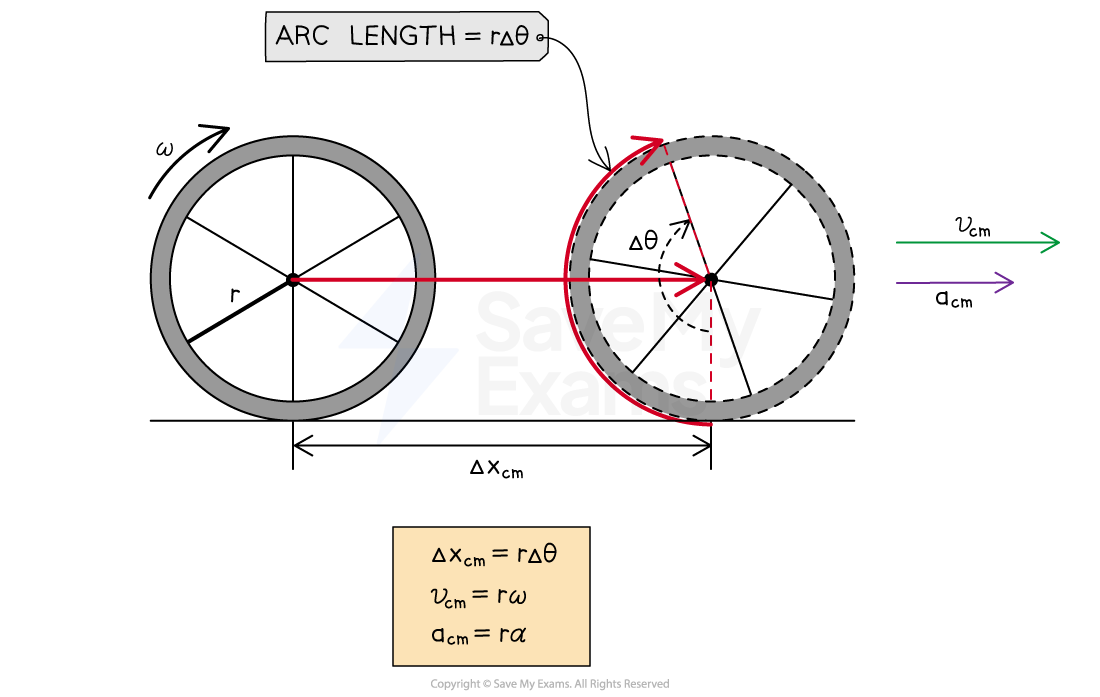
The distance traveled by the system's center of mass is:

$∆ x_{c m} = r ∆ θ$

Where:
- $∆ x_{c m}$ = translational distance moved by the object's center of mass, in $m$
- $∆ θ$ = angular displacement of the rolling object, in $rad$
The linear velocity of the system's center of mass is:

$v_{c m} = r ω$

Where:
- $v_{c m}$ = translational velocity of the object's center of mass, in $m / s$
- $ω$ = angular speed of the rolling object, in $rad / s$
The linear acceleration of the system's center of mass is:

$a_{c m} = r α$

Where:
- $a_{c m}$ = translational acceleration of the object's center of mass, in $m / s^{2}$
- $α$ = angular acceleration of the rolling object, in $rad / s^{2}$
These equations appear to be identical to the equations for fixed-axis rotation, but there are some key differences
- For fixed axis rotation: $s$ , $v$ , and $a$ refer to the tangential quantities at a point on the object
- For a rolling object: $∆ x_{c m}$ , $v_{c m}$ , and $a_{c m}$ refer to the translational quantities of the object's center of mass

Translational and rotational components of a rotating wheel

A rotating wheel with radius r and angular velocity ω. The distance traveled by the wheel is equal to the arc length that has been in contact with the ground. The relationships between velocity, acceleration and their equivalent angular variables are also shown. — The linear velocity and acceleration of the center of mass of a rotating wheel are proportional to its angular counterparts. As the wheel rolls on a surface, the arc length that has been in contact with the ground is equal to the distance traveled by the center of mass

The role of friction in rolling without slipping

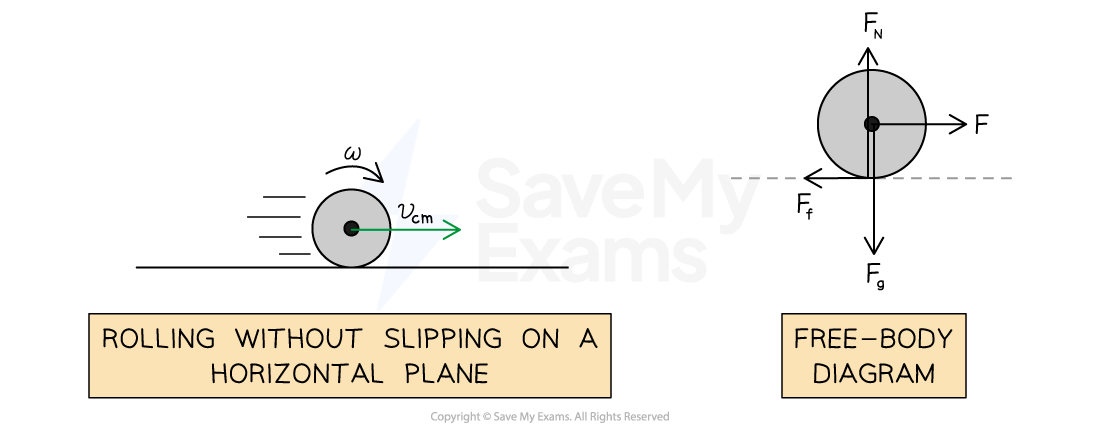
When an object rolls without slipping, static friction causes the rotation about the center of mass
This happens when there is no relative motion between the surface and the point of contact
The direction of the frictional force always acts to oppose the potential slipping motion

Static friction causing rolling on a horizontal plane

Two diagrams: a ball rolling on a flat surface with speed lines and a free-body diagram showing forces (gravity, normal, friction, and applied force). — **When a circular rigid body is pulled across a horizontal surface by a force F, the force of static friction is large enough to keep it from slipping.**

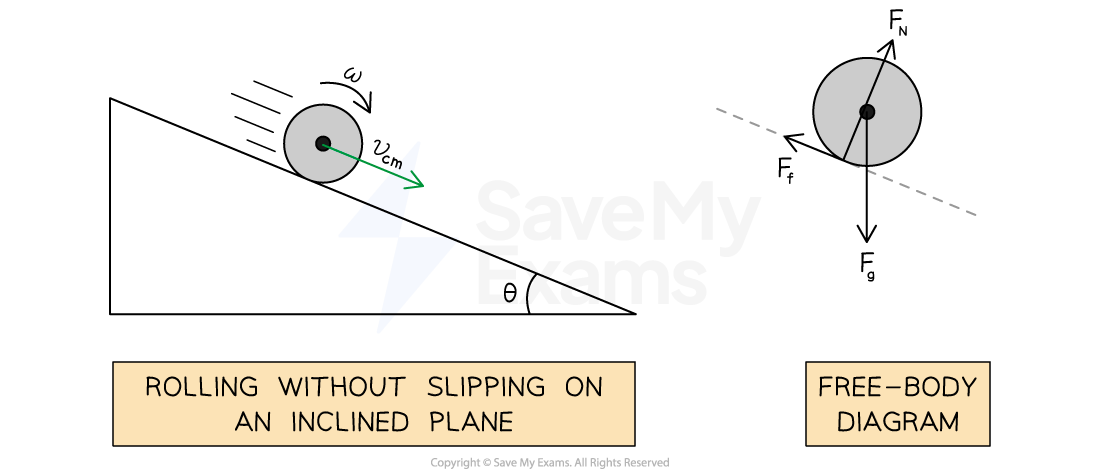
Static friction causing rolling on an inclined plane

A ball rolling down an inclined plane with angle θ without slipping. The free-body diagram shows the normal force, the static friction force, and the weight. — **When a circular rigid body rolls down an inclined plane, the force of static friction is large enough to make it roll instead of slip**

In the case of rolling motion without slipping:
- no kinetic friction is present
- only static friction is present

Since no work is done by static friction, no energy is dissipated when a system rolls without slipping

Rolling on a horizontal surface without slipping

When a disk rotates on a horizontal surface:
- all points on the disk have a constant angular speed
- each point on the disc has a different linear velocity depending on its distance from the center $(v \propto r)$
- the linear speed is the same at all points on the circumference

When a disk slips or slides on a horizontal surface:
- there is not enough static friction present to allow the object to roll
- all points on the disk have the same linear velocity
- the angular velocity is zero
So, when a disk rolls without slipping:
- there is enough static friction present to initiate rotational motion allowing the object to roll
- the point in contact with the surface has a velocity of $v = 0$
- the center of mass has a velocity of $v_{c m} = ω r$
- the top point has a velocity of $v = 2 ω r$ , or $2 v$

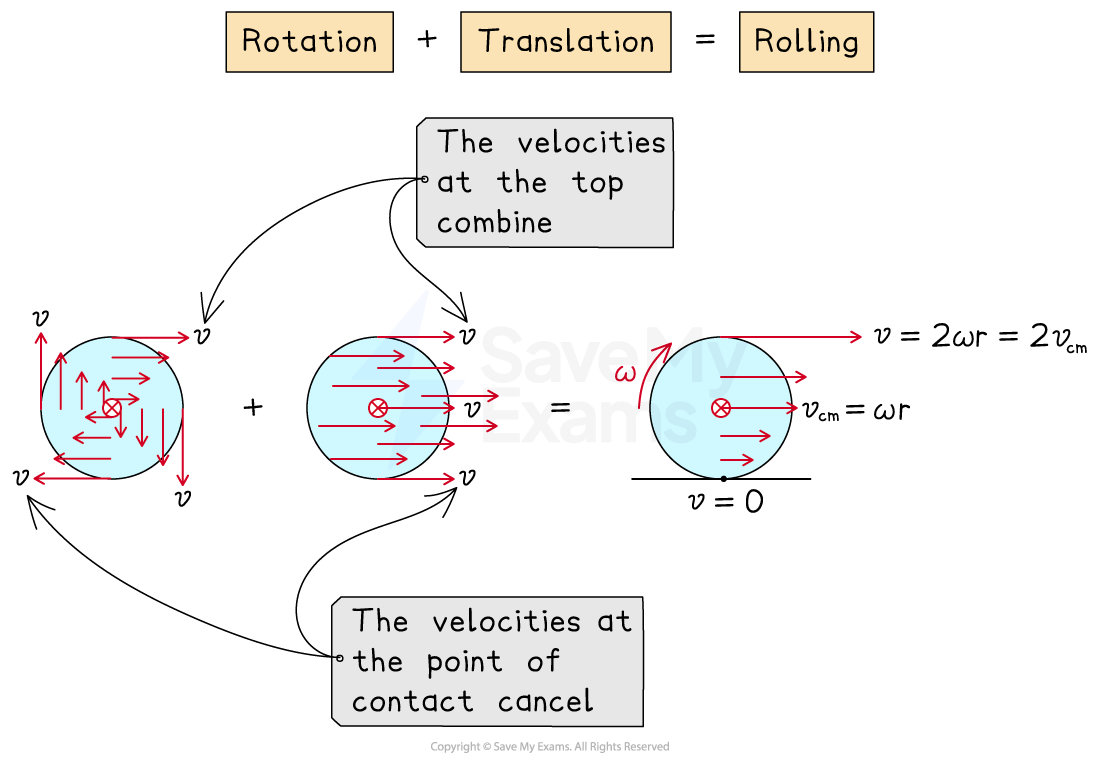
A rolling disc with rotational plus translational motion. The velocity vectors cancel and add together to demonstrate the net effect on a rolling object. At the top: v = 2ωr. At the center of mass: v = ωr. At the bottom: v = 0. — **Rolling motion is a combination of rotational and translational motion. The resultant velocity at the bottom is zero and the resultant velocity at the top is 2v**

Rolling on an inclined plane without slipping

Another common scenario is a circular rigid body rolling on an inclined plane without slipping
Since the object rolls without slipping, no work is done by frictional forces
Therefore, the total mechanical energy of the system is conserved
- At the top of the slope, the object has gravitational potential energy only (assuming it is initially at rest)
- As the object rolls down the slope, the gravitational potential energy is transferred to kinetic energy
- At the bottom of the slope, the object has both translational and rotational kinetic energy
The linear or angular velocity can then be determined by:
- applying energy conservation laws
- using the equation for the rotational inertia of the object
- using the relationship between linear and angular velocity $v_{c m} = ω r$

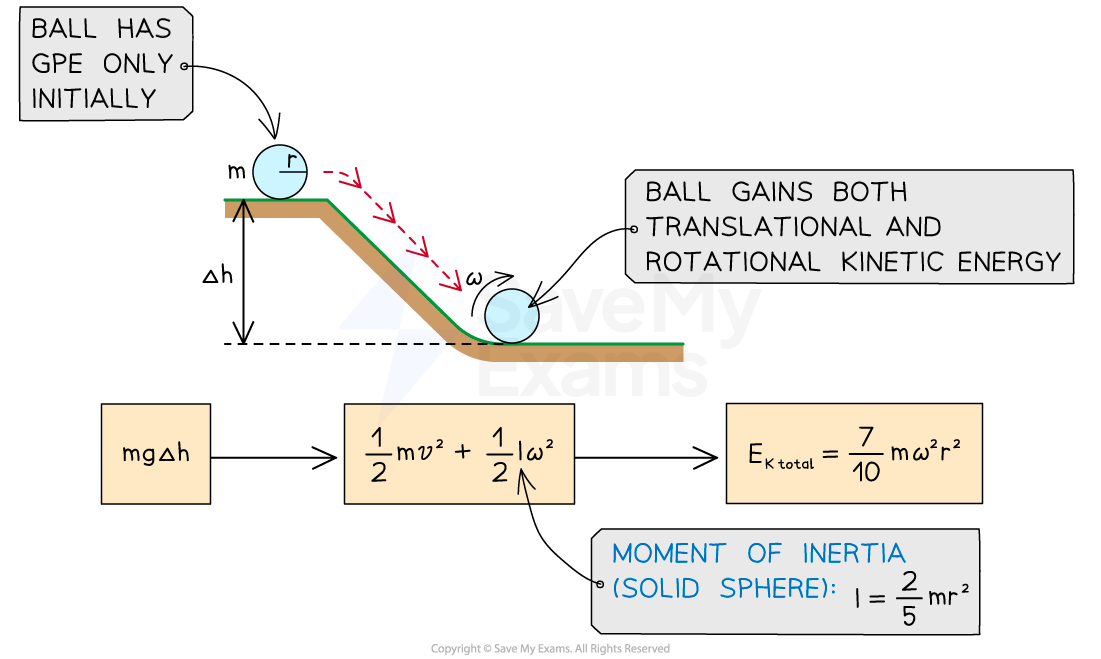
The total kinetic energy acquired by a ball rolling without slipping down a slope is equal to the initial gravitational potential energy at the top of the slope. As it rolls down the slope it gains both translational and rotational kinetic energy — **The gravitational potential energy store of the ball is transferred to the translational and rotational kinetic energy store as it rolls down the slope**

Worked Example

A solid sphere of mass $M$ , radius $R$ , and rotational inertia $I = \frac{2}{5} M R^{2}$ is released from rest at the top of a ramp of height $h$ which makes an angle of $θ$ with the horizontal. Throughout its motion, the sphere rolls without slipping.

(A) Derive an expression for the linear velocity of the center of mass of the sphere at the bottom of the inclined plane in terms of $M$ , $R$ , $θ$ , $h$ and physical constants as appropriate.

(B) Derive an expression for the linear acceleration of the center of mass of the sphere in terms of $M$ , $R$ , $θ$ , $h$ and physical constants as appropriate.

Answer:

Part (A)

Step 1: Analyse the scenario

When an object rolls down the ramp without slipping:
- no work is done by kinetic friction
- the total mechanical energy of the system is conserved
Therefore, the sphere's gravitational potential energy $U_{g}$ at the top of the ramp is completely transferred into kinetic energy $K_{t o t a l}$ at the bottom
The rolling motion indicates the total kinetic energy of the sphere consists of both translational $K_{t r a n s}$ and rotational $K_{r o t}$ components

Step 2: Apply energy conservation laws to the scenario

The total mechanical energy of the system is equal to:

$K_{i} + U_{i} = K_{f} + U_{f}$

Since $K_{i} = U_{f} = 0$ , $U_{i} = ∆ U_{g}$ , and $K_{f} = ∆ K_{t o t a l}$ :

$∆ U_{g} = ∆ K_{t o t a l}$

Step 3: Write expressions for $∆ U_{g}$ and $∆ K_{t o t a l}$

At the top of the ramp, the gravitational potential energy of the stationary sphere is equal to:

$∆ U_{g} = m g ∆ y = M g h$

At the bottom of the ramp, the total kinetic energy of the sphere is equal to:

$∆ K_{t o t a l} = K_{t r a n s} + K_{r o t} = \frac{1}{2} M {v_{c m}}^{2} + \frac{1}{2} I ω^{2}$

Equate the expressions for $∆ U_{g}$ and $∆ K_{t o t a l}$ :

$M g h = \frac{1}{2} M {v_{c m}}^{2} + \frac{1}{2} I ω^{2}$

Substitute the expressions for rotational inertia $I = \frac{2}{5} M R^{2}$ and angular velocity $ω = \frac{v_{c m}}{R}$ into the equation:

$M g h = \frac{1}{2} M {v_{c m}}^{2} + \frac{1}{2} (\frac{2}{5} M R^{2}) {(\frac{v_{c m}}{R})}^{2}$

Step 4: Write the final expression for $v_{c m}$

$M g h = \frac{1}{2} M {v_{c m}}^{2} + \frac{1}{5} M {v_{c m}}^{2}$

$g h = \frac{7}{10} {v_{c m}}^{2}$

$v_{c m} = \sqrt{\frac{10 g h}{7}}$

Part (B)

Step 1: Analyze the scenario

The forces acting on the sphere during its motion are:
- the force of gravity $F_{g}$ acting directly downwards
- the normal force $F_{N}$ acting up and perpendicular to the ramp
- the force of static friction $F_{f}$ acting up and parallel to the ramp

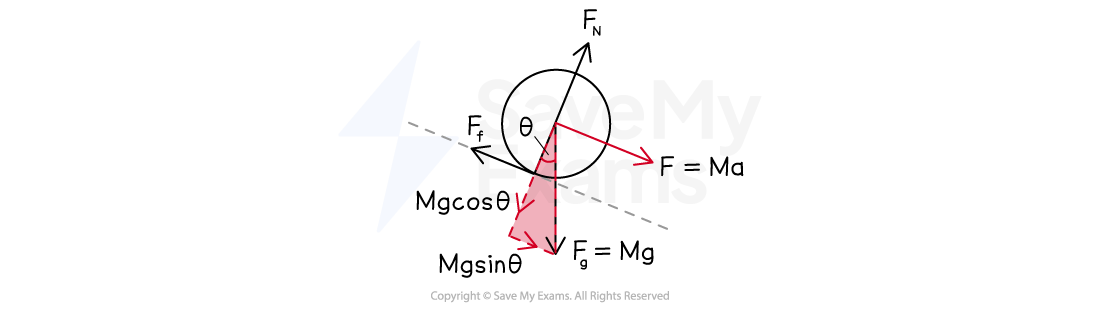
Diagram showing a sphere on an inclined plane with forces labeled: normal force (FN), friction force (Ff), gravitational force (Fg=Mg), and components Mg cosθ and Mg sinθ.

The net torque exerted on the sphere's center of mass is due to the force of static friction only
- This is because it is the only force which does not act directly through the sphere's center of mass
The net force exerted on the sphere's center of mass is proportional to its linear acceleration

Step 2: Write an expression for the frictional force acting on the sphere

Newton's second law in rotational form is given by:

$\sum τ = I α$

The torque due to the frictional force is:

$τ = F r \sin θ = F_{f} R \sin 90 ° = F_{f} R$

Substitute the expressions for rotational inertia $I = \frac{2}{5} M R^{2}$ and angular acceleration $α = \frac{a_{c m}}{R}$ into the equation:

$F_{f} R = (\frac{2}{5} M R^{2}) (\frac{a_{c m}}{R})$

Therefore, the frictional force acting on the sphere is:

$F_{f} = \frac{2}{5} M a_{c m}$

Step 3: Write an expression for the net force exerted on the sphere

The net force, and therefore, the linear acceleration of the sphere act down and parallel to the ramp
Newton's second law is given by:

$\sum F = M a_{c m}$

Two forces act parallel to the ramp, in opposite directions, these are:
- a component of the gravitational force (weight): $M g \sin θ$
- the frictional force $F_{f}$
The net force on the sphere is therefore equal to:

$M g \sin θ - F_{f} = M a_{c m}$

Step 4: Write the final expression for $a_{c m}$

$M g \sin θ - \frac{2}{5} M a_{c m} = M a_{c m}$

$M g \sin θ = \frac{7}{5} M a_{c m}$

$a_{c m} = \frac{5}{7} g \sin θ$

Examiner Tips and Tricks

The equation for translational displacement $Δ x_{c m} = r Δ θ$ is given on your equation sheet, but the equations for $v_{c m}$ and $a_{c m}$ are not.

However, the equations for $v_{c m}$ and $a_{c m}$ have the same form as their tangential forms, and these are given on the equation sheet. Furthermore, both can easily be derived by dividing the $Δ x_{c m}$ equation by time. Similarly, dividing the equation for $v_{c m}$ by time gives the equation for $a_{c m}$ .

Rolling while slipping

When a rigid body rolls while slipping, the translational motion of the system's center of mass cannot be directly related to its rotational motion

$∆ x_{c m} \neq r ∆ θ$

$v_{c m} \neq r ω$

$a_{c m} \neq r α$

This is because the point of contact between the rotating body and the surface is not at rest
In the case of rolling motion while slipping:
- there is not enough static friction to cause the rotation about the system's center of mass
- only kinetic friction is present as there is relative motion between the surface and the point of contact
As with the no-slipping case, the direction of the frictional force acts to oppose the slipping motion

Since work is done by kinetic friction, energy is dissipated from the system when slipping occurs
The amount of energy dissipation (work done) depends on
- the coefficient of kinetic friction
- the distance over which slipping occurs

Examiner Tips and Tricks

You will not be expected to quantitively explain the relationships between linear and angular quantities for an object rolling while slipping, as these are beyond the scope of both AP Physics 1 and 2.

However, you may be expected to qualitatively explain the changes to linear and angular quantities for a rigid body rolling while slipping.

You may also come across questions where a rigid body is released from the top of a frictionless slope, be aware that this results in slipping, but neither static nor kinetic frictional forces are acting in this scenario, so this results in purely translational motion.

You may come across the term 'rolling friction' in your studies, but rest assured this is beyond the scope of AP Physics 1 and will not be tested.

Last updated: 23 October 2024

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself

Did this page help you?

Previous:Angular Momentum of a SystemNext:Motion of Orbiting Satellites

Rolling (College Board AP® Physics 1: Algebra-Based)

Study Guide

Total kinetic energy

Rolling without slipping

Translational and rotational components of a rotating wheel

The role of friction in rolling without slipping

Static friction causing rolling on a horizontal plane

Static friction causing rolling on an inclined plane

Rolling on a horizontal surface without slipping

Rolling on an inclined plane without slipping

Worked Example

Examiner Tips and Tricks

Rolling while slipping

Examiner Tips and Tricks

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Katie M

Author: Caroline Carroll