Study GuidesExam QuestionsPast Papers
AP®PhysicsCollege BoardPhysics 1: Algebra-BasedStudy GuidesUnit 6: Energy & Momentum of Rotating SystemsExamples of Rotational SystemsMotion of Orbiting Satellites

Motion of Orbiting Satellites (College Board AP® Physics 1: Algebra-Based): Study Guide

Katie M

Written by: Katie M

Reviewed by: Caroline Carroll

Updated on

Motion of orbiting satellites

  • When a system consists only of a satellite orbiting a massive central object:

    • the mass of the orbiting satellite is considered negligible (compared to the mass of the central object)

    • both bodies orbit around a single center of mass, but the central object is considered stationary

  • Satellites can be categorized as natural satellites or artificial satellites

  • Examples of satellite-central-object systems include:

    • planets or comets orbiting the Sun

    • moons or spacecraft orbiting a planet

Gravitational potential energy of a system

  • Gravitational potential energy is the energy possessed by an object due to its position in a gravitational field

  • The gravitational potential energy of a system is defined as:

The work done to assemble the system from infinite separation of the components of the system

  • Gravitational potential energy is calculated using the following equation:

U subscript g space equals space minus G fraction numerator m subscript 1 m subscript 2 over denominator r end fraction

  • Where:

    • U subscript g = gravitational potential energy of the system, in straight J

    • G = universal gravitational constant open parentheses 6.67 cross times 10 to the power of negative 11 end exponent space straight N times straight m squared divided by kg squared close parentheses

    • m subscript 1 = mass of the central body, in kg

    • m subscript 2 = mass of the orbiting satellite, in kg

    • r = distance between the centers of the masses, in straight m

  • For a satellite-central-object system:

    • potential energy is defined as zero when the satellite is an infinite distance from the central object

    • potential energy increases when the distance of the satellite from the central object increases

    • potential energy decreases when the distance of the satellite from the central object decreases

Diagram showing a satellite's potential energy change due to gravity. Positive ΔU increases potential energy as the satellite moves away, negative ΔU decreases it as it moves closer. Satellite orbits around Earth.
Work is done on a satellite to move it further away from the Earth, as gravity is attractive. This increases the gravitational potential energy of the system. Conversely, work is done by the satellite to move it closer to the Earth.

Energy of an orbiting satellite

  • Gravity is a conservative force, therefore, the total energy of a satellite-central-object system is constant

  • The total mechanical energy is equal to the sum of the system's kinetic and potential energies:

Total mechanical energy = kinetic energy + gravitational potential energy

E subscript t o t a l end subscript space equals space K space plus thin space U

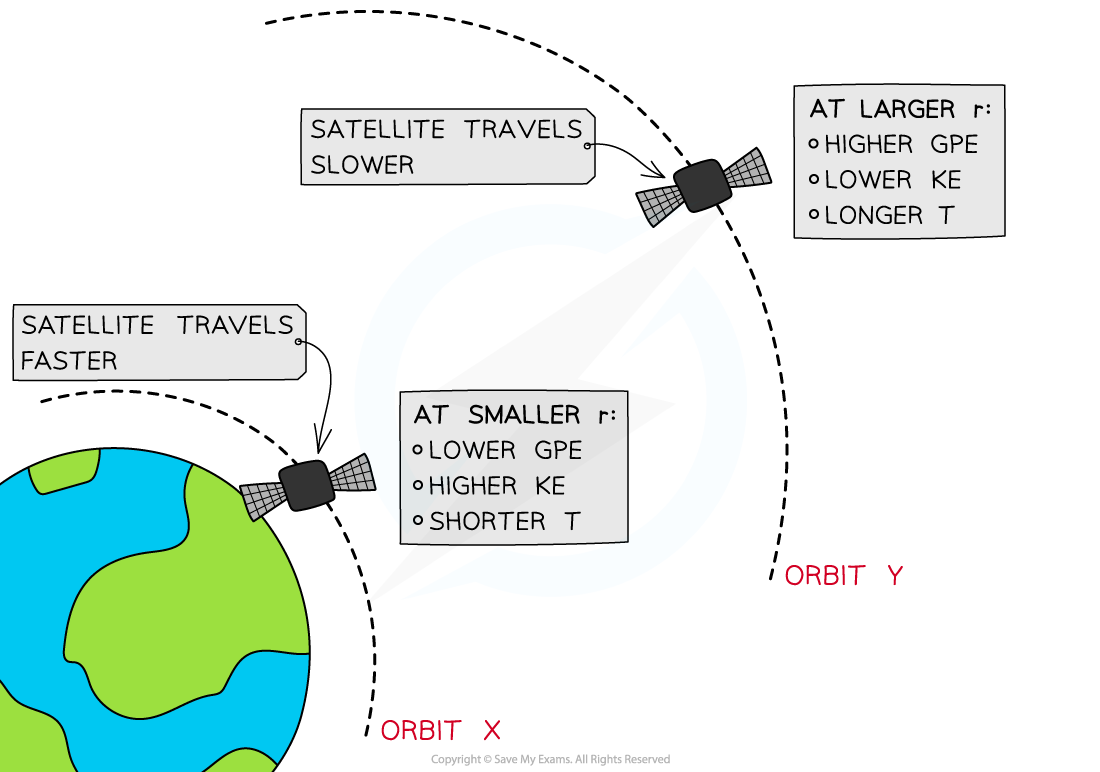
  • A satellite moving in a circular orbit of fixed orbital radius has a constant orbital speed

  • Therefore, the satellite's kinetic and potential energies are also constant for a particular orbital radius

  • To change the orbital radius of a satellite, work must be done, which means that:

    • if the orbital radius of the satellite decreases then E subscript t o t a l end subscript decreases, K increases, and U decreases

    • if the orbital radius of the satellite increases then E subscript t o t a l end subscript increases, K decreases, and U increases

Variation of energy with orbital radius

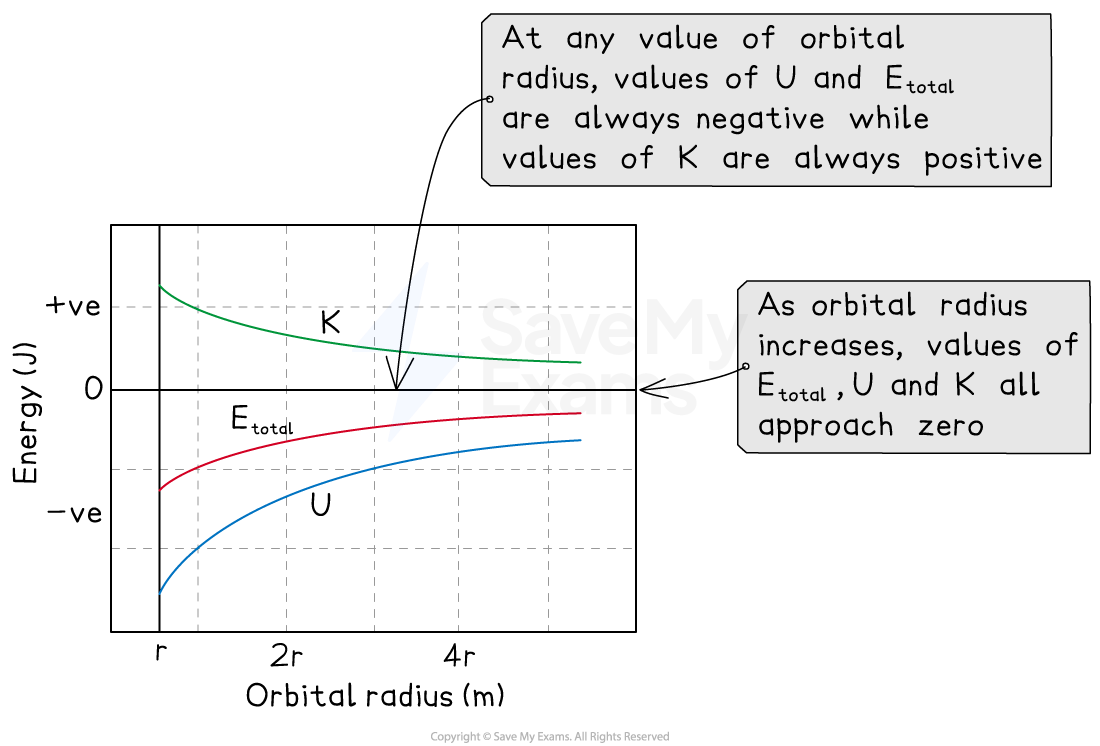
Graph showing energy versus orbital radius. K (green) is positive and decreases, U (blue) is negative and increases, and E_total (red) is negative and increases.
At a specified orbital radius, the values of total energy, kinetic energy and potential energy are constant for a satellite in a circular orbit. These values decrease as distance from the central body increases

Comparing energies of satellites in different orbits

Diagram showing satellite speeds and properties in different orbits. Satellite travels faster in low orbit with higher KE and lower GPE. It travels slower in high orbit.
The satellite in the higher orbit (Y) has a greater GPE and moves slower due to having a lower KE than the satellite in the lower orbit (X)

Circular and elliptical orbits

  • The path of an orbiting satellite around a central object may be circular or elliptical

  • In both types of orbit, the total energy and the total angular momentum of the system are constant throughout the satellite's motion

Analyzing circular orbits

  • In a circular orbit, the satellite's speed and radius are constant, which means:

    • the system's total mechanical energy and the gravitational potential energy are constant

    • the satellite's angular momentum, kinetic energy, and speed are constant

Satellite in a circular orbit

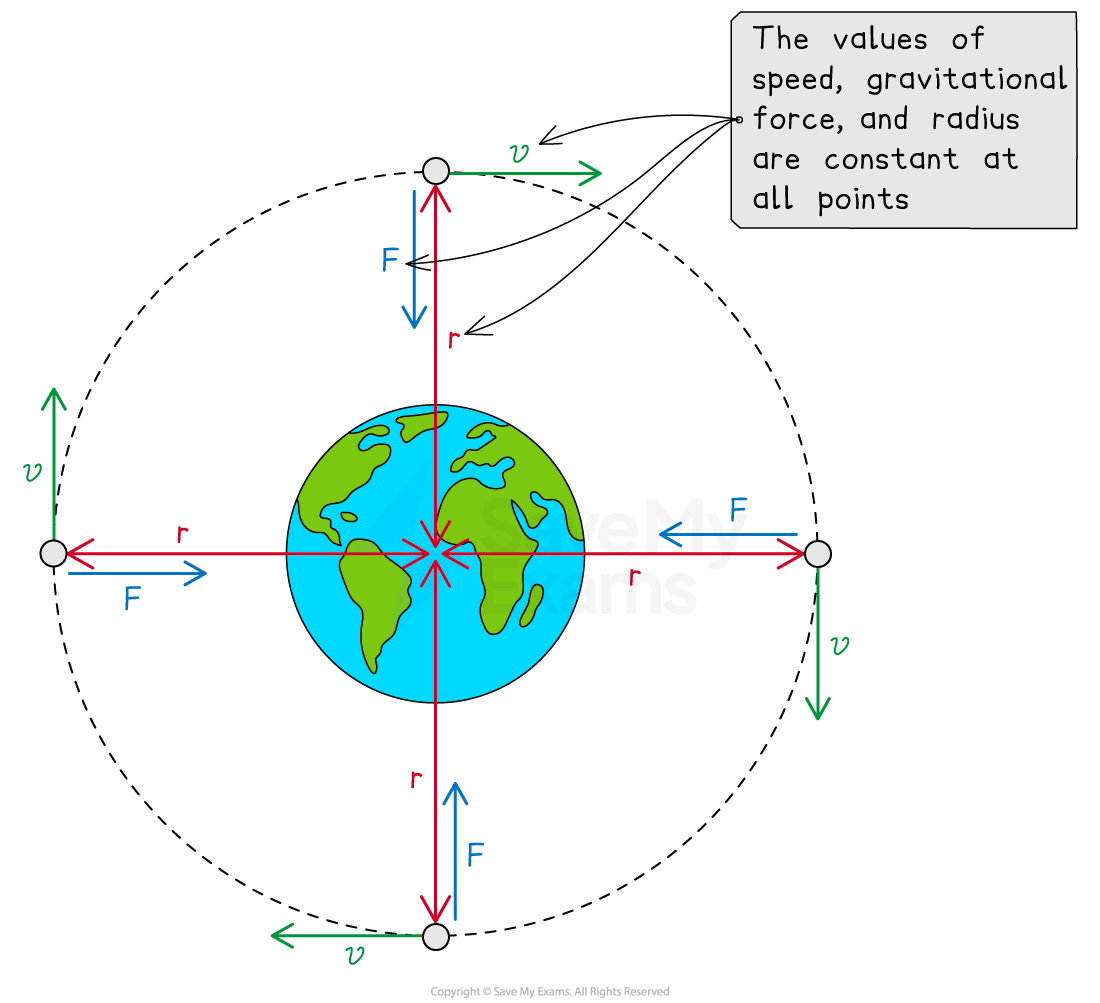
Diagram of a satellite orbiting Earth in a circular orbit. Labels indicate constant speed (v), gravitational force (F), and radius (r) from Earth at all points. Text box reads: "the values of speed, gravitational force, and radius are constant at all points."
In circular orbits, the system’s total mechanical energy, gravitational potential energy, and the satellite’s angular momentum and kinetic energy are constant

Orbital speed of a satellite

  • A satellite’s orbit is maintained by the force of gravitational attraction, F subscript g, between the satellite and the central object

  • In a circular orbit, this force acts towards the center of the circular path as a centripetal force, F subscript c

F subscript g space equals space F subscript c

fraction numerator G M m over denominator r squared end fraction space equals space fraction numerator m v squared over denominator r end fraction

  • Where:

    • G = universal gravitational constant open parentheses 6.67 cross times 10 to the power of negative 11 end exponent space straight N times straight m squared divided by kg squared close parentheses

    • M = mass of the central body, in kg

    • m = mass of the orbiting satellite, in kg

    • v = orbital speed of the satellite, in straight m divided by straight s

    • r = distance between the centers of the masses, in straight m

  • Therefore, the orbital speed of a satellite is:

v space equals space square root of fraction numerator G M over denominator r end fraction end root

  • This means that all satellites, regardless of their mass, will travel at the same speed v in a circular orbit of radius r

Angular momentum of a satellite

  • When traveling in a circular path, the radius and the velocity of the satellite are always perpendicular to each other

  • The angular momentum of the orbiting satellite is:

L space equals space m v r space sin space 90 degree space equals space m v r

L space equals space m r square root of fraction numerator G M over denominator r end fraction end root space equals space m square root of G M r end root

  • This means that the angular momentum of a satellite traveling in a circular orbit of radius r is constant

Total energy of a circular orbit

  • The total mechanical energy of the system is the sum of kinetic and potential energies:

E subscript t o t a l end subscript space equals space K space plus space U

E subscript t o t a l end subscript space equals space 1 half m v squared space minus space fraction numerator G M m over denominator r end fraction

  • Substituting the equation for orbital speed:

E subscript t o t a l end subscript space equals space 1 half m open parentheses fraction numerator G M over denominator r end fraction close parentheses space minus space fraction numerator G M m over denominator r end fraction

E subscript t o t a l end subscript space equals space fraction numerator G M m over denominator 2 r end fraction space minus space fraction numerator G M m over denominator r end fraction

E subscript t o t a l end subscript space equals space minus fraction numerator G M m over denominator 2 r end fraction

  • Therefore, for a circular orbit, the following apply at all points:

    • K space equals space minus 1 half U

    • E subscript t o t a l end subscript space equals space 1 half U space equals space minus K

Analyzing elliptical orbits

  • In an elliptical orbit, the satellite's speed and radius are not constant, which means:

    • the system’s total mechanical energy and the satellite’s angular momentum are constant

    • the system’s gravitational potential energy and the satellite’s kinetic energy change throughout the satellite's motion

Satellite in an elliptical orbit

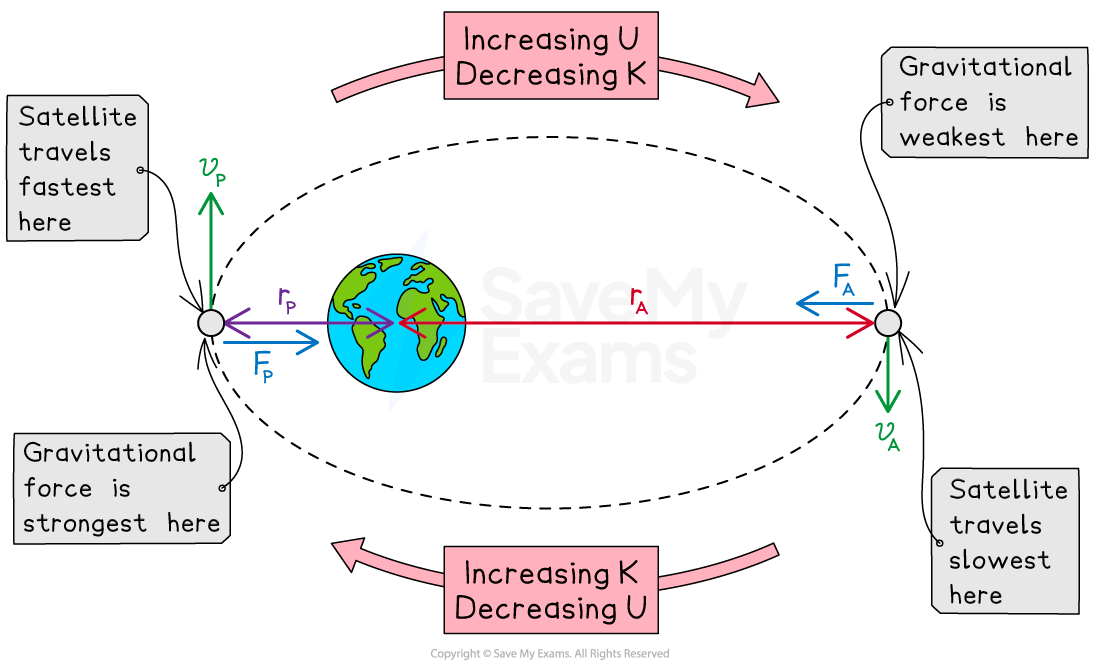
Diagram of a satellite's elliptical orbit around Earth. When the satellite is at the point closest to the Earth, it travels fastest and the gravitational force is strongest here. When the satellite is at the point farthest from the Earth, it travels slowest and the gravitational force is weakest here. Top label indicates potential energy U increases and kinetic energy K decreases when moving away from Earth. Bottom label indicates kinetic energy K increases and potential energy U decreases when moving toward the Earth.
In elliptical orbits, the system’s total mechanical energy and the satellite’s angular momentum are constant, but the system’s gravitational potential energy and the satellite’s kinetic energy can each change

Angular momentum of a satellite

  • When traveling in an elliptical path, the angle between the radius and the velocity of the satellite changes

  • The angular momentum of the orbiting satellite is:

L space equals space m v r space sin space theta

  • Where:

    • theta = angle between the radius and the velocity of the satellite, in degree

  • As with a circular orbit, the gravitational attraction between the satellite and the central object is the only force that acts on the system

    • This force acts towards the focus of the ellipse where the central body is located

    • Since this force always acts in the same direction as the radius, it can never cause a torque open parentheses tau space equals space F r space sin space 0 space equals space 0 close parentheses

  • Therefore, the angular momentum of the satellite is constant as no net external torque acts on the satellite-central-object system

Orbital speed of a satellite

  • To conserve angular momentum, the satellite reaches maximum and minimum values of radius and velocity at the two extreme points

  • At the point closest to the central object:

    • the radial distance is the shortest

    • the satellite has the highest speed

  • At the point farthest from the central object:

    • the radial distance is the greatest

    • the satellite has the lowest speed

Total energy of an elliptical orbit

  • To conserve mechanical energy, the satellite reaches maximum and minimum values of kinetic energy and gravitational potential energy at the two extreme points

  • At the point closest to the central object:

    • the satellite has the highest kinetic energy

    • the system has the lowest (most negative) gravitational potential energy

  • At the point farthest from the central object:

    • the satellite has the lowest kinetic energy

    • the system has the highest (least negative) gravitational potential energy

Worked Example

A satellite in an elliptical orbit around a planet has speed v subscript 1 at its closest distance from the center of the planet r subscript 1 and speed v subscript 2 at its farthest distance from the center of the planet r subscript 2.

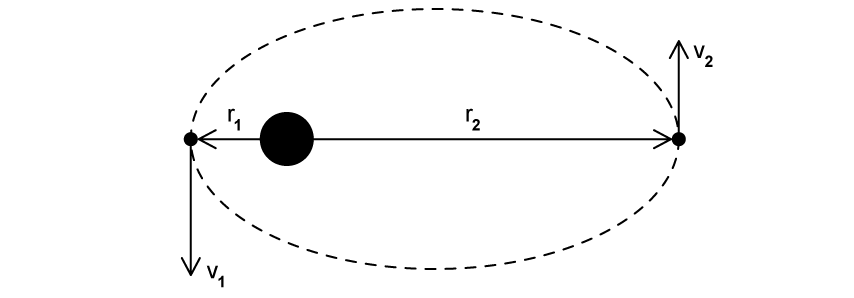
Diagram of an elliptical orbit showing two velocities, v1 and v2, and radii, r1 and r2, with a central black circle representing a celestial body.

Which of the following expressions correctly represents v subscript 2?

A      v subscript 2 space equals space r subscript 1 over r subscript 2 v subscript 1

B      v subscript 2 space equals space r subscript 2 over r subscript 1 v subscript 1

C      v subscript 2 space equals space fraction numerator r subscript 1 plus r subscript 2 over denominator 2 end fraction v subscript 1

D      v subscript 2 space equals space fraction numerator r subscript 1 minus r subscript 2 over denominator r subscript 1 plus r subscript 2 end fraction v subscript 1

The correct answer is A

Answer:

Step 1: Determine the angular momentum of the satellite at the two extreme points

  • The angular momentum of the orbiting satellite is:

L space equals space m v r space sin space theta

  • At its closest distance to the planet, the angular momentum is

L subscript 1 space equals space m v subscript 1 r subscript 1 space sin space 90 degree space equals space m v subscript 1 r subscript 1

  • At its farthest distance from the planet, the angular momentum is

L subscript 2 space equals space m v subscript 2 r subscript 2 space sin space 90 degree space equals space m v subscript 2 r subscript 2

Step 2: Apply conservation of angular momentum

  • The satellite's angular momentum is constant at all points in its orbit, so:

L subscript 1 space equals space L subscript 2

m v subscript 1 r subscript 1 space space equals space m v subscript 2 r subscript 2

v subscript 1 r subscript 1 space equals space v subscript 2 r subscript 2

Step 3: Write an expression for the speed of the satellite at the furthest point

v subscript 2 space equals space r subscript 1 over r subscript 2 v subscript 1

  • Note: This relationship between speed and radial distance can be applied at any point in the orbit

Diagram of an elliptical orbit around Earth, showing velocities and distances at two positions. Equation: v1/v2 = r2/r1. Position 1 with v1 and r1; Position 2 with v2 and r2.

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:RollingNext:Escape Velocity
    Author
    Reviewer
    Katie M

    Author: Katie M

    Expertise: Physics

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.

    Caroline Carroll

    Author: Caroline Carroll

    Expertise: Physics Subject Lead

    Caroline graduated from the University of Nottingham with a degree in Chemistry and Molecular Physics. She spent several years working as an Industrial Chemist in the automotive industry before retraining to teach. Caroline has over 12 years of experience teaching GCSE and A-level chemistry and physics. She is passionate about creating high-quality resources to help students achieve their full potential.