Escape Velocity (College Board AP® Physics 1: Algebra-Based)

Escape velocity

• To escape the gravitational field of a central body, a satellite must travel at, or above, a minimum escape velocity

  • This is dependent on the mass and radius of the central body creating the gravitational field

  • Examples of central bodies include planets, moons, or even black holes

• Escape velocity is defined as:

The minimum velocity that will allow an object to escape a gravitational field with no further energy input

• The escape velocity of a satellite is such that the mechanical energy of the satellite–central-object system is equal to zero

• If a satellite reaches escape velocity, it will:

  • move away from the central body

  • have a velocity of zero at an infinite distance from the central body

• This is assuming that the only force exerted on the satellite is the gravitational attraction of the central object

Escape velocity of the Earth

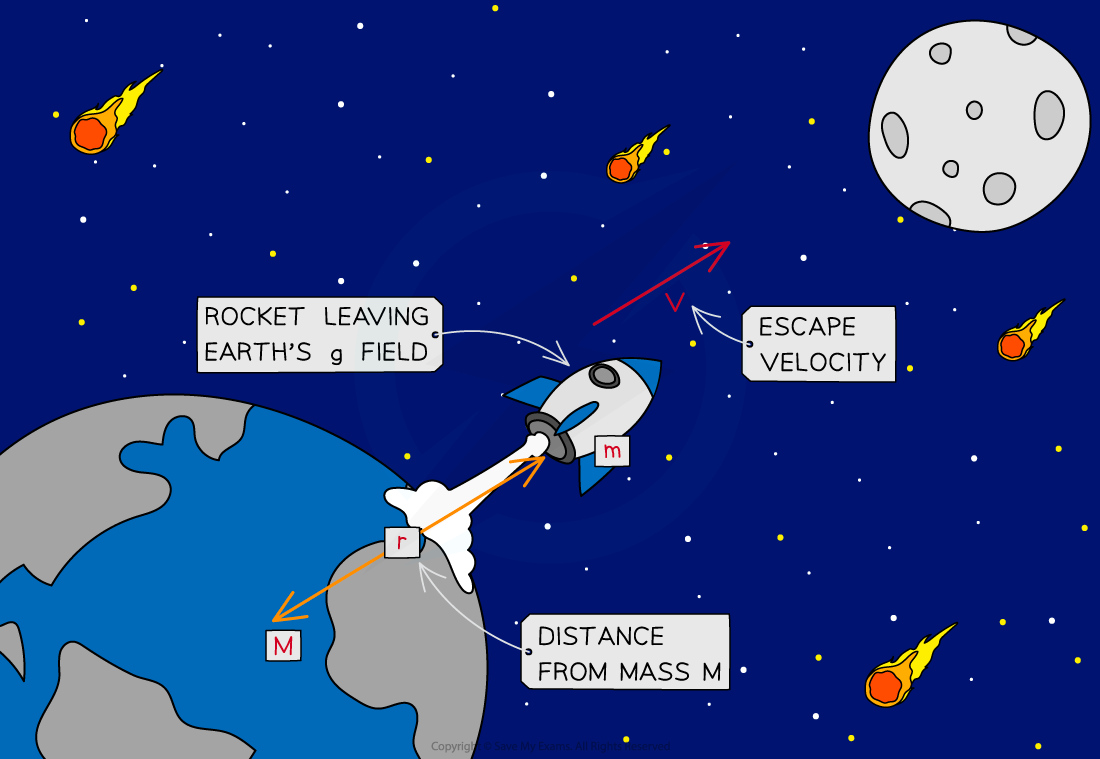
• Rockets launched from the Earth's surface do not need to achieve escape velocity to reach an orbit

  • This is because the orbit would still be within Earth's gravitational field

  • Therefore, less work would be required to move to this position than to escape the Earth's gravitational field entirely

Derived equation

• The escape velocity of a satellite from a central body of mass is:

• This equation can be derived using energy conservation laws

Step 1: Identify the fundamental equations

• The kinetic energy of a satellite is:

• The gravitational potential energy of a satellite is:

• Where:

  • = mass of the satellite, in

  • = escape velocity of the satellite, in

  • = Universal gravitational constant

  • = mass of the central object, in

  • = distance between the satellite and the center of the central object, in

Step 2: Apply the specific conditions

• The escape speed of a satellite is the speed at which all its kinetic energy has been transferred to gravitational potential energy

• Since mass is the same on both sides of the equation, it cancels out:

• Multiplying both sides by 2 and taking the square root gives the following equation:

• This equation shows that escape velocity is the same for all masses occupying the same gravitational field

  • For example, on Earth, the value of escape velocity is the same for both a satellite and a tennis ball