Conservation of Angular Momentum (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself

Author

Katie M

Expertise

Physics

Conservation of angular momentum

As with linear momentum, angular momentum is always conserved
The principle of conservation of angular momentum states:

The total angular momentum of an isolated system remains constant unless acted on by a net external torque

Therefore, for an interaction between objects in an isolated system:

The total angular momentum before the interaction is equal to the total angular momentum after the interaction

Mathematically, this can be written as:

$\sum L_{i} = \sum L_{f}$

Where:
- $L_{i}$ = initial angular momentum (before the interaction), in $kg \cdot m^{2} / s$
- $L_{f}$ = final angular momentum (after the interaction), in $kg \cdot m^{2} / s$

Worked Example

A bicycle tire of mass $M$ and radius $R$ is mounted horizontally, allowing it to spin about a frictionless axis. The tire is initially at rest before a dart of mass $m$ strikes it with velocity $v$ at an angle of $θ$ as shown in the diagram.

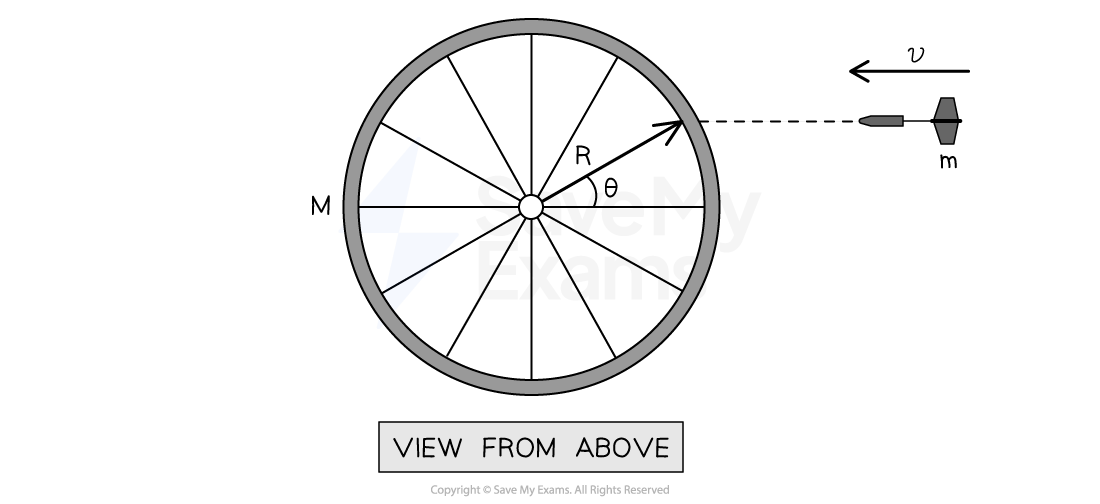
Diagram showing a top-down view of a wheel with mass M, radius R, and an arrow at angle θ to the radius. A dart of mass m moves tangentially with velocity v.

The rotational inertia of the dart and wheel is $(m + M) R^{2}$ .

Derive an expression for the angular velocity of the tire after the dart strikes it in terms of $m$ , $M$ , $R$ and $θ$ .

Answer:

Step 1: Analyze the scenario

Before the collision:
- the tire of mass $M$ is stationary
- the dart of mass $m$ moves with linear velocity $v$
After the collision:
- the tire and dart move as one rigid body of rotational inertia $(m + M) R^{2}$ and angular velocity $ω$

Step 2: Determine the angular momentum of the dart

Just before the dart strikes the tire
- it is located at a distance of $R$ from the axis of rotation
- its velocity makes an angle of $θ$ with this distance
Therefore, using the equation for a particle's angular momentum, the dart can be modeled as a particle with an initial angular momentum of:

$L_{i} = m v R \sin θ$

Step 3: Determine the angular momentum of the dart-tire system

When the dart strikes the tire, they become one system with an angular momentum of:

$L_{f} = I ω = (m + M) R^{2} ω$

Step 4: Apply conservation of angular momentum

Conservation of angular momentum: the total angular momentum before the collision = the total angular momentum after the collision

$\sum L_{i} = \sum L_{f}$

$m v R \sin θ = (m + M) R^{2} ω$

Step 5: Rearrange for the angular velocity $ω$

$ω = \frac{m v R \sin θ}{(m + M) R^{2}} = \frac{m v \sin θ}{(m + M) R}$

Angular impulse & total angular momentum

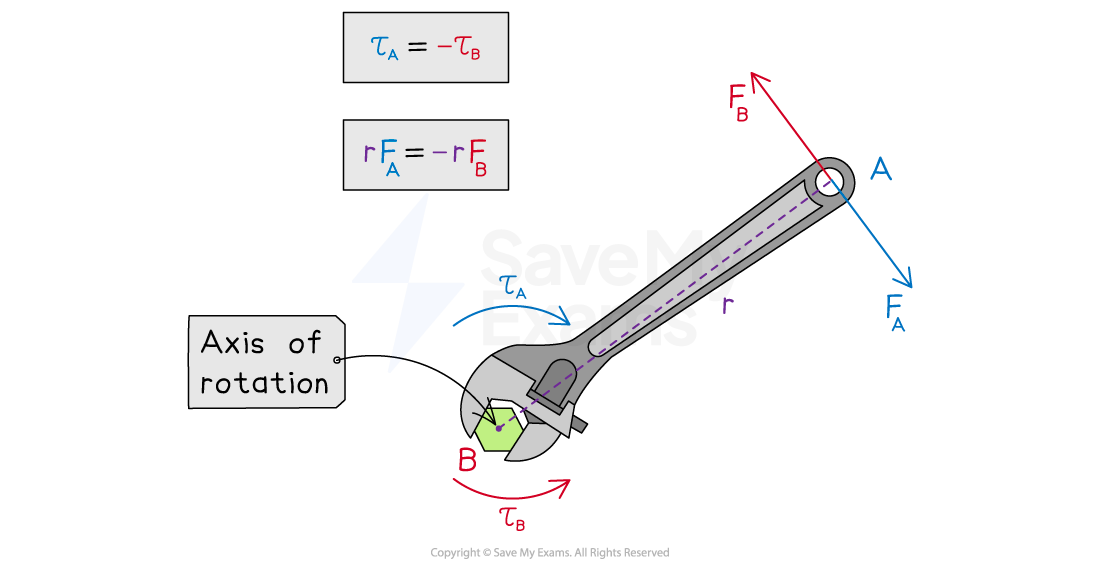
Conservation of angular momentum is a direct result of Newton's third law, which states:

The angular impulse exerted by object (or system) A on object (or system) B is equal and opposite to the angular impulse exerted by object (or system) B on object (or system) A

If the total angular momentum of a system changes, that change is equivalent to the angular impulse exerted on the system

$angular impulse = ∆ L$

Where:
- angular impulse is measured in $N \cdot m \cdot s$
- $∆ L$ = change in angular momentum of the system, in $kg \cdot m^{2} / s$
When two objects, A and B, rotating about the same axis interact:
- object A exerts a torque on object B of magnitude $τ_{A}$
- object B exerts a torque on object A of magnitude $τ_{B}$
- the torques are equal in magnitude and opposite in direction $τ_{A} = - τ_{B}$
- the torques, and therefore angular impulses, only act for the duration of the interaction
Since the angular impulse is delivered during the interaction, the value of time $∆ t$ is equal for each object, hence the change in momentum is:

$∆ L = τ ∆ t$

Therefore, the change in angular momentum of A is equal to the change in angular momentum of B:

$∆ L_{A} = - ∆ L_{B}$

Third law torque pair during an interaction

Diagram of a wrench and bolt demonstrating Newton's third law for torque.
When a torque τA is exerted by a wrench on a bolt, the bolt exerts an equal torque τB on the wrench in the opposite direction. This is equivalent to the corresponding forces acting at a distance r from the axis of rotation. — According to Newton's third law, the torque exerted by object A (the wrench) on object B (the bolt) is equal to the torque exerted by B on A and opposite in direction. This is equivalent to the corresponding forces acting at a distance r from the axis of rotation

Examiner Tip

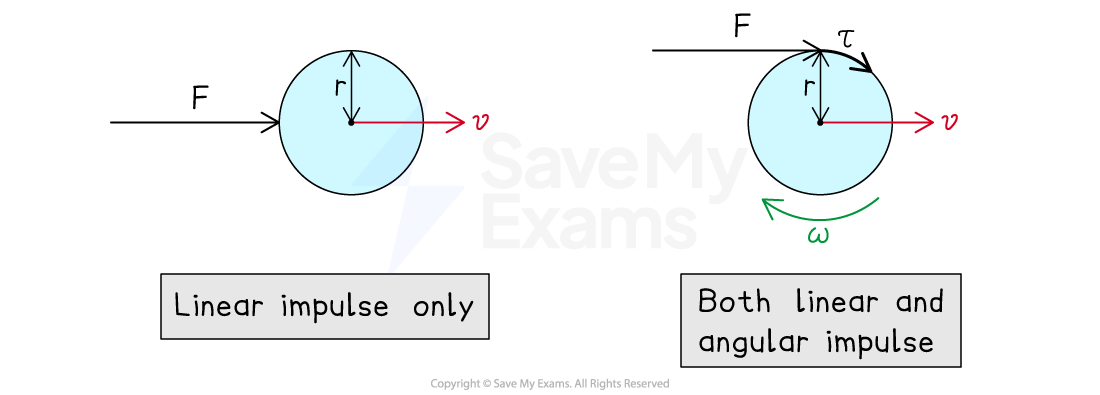
Make sure you understand that Newton's third law in rotational form only applies when a force is applied at a distance $r$ from a rotational axis. As a result, the Newton's third law force pair acts at the same point (i.e. at a distance $r$ ). For example, consider a sphere:

when a force is exerted along its rotational axis, only a linear impulse will act about its center of mass
when a force is exerted along its circumference (i.e. a distance $r$ from its rotational center), both a linear impulse and an angular impulse will act about its center of mass

Left: When a force is applied along the center of mass of a sphere, it produces linear impulse only as there is no rotation
Right: When a force is applied along the circumference of a sphere, it produces both linear and angular impulse as there is rotation

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Next topic

Did this page help you?