Angular Momentum of a System (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself

Author

Katie M

Expertise

Physics

Angular speed of a nonrigid system

As a result of the principle of conservation of angular momentum, when a nonrigid system changes shape, it may increase or decrease its angular speed
There are several real-world examples of this, such as:
- a person on a spinning chair spins faster when their arms and legs are contracted and slower when extended
- ice skaters can change their rotational velocity by extending or contracting their arms
- tornados spin faster as their radius decreases
When a nonrigid system changes its shape, the distribution of mass about its rotational axis may also change
- This results in a change to its rotational inertia
Angular momentum is the product of rotational inertia and angular speed $(L = I ω)$
- Therefore, if rotational inertia changes, angular speed must change to conserve angular momentum

A nonrigid system may change its shape by
- moving mass closer to the rotational axis, thereby decreasing the rotational inertia of the system
- moving mass further from the rotational axis, thereby increasing the rotational inertia of the system

Conservation of angular momentum in a nonrigid system

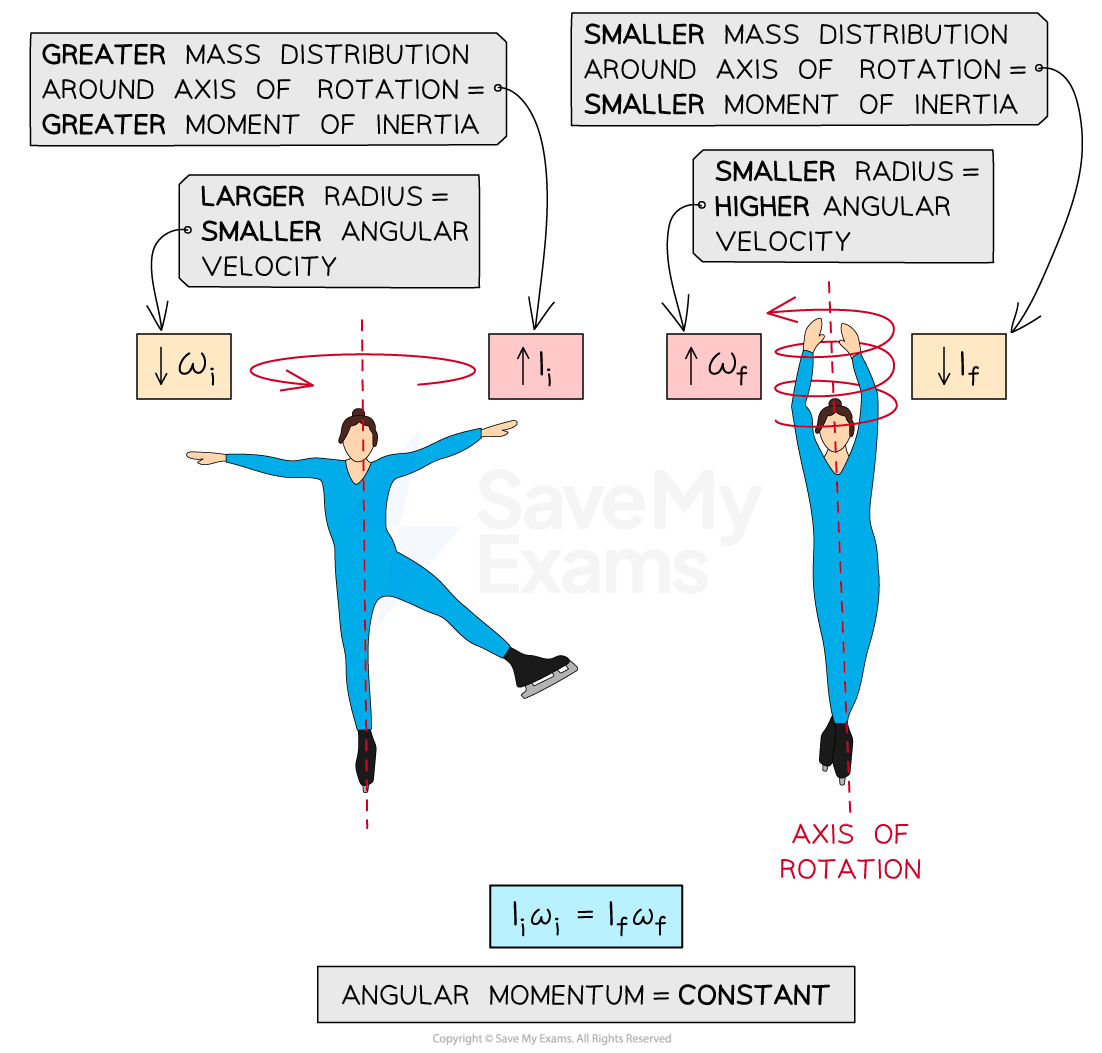
An ice skater with arms extended and contracted, illustrating angular momentum conservation.
When their arms are extended: greater mass distribution around their axis of rotation equates to a greater rotational inertia and a larger radius equates to a smaller angular velocity.
When their arms are contracted: smaller mass distribution around their axis of rotation equates to a smaller rotational inertia and a smaller radius equates to a higher angular velocity. — **Ice skaters can change their rotational inertia by extending or contracting their arms and legs. Due to conservation of angular momentum, this allows them to spin faster or slower**

In a nonrigid system where no external torque acts, the angular momentum of the system remains constant
Due to the conservation of angular momentum, the angular speed of a nonrigid system will:
- increase to compensate for a change in shape which decreases the rotational inertia of the system
- decrease to compensate for a change in shape which increases the rotational inertia of the system

Therefore, for a constant angular momentum, the following equation can be used:

$I_{i} ω_{i} = I_{f} ω_{f}$

Where:
- $I_{i}$ = initial rotational inertia, in $kg \cdot m^{2}$
- $ω_{i}$ = initial angular velocity, in $rad / s$
- $I_{f}$ = final rotational inertia, in $kg \cdot m^{2}$
- $ω_{f}$ = final angular velocity, in $rad / s$

Total angular momentum of a system

Total angular momentum

The total angular momentum of a system about a rotational axis is the sum of the angular momenta of the system’s constituent parts about that axis

$L = \sum_{i} L_{i} = \sum_{i} (m_{i} v_{i} r_{i})$

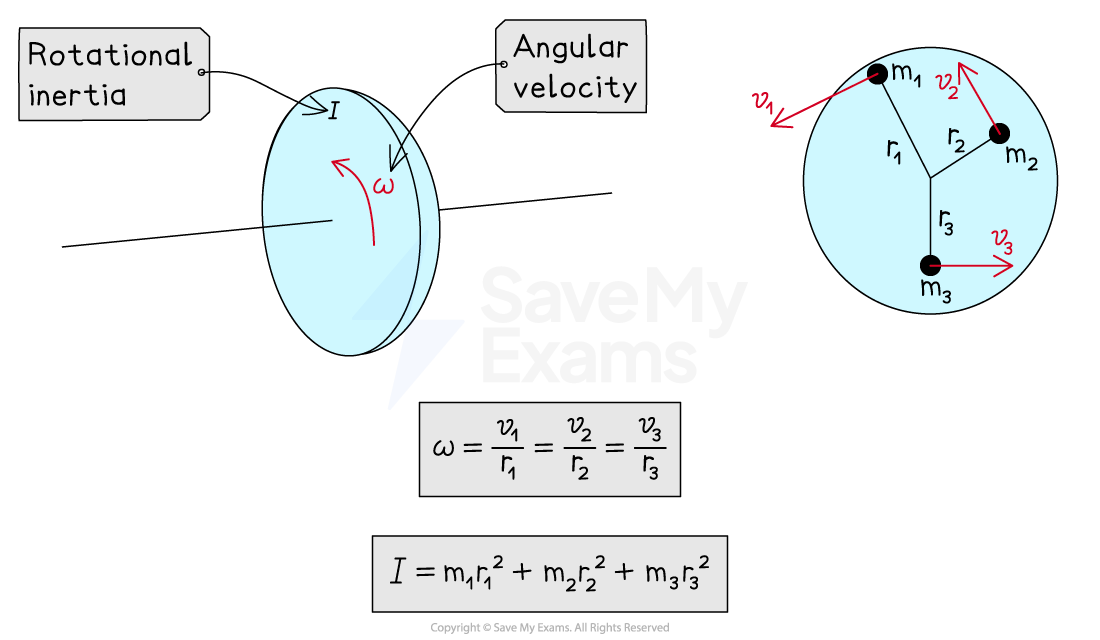
Diagram illustrating rotational inertia and angular velocity of a rotating object, showing radial velocities v1, v2, v3, and formulas for ω and rotational inertia I. — **The total angular momentum of a system can be broken down into the constituent particles of mass m, velocity v and distance from the rotational axis r**

Total angular speed

Each particle has a different linear velocity $v_{i}$ depending on its distance $r_{i}$ from the rotational axis
- Note: assuming the $\vec{v}$ and $\vec{r}$ vectors are perpendicular to each other
The overall system can therefore be described by an angular velocity equal to:

$ω = \frac{v_{i}}{r_{i}}$

Total rotational inertia

Each particle of mass $m_{i}$ contributes to the overall mass distribution of the system depending on its distance $r_{i}$ from the rotational axis
The overall system can therefore be described by a rotational inertia equal to:

$I = \sum_{i} (m_{i} {r_{i}}^{2})$

Deriving the equation for angular momentum

Therefore, a collection of objects with individual angular momenta can be described as one system with an associated angular velocity and rotational inertia about a specified axis

$L = \sum_{i} (m_{i} v_{i} r_{i}) = \sum_{i} (m_{i} r_{i}) (r_{i} ω) = ω \sum_{i} (m_{i} {r_{i}}^{2})$

We can then simplify the expression to give us the expression for the total angular momentum of the system:

$L = I ω$

Where:
- $L$ = total angular momentum of the system, in $kg \cdot m^{2} / s$
- $I$ = total rotational inertia of the system, in $kg \cdot m^{2}$
- $ω$ = angular velocity about the rotational axis of the system, in $rad / s$

Worked Example

The diagram shows the different positions of a diver between jumping off a springboard and entering the water.

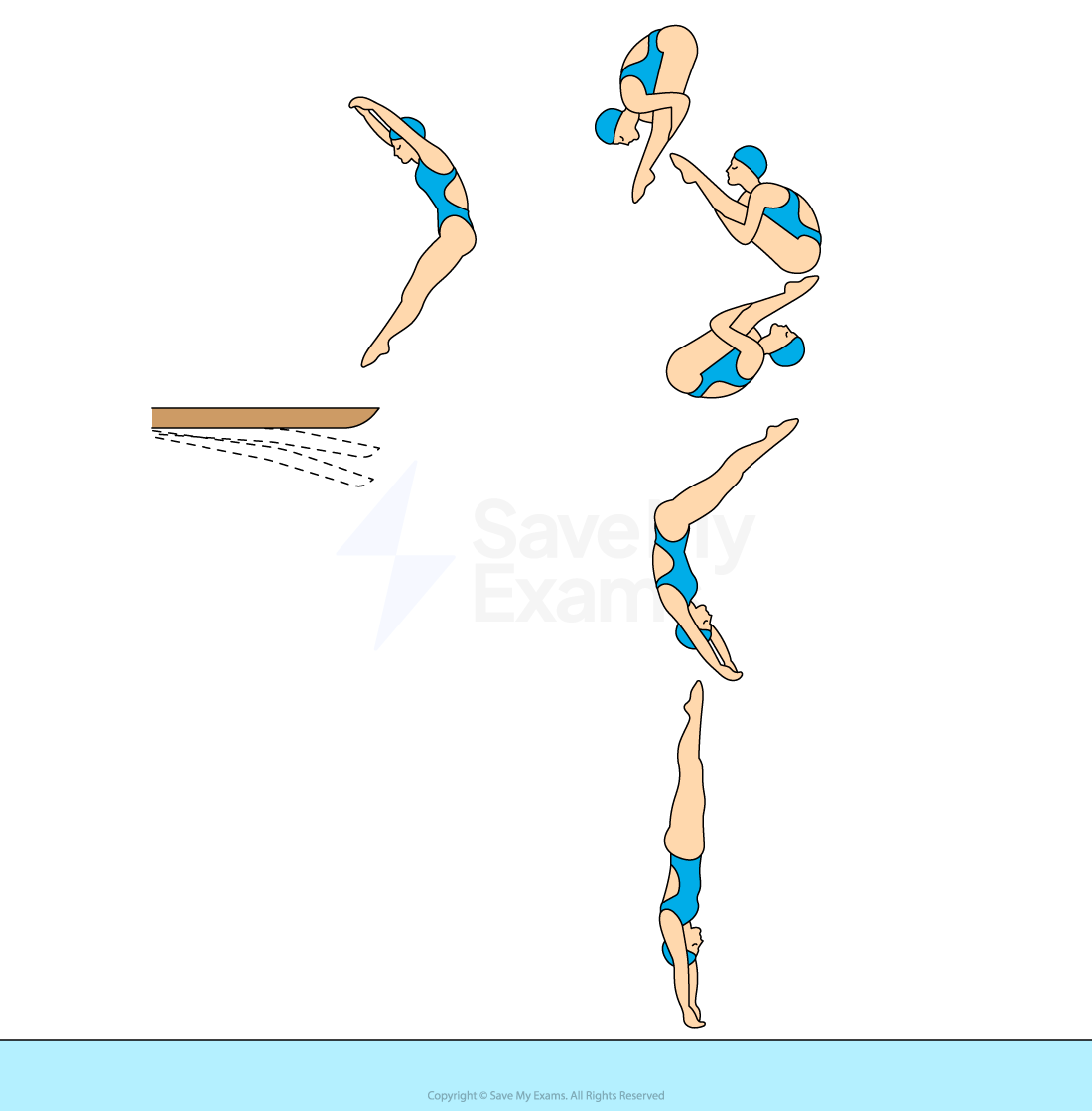
Illustration of a diver performing a dive sequence in six stages from jumping off the board to entering the water. At the top of the dive, their arms and legs are tucked in, whereas at the bottom of the dive, they are out-stretched

During their fall, the diver pulls their arms and legs into a tight tuck position while in the air and straightens them before entering the water.

Which of the following correctly describes the changes to the diver's rotational inertia and angular velocity as they bring their limbs closer to their body?

A The rotational inertia and angular velocity both increase

B The rotational inertia decreases while the angular velocity increases

C The rotational inertia increases while the angular velocity decreases

D The rotational inertia and angular velocity both decrease

The correct answer is B

Answer:

Step 1: Analyze the scenario

After the diver leaves the springboard, there is no longer a resultant torque acting on them
This means their angular momentum remains constant throughout the dive

Step 2: Eliminate the incorrect options

The conservation of angular momentum states:

$I_{i} ω_{i} = I_{f} ω_{f} = constant$

When the diver tucks their arms and legs in closer to their body, they decrease their rotational inertia
- This eliminates options A & C

Step 3: Deduce the correct option

To conserve angular momentum, when the diver's rotational inertia decreases, their angular velocity must increase
Therefore, the correct option is B

Conditions for the transfer of angular momentum

A system may be selected so that the total angular momentum of that system is constant
- The system can be defined as the objects or rigid system involved in the interaction
- The surroundings can then be defined as anything outside of the chosen system

The total angular momentum of a system can be changed only by a net external torque
When the net external torque on an object or rigid system is nonzero:
- any change to a system's angular momentum must be due to a transfer of angular momentum between the system and its surroundings
- the conservation of angular momentum principle is not valid
When the net external torque on an object or rigid system is zero (i.e. in an isolated system):
- the total angular momentum of the system is constant
- any change to the angular momentum within the system must be balanced by an equal and opposite change of angular momentum elsewhere within the system
- the conservation of angular momentum principle is valid

Transfer of angular momentum by a net external torque

A rotating system showing three particles with masses m1, m2, and m3 moving with velocities v1, v2 and v3 at different distances r1, r2, and r3 from the rotational axis. One label explains that the internal torques cancel out, so these cannot change the total angular momentum. The other label explains that only a net external torque can change the total angular momentum. — **If the net external torque on the selected system is nonzero, angular momentum is transferred between the system and the surroundings**

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Next topic

Did this page help you?