Angular Momentum (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself

Author

Katie M

Expertise

Physics

Angular momentum

Angular momentum is the rotational equivalent of linear momentum
The magnitude of the angular momentum of a rigid system about a specific axis can be described by the equation:

$L = I ω$

Where:
- $L$ = angular momentum, in $kg \cdot m^{2} / s$
- $I$ = rotational inertia, in $kg \cdot m^{2}$
- $ω$ = angular velocity, in $rad / s$

Angular Momentum of a Particle

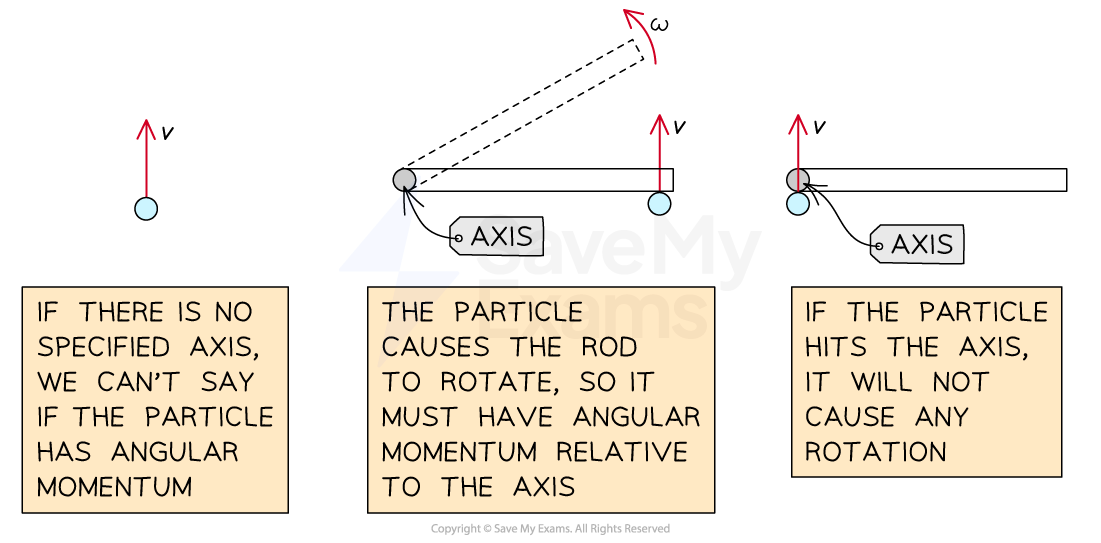
Objects traveling in a straight line can possess both linear and angular momentum
The magnitude of this angular momentum depends onthe particle's position relative to an axis of rotation
- When a particle moves on a line relative to the axis, it will cause rotation and therefore has angular momentum
- When a particle moves on a line that passes through the axis, it will not cause rotation and therefore has zero angular momentum
Therefore, an axis can be selected to change an object's angular momentum

The magnitude of an object's angular momentum depends on:
- the distance between a chosen reference point and the object
- the mass of the object
- the linear speed of the object
- the angle between the radial distance and the velocity of the object
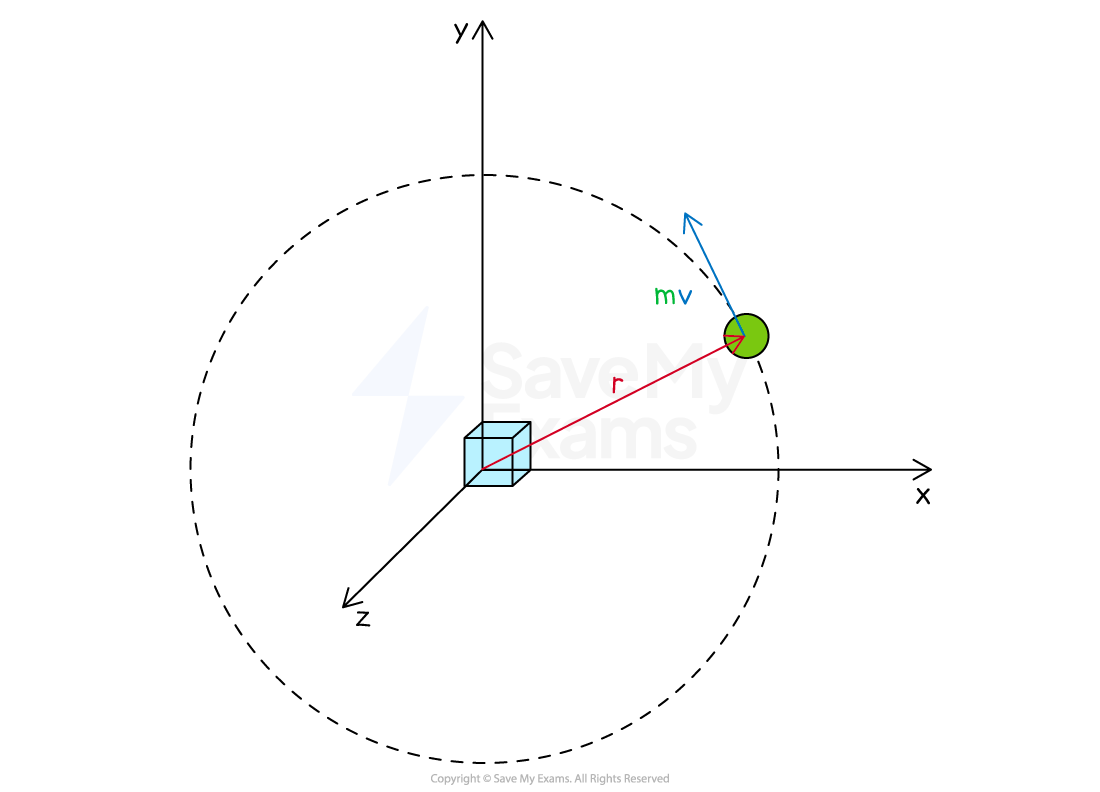
The rotational inertia of a particle at a distance $r$ from an axis of rotation is equal to:

$I = m r^{2}$

The angular velocity of the particle is given by:

$ω = \frac{v}{r}$

Therefore, the angular momentum of a particle about a given reference point is:

$L = I ω = (m r^{2}) (\frac{v}{r}) = m v r$

Where:
- $m$ = mass of the object, in $kg$
- $v$ = linear speed of the object, in $m / s$
- $r$ = distance between the reference point and the object, in $m$
This equation only applies when the axis is perpendicular to the plane of the object's motion

Angular momentum of a particle moving in a circular path

A particle of mass m moving with velocity v in a circular path. The distance between the particle and the rotational axis is r. The velocity and distance arrows are at right angles to each other. — **The angular momentum of a particle moving in a circular path is given by the product of its mass, linear velocity and distance from the rotational axis**

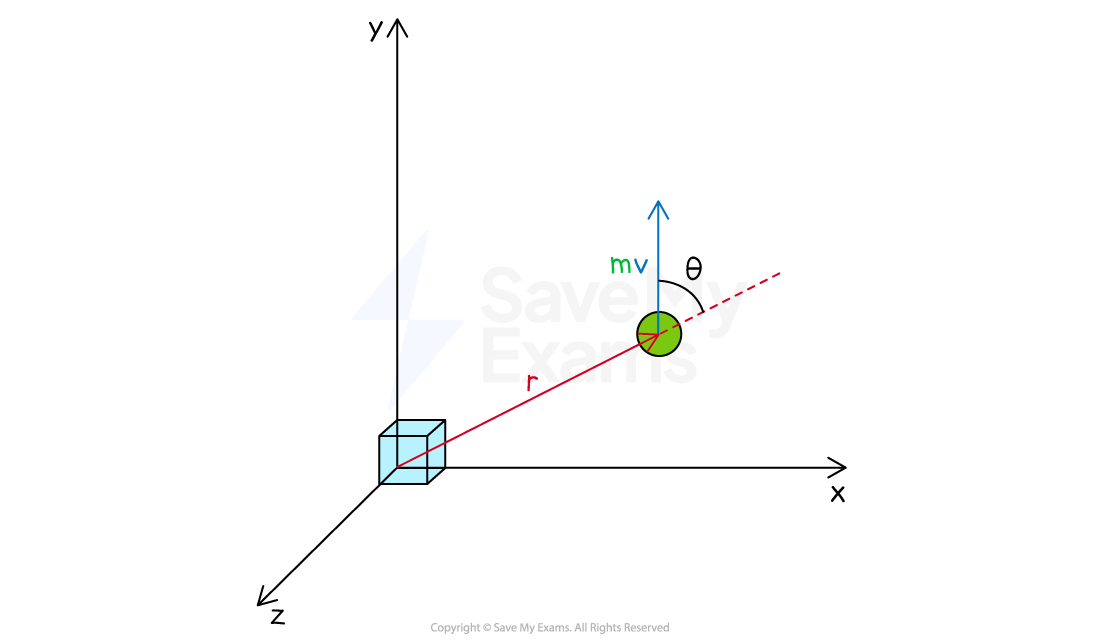
When the axis is not perpendicular, the magnitude of the angular momentum is:

$L = m v r \sin θ$

Where:
- $θ$ = the angle between the distance $r$ and the object's velocity $v$ , in $rad$

Angular momentum of a particle moving at an angle

A particle of mass m moving with velocity v in a straight line. The distance between the particle and the rotational axis is r. The velocity and distance arrows are at an angle of θ to each other. — The angular momentum of a particle moving in a straight line is given by the product of its mass, linear velocity, distance from the rotational axis and angle the angle between the radial distance and the velocity of the particle

Worked Example

A horizontal rigid bar is pivoted at its center so that it is free to rotate. A particle of mass $3 M$ is attached at one end of the bar and a container is attached at the other end, both are at a distance $R$ from the central pivot. With respect to the pivot, the rigid bar has rotational inertia $I = \frac{1}{6} M R^{2}$ .

A particle of mass $M$ moves with velocity $v$ perpendicular to the rod as shown in the diagram.

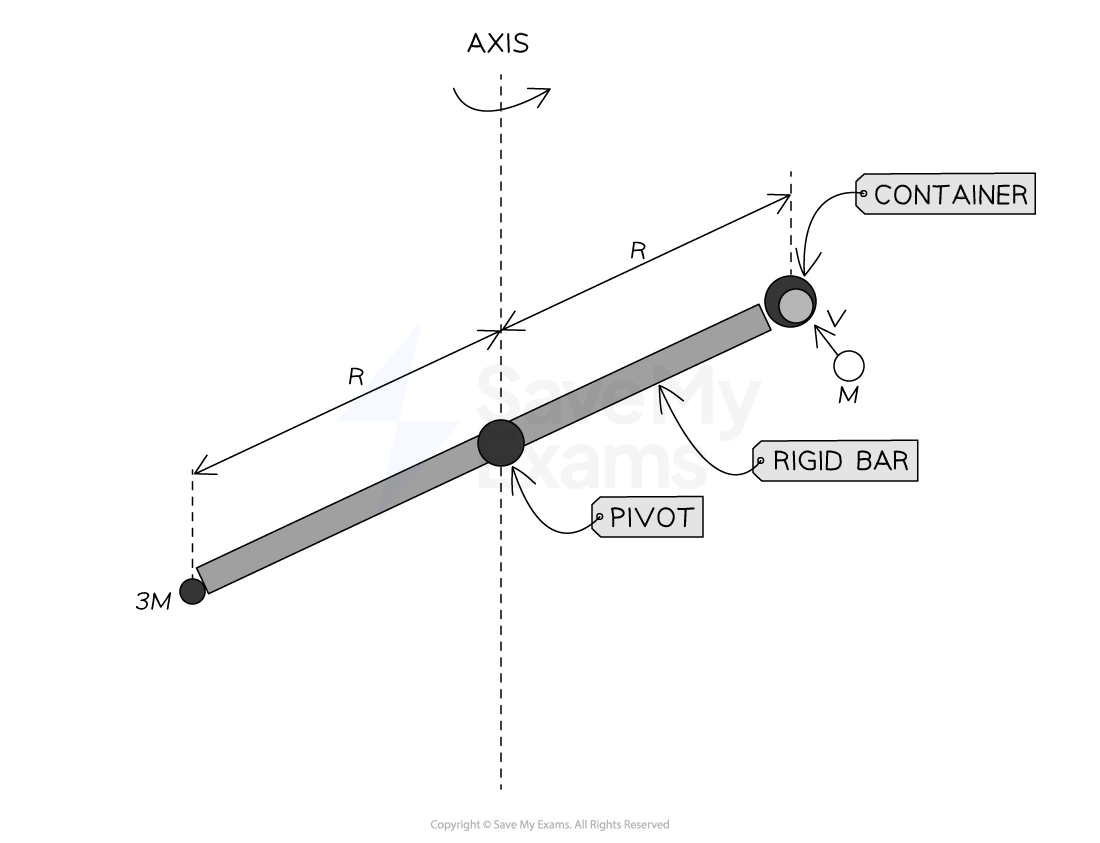
Diagram showing a rotating rigid bar with a pivot at the center and masses 3M and M at opposite ends. The mass 3M is on the left, and a container with mass M is on the right, each a distance R from the pivot.

The particle collides with the container and stays within it as the system starts to rotate about the vertical axis with angular velocity $ω$ .

Which of the following expressions correctly represents the angular momentum of the system about the vertical axis just after the collision?

A $4 M R^{2} ω$

B $4 M R v$

C $\frac{25}{6} M R^{2} ω$

D $\frac{25}{6} M R v$

The correct answer is C

Answer:

Step 1: Analyze the scenario

Before the collision:
- the rigid bar, container, and particle of mass $3 M$ are all stationary
- the particle of mass $M$ moves with linear velocity $v$

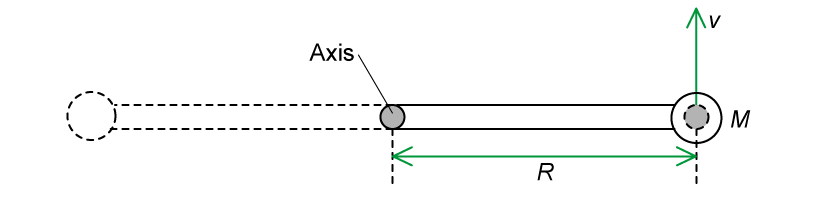
Diagram of a rigid bar with the midpoint fixed on an axis and the other end marked with mass M. Distance from the axis to M is labeled R, and velocity v is indicated as perpendicular to R.

After the collision, the whole system rotates with an angular velocity of $ω$

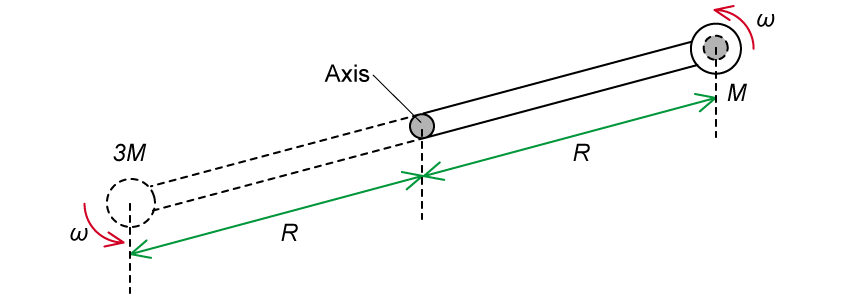
Diagram showing a rigid bar with masses 3M and M at each end, rotating around an axis in the center. Distance between each mass and the axis labeled R. Both masses rotate clockwise with angular velocity omega.

Step 2: Eliminate any incorrect answers

The total angular momentum of the system is provided by the particle of mass $M$ and is equal to $M R v$
The question asks about the angular momentum after the collision, which is also equal to $M R v$ (due to the conservation of angular momentum)
This isn't one of the options, so, the final answer must be in terms of $ω$
- This eliminates options B and D

Step 3: Determine the total rotational inertia of the system

The rotational inertia of
- the rigid bar is $I = \frac{1}{6} M R^{2}$
- the particle of mass $M$ is $I = M R^{2}$
- the particle of mass $3 M$ is $I = 3 M R^{2}$
The total rotational inertia of the system is the sum of all the rotational inertia components

$I = \sum m r^{2} = \frac{1}{6} M R^{2} + M R^{2} + 3 M R^{2}$

$I = \frac{25}{6} M R^{2}$

Step 4: Determine the angular momentum of the system

The angular momentum of the system is equal to:

$L = I ω$

The angular momentum of the system after the collision is:

$L = \frac{25}{6} M R^{2} ω$

Therefore, option C is correct

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Next topic

Did this page help you?