Angular Impulse Graphs (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself

Author

Katie M

Expertise

Physics

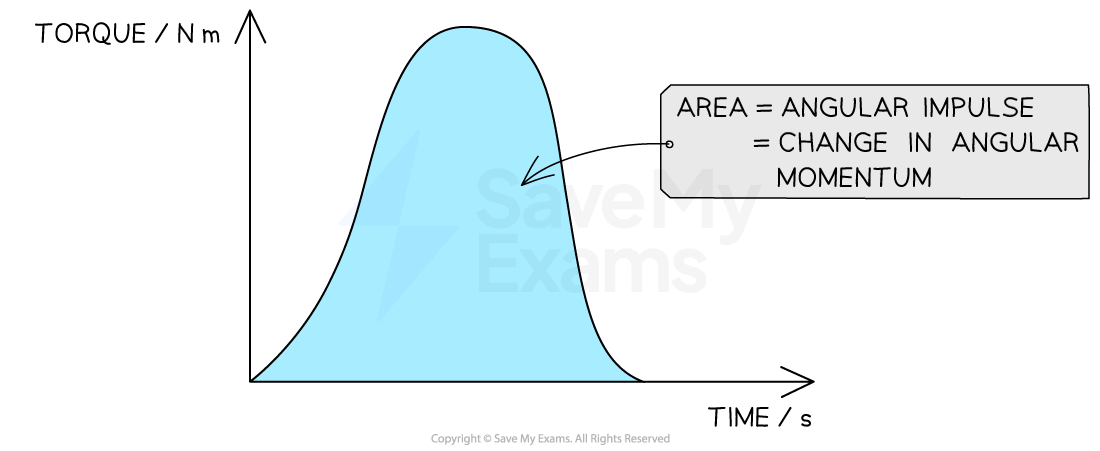
Torque-time graph

A changing torque can be plotted as a function of time
The angular impulse delivered to an object or rigid system is equal to the product of torque and time
Therefore, the area under the torque-time graph is equal to
- angular impulse
- change in angular momentum

$area = τ ∆ t = angular impulse = ∆ L$

Determining angular impulse from a torque-time graph

Graph of torque in newton meters (Nm) against time in seconds (s) with a label indicating that the area under the curve represents the angular impulse or change in angular momentum — **When the torque is not constant, the angular impulse is the area under a torque–time graph**

Worked Example

The graph shown represents the torque exerted on an object as a function of time over a 5-second interval.

Graph of torque (τ) vs. time (t) showing values in N m. Torque rises from 0 to 10 between 0 and 2 seconds, drops to 0 by 3 seconds, then stays at -5 until 5 seconds.

The object has a rotational inertia of 5.0 kg·m². At $t$ = 0 s, the object has an angular velocity of −2.0 rad/s.

Determine the angular velocity of the object at $t$ = 5 s.

Answer:

Step 1: Analyze the scenario

From $t$ = 0 to $t$ = 2 s, the torque increases to a maximum of 10 N·m, and then, from $t$ = 2 s to $t$ = 3 s, the torque decreases back to 0 N·m
At $t$ = 3 s, the direction of the applied torque changes
From $t$ = 3 to $t$ = 5 s, the torque remains at a value of −5 N·m
Overall, the angular impulse delivered to the object:
- between $t$ = 0 to $t$ = 3 s is positive, so the angular velocity will increase
- between $t$ = 3 to $t$ = 5 s is negative, so the angular velocity will decrease

Step 2: Determine the change in angular momentum over the 5 s interval

The area under a torque-time graph is equal to angular impulse, or the change in angular momentum

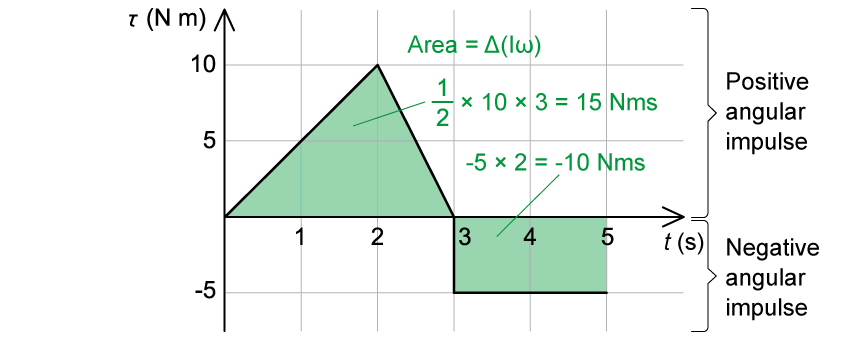
Graph depicting torque (τ) in N·m versus time (t) in seconds, showing positive and negative angular impulses. The positive impulse (0-3s) is a triangle, the negative (3-5s) is a rectangle.

Area under the positive curve (triangle) = $\frac{1}{2} \times 10 \times 3 = 15 N \cdot m \cdot s$
Area under the negative curve (rectangle) = $- 5 \times 2 = - 10 N \cdot m \cdot s$
Therefore, the angular impulse, or change in angular momentum is:

$∆ L = 15 - 10 = 5 N \cdot m \cdot s$

Step 3: Determine the final angular velocity of the object

The change in angular momentum is equal to

$∆ L = I ∆ ω = I (ω - ω_{0})$

Where $I$ = 5.0 kg·m² and $ω_{0}$ = −2.0 rad/s.
Therefore, when $t$ = 5 s, the angular velocity is:

$5 = 5.0 (ω - (- 2))$

$ω = - 1.0 rad / s$

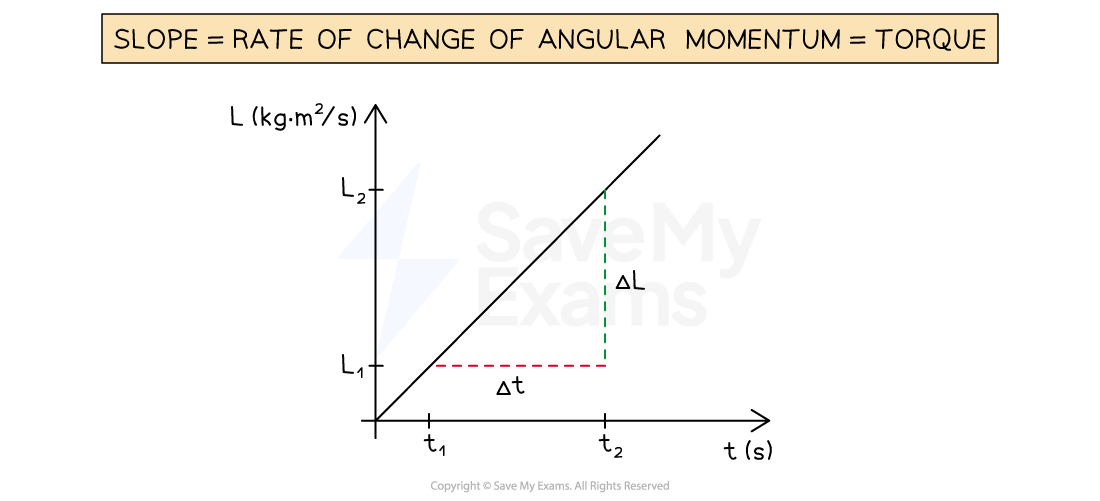
Angular momentum-time graph

A changing angular momentum can be plotted as a function of time
The net torque exerted on a system is equal to the rate of change of angular momentum
Therefore, torque is equal to the slope of an angular momentum-time graph

$slope = \frac{L_{2} - L_{1}}{t_{2} - t_{1}} = \frac{∆ L}{∆ t} = τ_{n e t}$

Determining torque from an angular momentum-time graph

Graph of angular momentum in kg·m2/s against time in s, with a label indicating that the slope represents torque — **When angular momentum varies with time, the net torque exerted on the system can be found from the slope of the angular momentum-time graph**

Worked Example

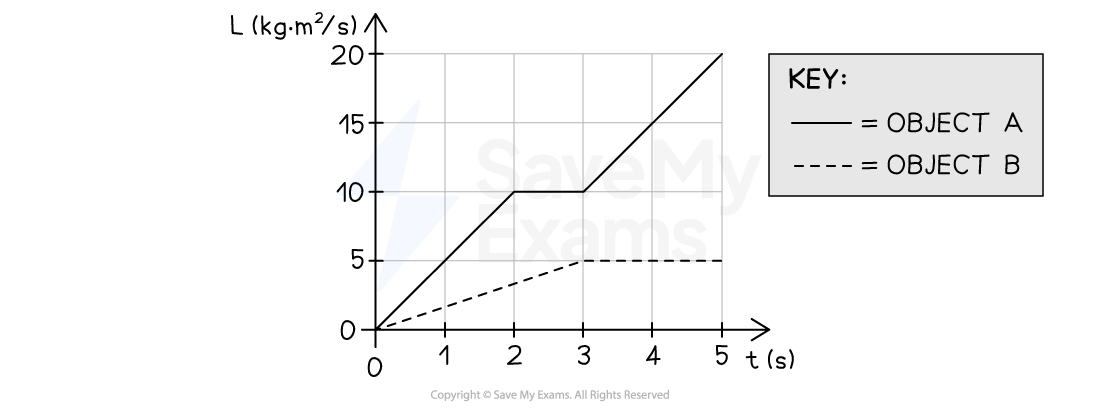
The graph shown represents the angular momentum of the two objects, A and B, as functions of time between time $t$ = 0 s and $t$ = 5 s.

The average magnitudes of the net torques on objects A and B from $t$ = 0 s to $t$ = 5 s are $τ_{A}$ and $τ_{B}$ , respectively.

Graph showing the angular momentum (L) versus time (t) for Object A (solid line) and Object B (dashed line).
Object A: between t = 0 to t = 2 s, angular momentum increases from 0 to 10 kgm2/s, between t = 2 to t = 3 s, angular momentum does not increase, between t = 3 to t = 5 s, angular momentum increases from 10 to 20 kgm2/s.
Object B: between t = 0 to t = 3 s, angular momentum increases from 0 to 5 kgm2/s, between t = 3 to t = 5 s, angular momentum does not increase.

Which of the following expressions correctly relates the magnitudes of the average torques?

A $τ_{B} = 4 τ_{A}$

B $τ_{B} = 2 τ_{A}$

C $τ_{B} = \frac{1}{2} τ_{A}$

D $τ_{B} = \frac{1}{4} τ_{A}$

The correct answer is D

Answer:

Step 1: Analyze the scenario

Object A and B experience a varying net external torque over the 5 second interval
The average magnitude of the net torque on each object is given by:

$τ_{a v g} = \frac{∆ L}{∆ t}$

Where $∆ L$ is the change in momentum from $t$ = 0 s to $t$ = 5 s

Step 2: Determine the change in angular momentum for each object

Both A and B have $L$ = 0 kg·m²/s at $t$ = 0 s
For object A:
- angular momentum: $L_{A}$ = 20 kg·m²/s at $t$ = 5 s
- change in angular momentum: $∆ L_{A}$ = 20 kg·m²/s
For object B:
- angular momentum: $L_{B}$ = 5 kg·m²/s at $t$ = 5 s
- change in angular momentum: $Δ L_{B}$ = 5 kg·m²/s

Step 3: Determine the average torque on each object

The average torque on object A is:

$τ_{A} = \frac{20}{5} = 4 N \cdot m$

The average torque on object B is

$τ_{B} = \frac{5}{5} = 1 N \cdot m$

Step 4: Determine the ratio of the average torques

The ratio of the average torque on object B to object A is

$\frac{τ_{B}}{τ_{A}} = \frac{1}{4}$

$τ_{B} = \frac{1}{4} τ_{A}$

Therefore, the correct option is D

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Next topic

Did this page help you?

Angular Impulse Graphs (College Board AP® Physics 1: Algebra-Based)

Study Guide

Torque-time graph

Determining angular impulse from a torque-time graph

Worked Example

Angular momentum-time graph

Determining torque from an angular momentum-time graph

Worked Example

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Katie M