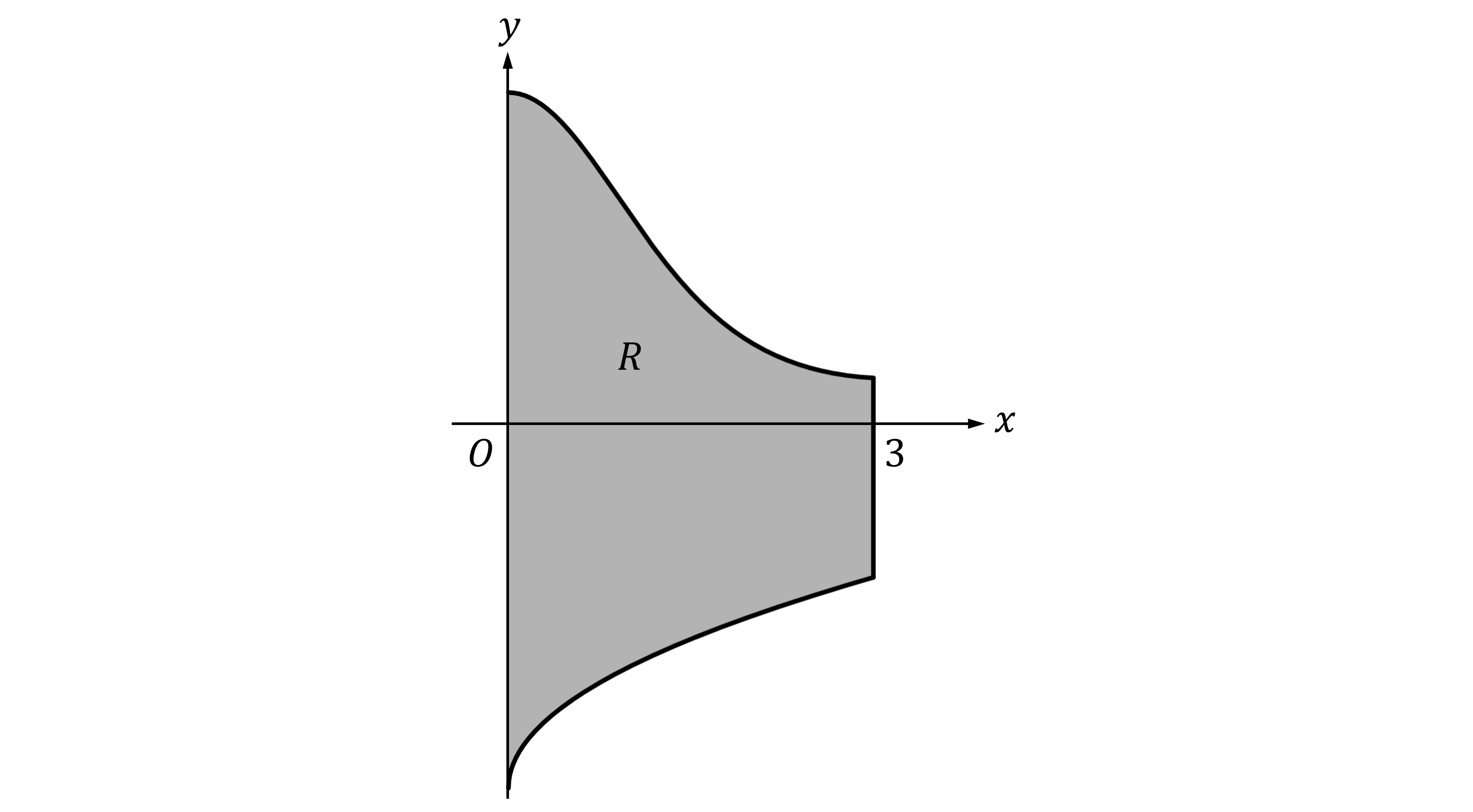
Let be the region enclosed by the graphs of
and
, the
-axis, and the vertical line
, as shown in the figure above.
Region is the base of a solid. For the solid, at each
the cross section perpendicular to the
-axis has area
. Find the volume of the solid.
Did this page help you?









