Derivatives of Polar Curves (College Board AP® Calculus BC): Study Guide

Written by: Mark Curtis

Reviewed by: Dan Finlay

Updated on 19 February 2025

Derivatives of polar curves

How do I find dr/dθ of a polar curve?

To find $\frac{d r}{d θ}$ of a polar curve, $r (θ)$ , differentiate it with respect to $θ$
- e.g. if $r = 1 + \cos θ$ then $\frac{d r}{d θ} = - \sin θ$
The sign of the derivative can be interpreted as follows:
- $\frac{d r}{d θ} > 0$ means $r$ is increasing with respect to $θ$
  - Points on the curve are moving further away from the origin as $θ$ increases
- $\frac{d r}{d θ} < 0$ means $r$ is decreasing with respect to $θ$
  - Points on the curve are moving closer to the origin as $θ$ increases
For certain polar curves, the point at which $\frac{d r}{d θ} = 0$ is the point that has the greatest distance from the origin
If two polar curves are given, $r_{1} (θ)$ and $r_{2} (θ)$ , then
- $\frac{d}{d θ} (r_{1} - r_{2})$ is the rate at which the distance between the two curves is changing with respect to $θ$

How do I find dx/dθ of a polar curve?

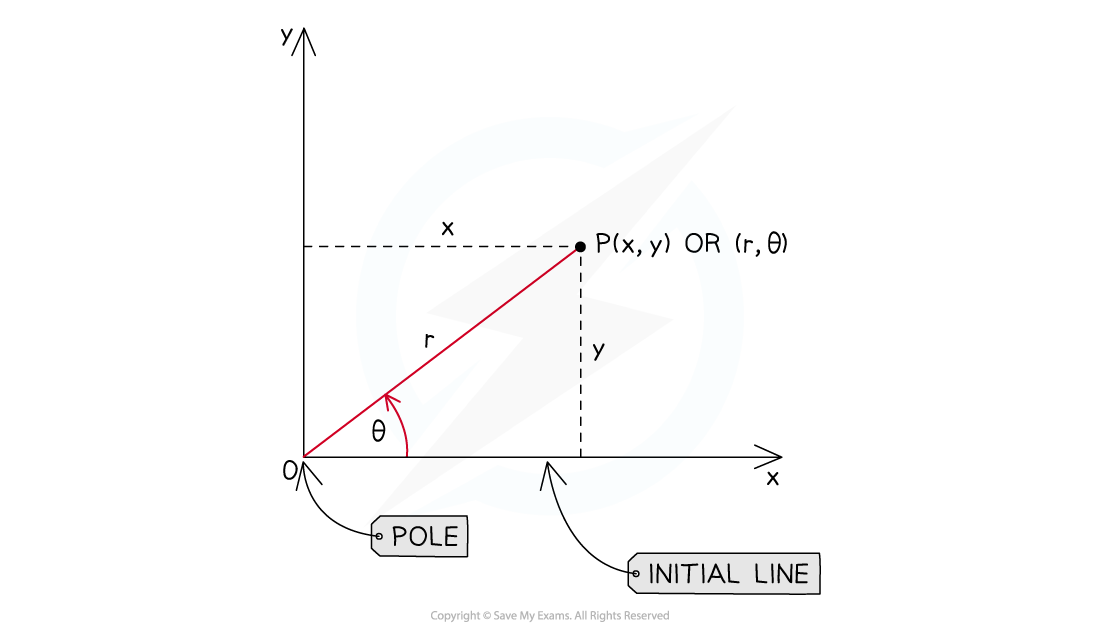
Diagram of polar coordinates with a point P(x, y) or (r, θ). The angle θ and radius r are marked from the origin, labelled as "Pole" with the x-axis as "Initial Line".

To find $\frac{d x}{d θ}$ of a polar curve, $r (θ)$ , first differentiate the trigonometric relationship $x = r \cos θ$ using implicit differentiation (as $r$ is not a constant - it varies with $θ$ ) and the product rule
- $\frac{d x}{d θ} = \frac{d r}{d θ} \cos θ - r \sin θ$
- Then substitute in $r (θ)$ and $\frac{d r}{d θ}$
The sign of the derivative can be interpreted as follows:
- $\frac{d x}{d θ} > 0$ means the $x$ -coordinate is increasing with respect to $θ$
  - Points on the curve are moving in the positive $x$ -direction as $θ$ increases
- $\frac{d x}{d θ} < 0$ means the $x$ -coordinate is decreasing with respect to $θ$
  - Points on the curve are moving in the negative $x$ -direction as $θ$ increases

How do I find dy/dθ of a polar curve?

To find $\frac{d y}{d θ}$ of a polar curve, $r (θ)$ , first differentiate the trigonometric relationship $y = r \sin θ$ using the product rule (as $r$ is not a constant - it varies with $θ$ )
- $\frac{d y}{d θ} = \frac{d r}{d θ} \sin θ + r \cos θ$
- Then substitute in $r (θ)$ and $\frac{d r}{d θ}$
The sign of the derivative can be interpreted as follows:
- $\frac{d y}{d θ} > 0$ means the $y$ -coordinate is increasing with respect to $θ$
  - Points on the curve are moving upwards as $θ$ increases
- $\frac{d y}{d θ} < 0$ means the $y$ -coordinate is decreasing with respect to $θ$
  - Points on the curve are moving downwards as $θ$ increases

Examiner Tips and Tricks

In an exam question, it is often easier to derive the formulas for $\frac{d x}{d θ}$ and $\frac{d y}{d θ}$ using the product rule, than trying to learn their results.

How do I find the slope of a polar curve, dy/dx?

The formula for the slope of a polar curve, $\frac{d y}{d x}$ , is

$\frac{d y}{d x} = \frac{\frac{d y}{d θ}}{\frac{d x}{d θ}} = \frac{\frac{d r}{d θ} \sin θ + r \cos θ}{\frac{d r}{d θ} \cos θ - r \sin θ}$

The derivatives $\frac{d y}{d θ}$ and $\frac{d x}{d θ}$ come from above
The formula itself comes from the chain rule:
- $\frac{d y}{d x} = \frac{d y}{d θ} \cdot \frac{d θ}{d x} = \frac{d y}{d θ} \cdot \frac{1}{\frac{d x}{d θ}}$

Examiner Tips and Tricks

Questions may ask you to find the equation of a tangent to a polar curve, which will require you to calculate the slope.

How do I find the second derivative of a polar curve with respect to x?

The formula for the second derivative of $y$ with respect to $x$ , $\frac{d^{2} y}{d x^{2}}$ , for polar equations in terms of $θ$ is

$\frac{d^{2} y}{d x^{2}} = \frac{\frac{d}{d θ} (\frac{d y}{d x})}{\frac{d x}{d θ}}$

$\frac{d}{d θ} (\frac{d y}{d x})$ means differentiate the expression for the slope of the polar curve, $\frac{d y}{d x}$ , with respect to $θ$
- Recall that $\frac{d y}{d x} = \frac{\frac{d y}{d θ}}{\frac{d x}{d θ}} = \frac{\frac{d r}{d θ} \sin θ + r \cos θ}{\frac{d r}{d θ} \cos θ - r \sin θ}$
- and that $\frac{d x}{d θ} = \frac{d r}{d θ} \cos θ - r \sin θ$ from above
The formula for the second derivative comes from the chain rule:
- $\frac{d^{2} y}{d x^{2}} = \frac{d}{d x} (\frac{d y}{d x}) = \frac{d}{d θ} (\frac{d y}{d x}) \cdot \frac{d θ}{d x} = \frac{d}{d θ} (\frac{d y}{d x}) \cdot \frac{1}{\frac{d x}{d θ}}$

Examiner Tips and Tricks

If you have studied parametric equations, then it helps to know that the second derivative formula of a polar curve is the same as the second derivative formula of a parametric curve, just with $θ$ instead of $t$ .

How do I find derivatives of polar curves with respect to time, t?

To find derivatives of a polar curve with respect to time, $t \geq 0$ , use the chain rule (related rates of change)
- These are used in questions about a particle moving around a polar curve
For example, if $\frac{d r}{d t} = 2$ at $θ = \frac{π}{2}$ on the curve $r = 10 \cos θ$ , then to find $\frac{d θ}{d t}$ at $θ = \frac{π}{2}$ :
- Use that $\frac{d θ}{d t} = \frac{d θ}{d r} \cdot \frac{d r}{d t}$
  - Substitute in $θ = \frac{π}{2}$ and $\frac{d r}{d t} = 2$
  - Use that $\frac{d θ}{d r} = \frac{1}{\frac{d r}{d θ}}$ where $\frac{d r}{d θ} = - 10 \sin θ$ (by differentiating $r = 10 \cos θ$ )
- This gives $\frac{1}{- 10 \sin (\frac{π}{2})} \cdot 2 = - \frac{1}{5}$
If you are given a relationship between $θ$ and $t$ , you can substitute this into the equation of the polar curve
- e.g. If $r = 10 \cos θ$ and $θ = t^{3}$ , then $r = 10 \cos (t^{3})$
- The position vector is then given by $<x, y> = <r \cos θ, r \sin θ> = <10 \cos^{2} (t^{3}), 10 \cos (t^{3}) \sin (t^{3})>$
  - See the study guide on 'Motion with Vector-Valued Functions'

Examiner Tips and Tricks

If a polar coordinates question asks to find a derivative at a particular point, read the question carefully to see which derivative is being asked for ('with respect to' what).

Worked Example

A sketch of the polar curve $r = e^{- θ}$ is shown below, where $0 \leq θ \leq π$ .

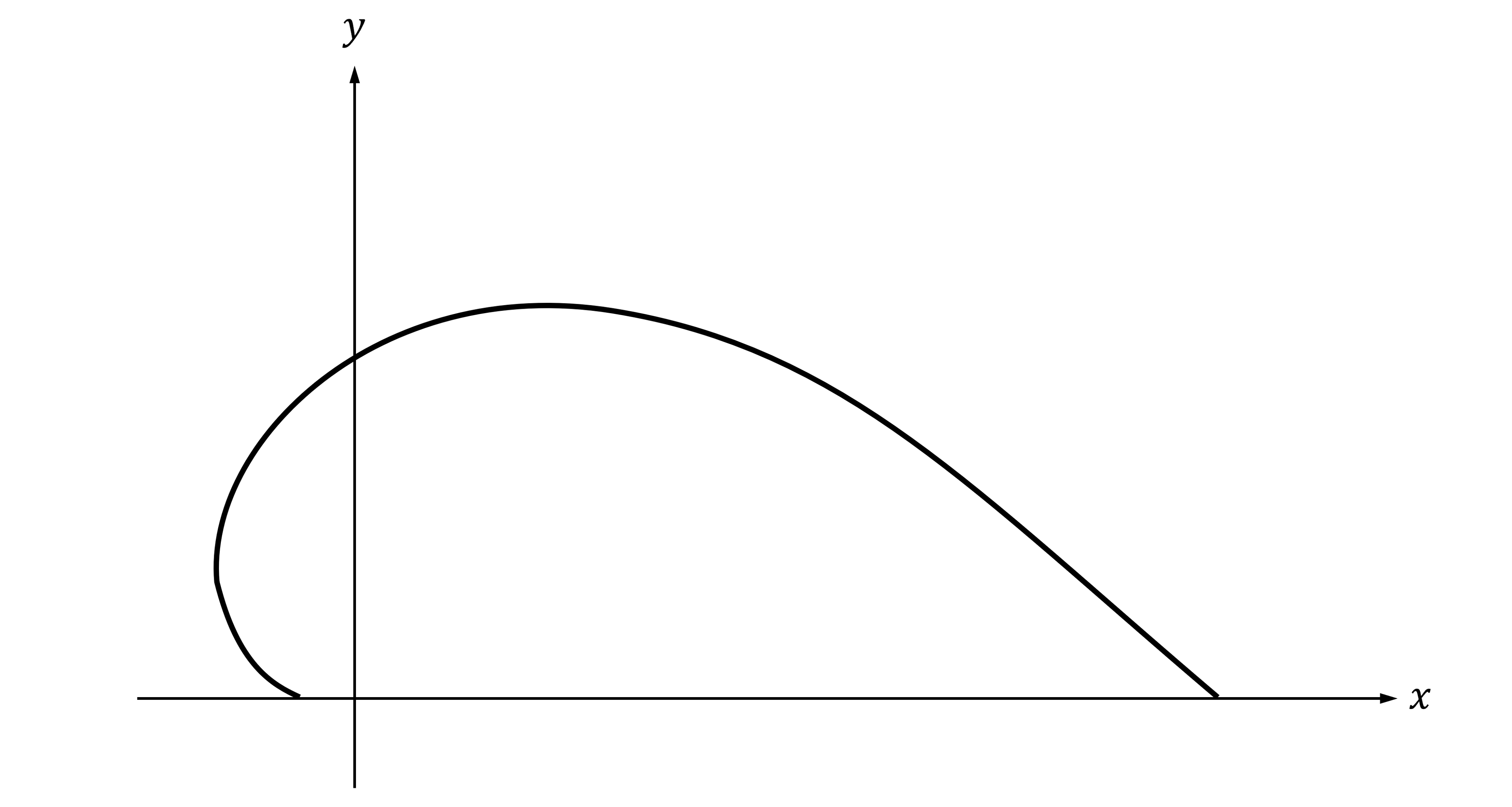
Graph of the polar equation r = e^(-theta), curving into the origin anticlockwise, intersecting the x-axis.

(a) Find $\frac{d r}{d θ}$ at $θ = 0$ and interpret the result.

Differentiate $r = e^{- θ}$ with respect to $θ$

$\frac{d r}{d θ} = - e^{- θ}$

Substitute in $θ = 0$

$\frac{d r}{d θ} = - e^{- 0} = - 1$

A negative value of $\frac{d r}{d θ}$ means points on the curve are moving closer to the origin

$\frac{d r}{d θ} = - 1$ at $θ = 0$ which means $r$ is decreasing with respect to $θ$ , so the points on the curve are moving closer to the origin as $θ$ increases

(b) Find the slope of the line tangent to the curve at $θ = \frac{π}{4}$ .

The formula for the slope of a polar curve is $\frac{d y}{d x} = \frac{\frac{d y}{d θ}}{\frac{d x}{d θ}} = \frac{\frac{d r}{d θ} \sin θ + r \cos θ}{\frac{d r}{d θ} \cos θ - r \sin θ}$

Substitute $r = e^{- θ}$ and $\frac{d r}{d θ} = - e^{- θ}$ into the formula and simplify

$\begin{array}{rcl} \frac{d y}{d x} & = & \frac{\frac{d y}{d θ}}{\frac{d x}{d θ}} = \frac{\frac{d r}{d θ} \sin θ + r \cos θ}{\frac{d r}{d θ} \cos θ - r \sin θ} \\ = & \frac{- e^{- θ} \sin θ + e^{- θ} \cos θ}{- e^{- θ} \cos θ - e^{- θ} \sin θ} \\ = & \frac{- e^{- θ} (\sin θ - \cos θ)}{- e^{- θ} (\cos θ + \sin θ)} \\ = & \frac{\sin θ - \cos θ}{\cos θ + \sin θ} \end{array}$

Now substitute $θ = \frac{π}{4}$ into the expression above

$\begin{array}{rcl} \frac{d y}{d x} & = & \frac{\sin \frac{π}{4} - \cos \frac{π}{4}}{\cos \frac{π}{4} + \sin \frac{π}{4}} \\ = & \frac{\frac{\sqrt{2}}{2} - \frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2}} \\ = & 0 \end{array}$

$\frac{d y}{d x} = 0$ at $θ = \frac{π}{4}$

(c) It is known that the derivative $\frac{d}{d θ} (\frac{d y}{d x})$ simplifies to $\frac{2}{{(\cos θ + \sin θ)}^{2}}$ . Find the value of $\frac{d^{2} y}{d x^{2}}$ at $θ = π$ .

The second derivative with respect to $x$ is given by the formula $\frac{d^{2} y}{d x^{2}} = \frac{\frac{d}{d θ} (\frac{d y}{d x})}{\frac{d x}{d θ}}$

The numerator is given in the question, $\frac{2}{{(\cos θ + \sin θ)}^{2}}$ , so substitute $θ = π$ in and simplify

$\frac{2}{{(\cos π + \sin π)}^{2}} = \frac{2}{{(- 1 + 0)}^{2}} = 2$

The denominator is $\frac{d x}{d θ} = \frac{d r}{d θ} \cos θ - r \sin θ$ which, from part (b), is $\begin{array}{rcl} - e^{- θ} \cos θ - e^{- θ} \sin θ \end{array}$

Substitute $θ = π$ in and simplify

$\begin{array}{rcl} - e^{- π} \cos π - e^{- π} \sin π & = & - e^{- π} (- 1) - e^{- π} (0) \\ = & e^{- π} \end{array}$

Divide the numerator by the denominator and simplify

$\frac{2}{e^{- π}} = 2 e^{π}$

$\frac{d^{2} y}{d x^{2}} = 2 e^{π}$ at $θ = π$

(d) A particle is moving around the curve such that at the point $θ = \frac{π}{2}$ the rate at which the angle is increasing with respect to time, $t \geq 0$ , is 3 radians per second. Find and interpret the value of $\frac{d y}{d t}$ at the point $θ = \frac{π}{2}$ .

The rate at which the angle is increasing with respect to time, $t \geq 0$ , is $\frac{d θ}{d t}$ , so

$\frac{d θ}{d t} = 3$ at $θ = \frac{π}{2}$

Use the chain rule (connected rates of change) to write $\frac{d y}{d t}$ as a derivative involving $\frac{d θ}{d t}$

$\frac{d y}{d t} = \frac{d y}{d θ} \cdot \frac{d θ}{d t}$

Find an expression for $\frac{d y}{d θ}$ , which has the formula $\frac{d y}{d θ} = \frac{d r}{d θ} \sin θ + r \cos θ$ and which has already been found in part (b)

$\begin{array}{rcl} \frac{d y}{d θ} \end{array} = \begin{array}{rcl} - \end{array} \begin{array}{rcl} e \end{array} \begin{array}{rcl} ^{- θ} \end{array} \begin{array}{rcl} \sin \end{array} \begin{array}{rcl} \end{array} \begin{array}{rcl} θ \end{array} \begin{array}{rcl} + \end{array} \begin{array}{rcl} e \end{array} \begin{array}{rcl} ^{- θ} \end{array} \begin{array}{rcl} \cos \end{array} \begin{array}{rcl} \end{array} \begin{array}{rcl} θ \end{array}$

Substitute $\frac{d y}{d θ}$ , $θ = \frac{π}{2}$ and $\frac{d θ}{d t} = 3$ into $\frac{d y}{d t} = \frac{d y}{d θ} \cdot \frac{d θ}{d t}$

$\frac{d y}{d t} = \frac{d y}{d θ} \cdot \frac{d θ}{d t} = (\begin{array}{rcl} - e^{- \frac{π}{2}} \sin \frac{π}{2} + e^{- \frac{π}{2}} \cos \frac{π}{2} \end{array}) \cdot 3 = \begin{array}{rcl} e \end{array} \begin{array}{rcl} ^{- \frac{π}{2}} \end{array} (\begin{array}{rcl} - 1 + 0 \end{array}) \cdot 3 = \begin{array}{rcl} - 3 \end{array} \begin{array}{rcl} e^{- \frac{π}{2}} \end{array}$

$\begin{array}{rcl} - 3 e^{- \frac{π}{2}} & < & 0 \end{array}$ , and a negative value of $\frac{d y}{d t}$ means the $y$ -coordinate of the particle's motion is decreasing as time increases

$\frac{d y}{d t} = - 3 e^{- \frac{π}{2}}$ at $θ = \frac{π}{2}$ , so the the $y$ -coordinate of the particle's motion is decreasing as time increases

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself

Did this page help you?

Previous:Defining Polar CoordinatesNext:Areas from a Single Polar Curve

Derivatives of Polar Curves (College Board AP® Calculus BC): Study Guide

Derivatives of polar curves

How do I find dr/dθ of a polar curve?

How do I find dx/dθ of a polar curve?

How do I find dy/dθ of a polar curve?

How do I find the slope of a polar curve, dy/dx?

How do I find the second derivative of a polar curve with respect to x?

How do I find derivatives of polar curves with respect to time, t?

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

Unit 1: Limits & Continuity

Limits

Definition of a Limit

Infinite Limits & Limits at Infinity

Properties of Limits

Evaluating Limits Analytically

Evaluating Limits Numerically & Graphically

Squeeze Theorem & Trigonometric Limits

Summary of Limits

Selecting Procedures for Determining Limits

Continuity

Continuity

Removable Discontinuities

Non-removable Discontinuities

Intermediate Value Theorem

Unit 2: Differentiation Definition & Fundamental Properties

Definition of Differentiation

Average Rate of Change

Instantaneous Rate of Change

Derivatives & Tangents

Estimating the Derivative at a Point

Differentiability & Continuity

Fundamental Properties of Differentiation

Derivative Rules

Derivatives of Exponentials and Logarithms

Derivatives of Sine and Cosine Functions

The Product Rule

The Quotient Rule

Derivatives of Tangent and Reciprocal Trig Functions

Unit 3: Differentiation of Composite, Implicit & Inverse Functions

Differentiation of Composite & Inverse Functions

The Chain Rule

The Inverse Function Theorem

Derivatives of Inverse Trigonometric Functions

Higher-Order Derivatives

Summary of Differentiation

Selecting Procedures for Calculating Derivatives

Unit 4: Contextual Applications of Differentiation

Rates of Change & Related Rates

Meaning of a Derivative in Context

Motion in a Straight Line

Related Rates

Linearization

Approximating Values of a Function

L'Hospital's Rule

L'Hospital's Rule

Unit 5: Analytical Applications of Differentiation

Graphs of Functions & Their Derivatives

Mean Value Theorem

Extreme Value Theorem

Critical Points

Increasing & Decreasing Functions

First Derivative Test for Local Extrema

Candidates Test for Global Extrema

Concavity of Functions

Second Derivative Test for Local Extrema

Graphs of f, f' & f''

Optimization Problems

Behaviors of Implicit Relations

Second Derivatives of Implicit Functions

Critical Points of Implicit Relations

Unit 6: Integration & Accumulation of Change

Integration & Antiderivatives

Indefinite Integrals

Derivatives & Antiderivatives

Indefinite Integral Rules

Constant of Integration

Riemann Sums & Definite Integrals

Accumulation of Change

Riemann Sums