Defining Polar Coordinates (College Board AP® Calculus BC): Study Guide
Defining polar coordinates
What are polar coordinates?
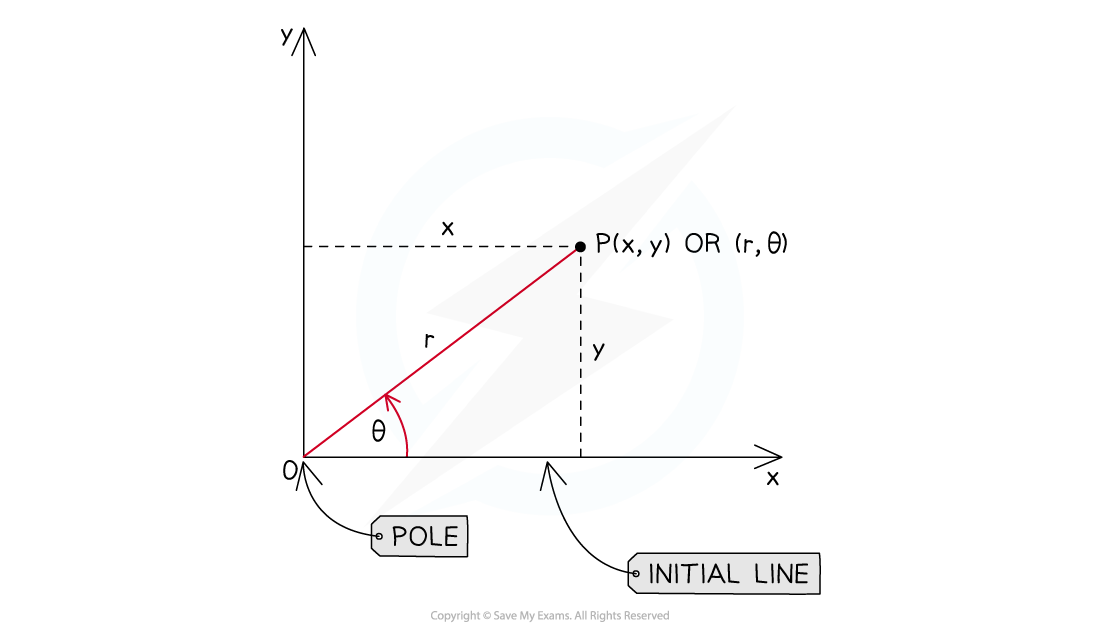
Polar coordinates are an alternative way to describe the position of points and curves in two-dimensions using
a distance,
where
can be positive or negative
measured from an origin, called a pole
and an angle,
measured in radians from an initial line (extending from the pole)
The initial line is usually the
-axis
The polar coordinates of a point are written as
These are not to be confused with a point given in
form
Negative values of
are drawn in the opposite direction to
Examiner Tips and Tricks
It will be clear in the question whether polar coordinates or and
coordinates are being used.
How are polar coordinates related to x and y coordinates?
If a point P has polar coordinates
, then the
and
coordinates in the
-plane are found by trigonometry:
It can also be helpful to make
and
the subject to give two more relationships:
These are found using trigonometric identities:
and
How do I sketch a polar curve?
A polar curve is a curve given in the form
They are sometimes given in the form
The polar curve may be restricted to a range of
values, e.g.
To sketch a polar curve, use the graph sketching function on your calculator
Change the type of graph to 'polar'
An alternative way to sketch is by plotting points
Find the distance
for some key angles,
Plot these points on a polar grid (see below)

The following are some examples of polar curves (you do not need to learn these):
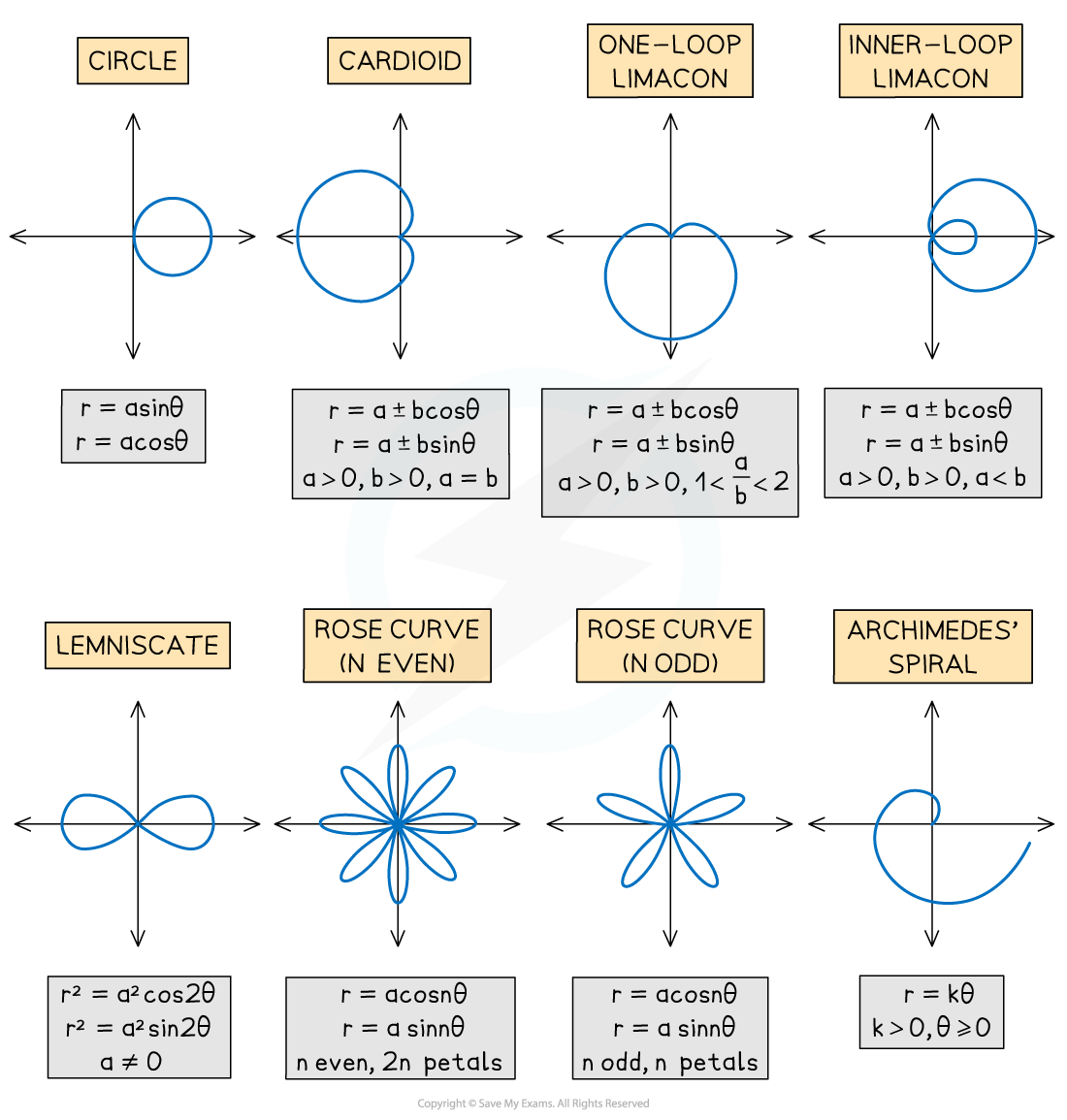
Note that the spiral
has an angle
that can continue beyond
How do I find x and y coordinates on a polar curve?
To find the
and
coordinates of a point on a polar curve, substitute the equation of the polar curve,
, into the trigonometric relationships
and
to get:
Different values of
will give different
and
coordinates
Examiner Tips and Tricks
The two relationships and
are used a lot in harder polar questions.
How do I find the average distance from the origin to a point on a polar curve?
The average distance from the origin to a point on a polar curve,
, where
is:
How do I convert a polar equation into (and out of) x and y coordinates?
To convert an equation from polar coordinates into
and
coordinates, use the algebraic relationships above
e.g.
Multiply both sides by
to get
Use that
and that
to give
By completing the square, this is
which is a circle, radius 2, centre
Note that
means
Only use the negative square root for parts of the curve where
goes negative
To convert an equation from
and
into polar coordinates, simply substitute in
and
and rearrange
You need to be able to recognize the following key examples:
| Converting | Polar equation |
|---|---|---|
(horizontal line) | ||
(vertical line) | ||
(circle, centre O, radius |
Worked Example
The polar curve is shown below, where
. The point
is on the curve at an angle of
.
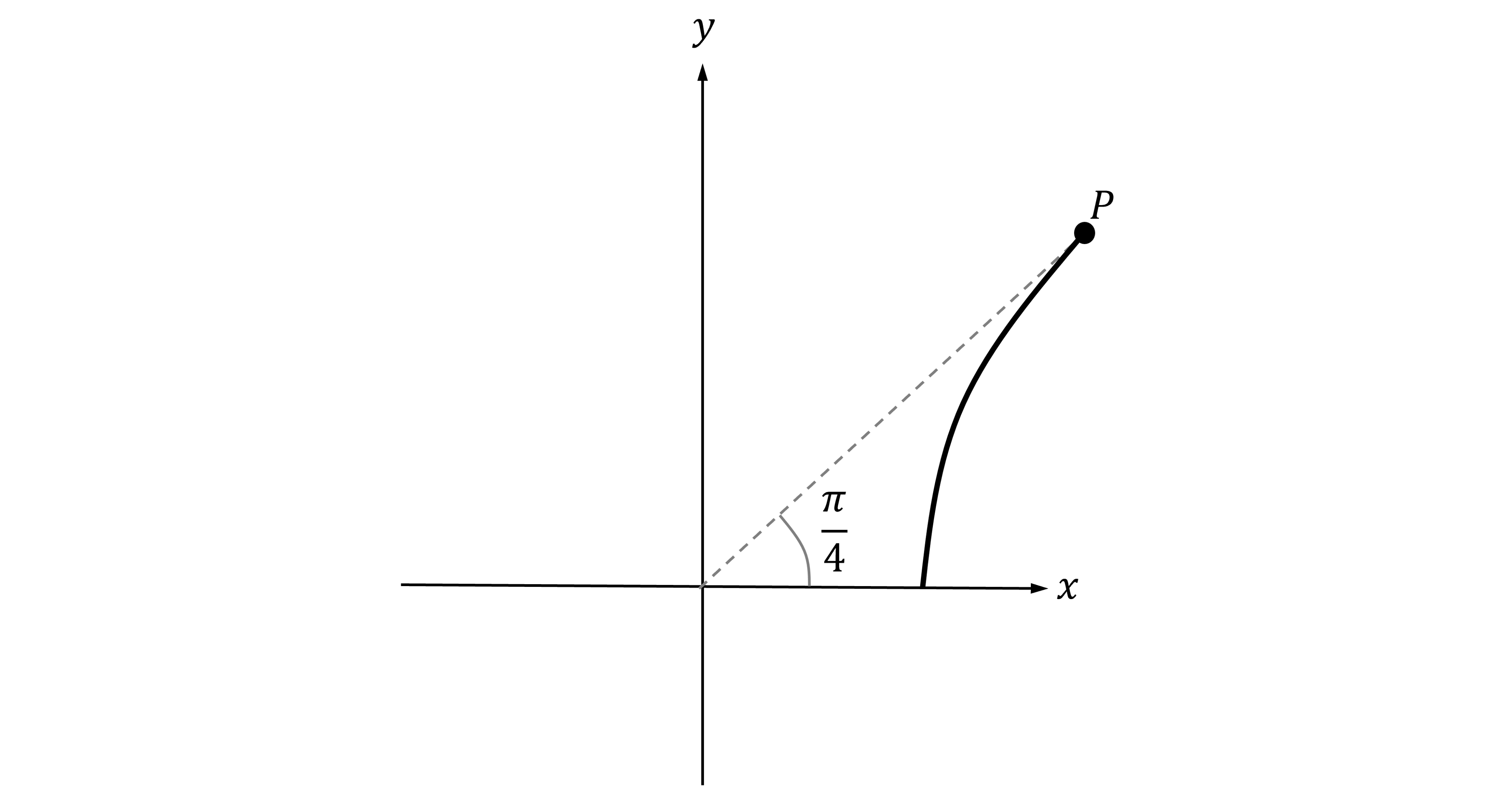
(a) Find the value of at the point
.
Answer:
Substitute into the equation
to find
and simplify
(b) Find the value of for which the
-coordinate of the curve is equal to
.
Answer:
The -coordinate of a polar curve is given by
First, substitute in
Next, substitute in the polar curve for
, simplifying the left-hand side
Solve the resulting equation to find
(c) Find the average distance from the origin to a point on the curve.
Answer:
The average distance from the origin is given by the formula
Substitute ,
and
into the formula and integrate
(d) Find the equation of the curve in terms of and
. Give your answer in the form
.
Answer:
One way is to start by multiplying both sides of the polar curve by
The left-hand side is almost the square of , so multiply both sides by
Now substitute into the left-hand side and
into the right-hand side, to give an equation just in
and
The question wants the answer in the form so make
the subject
To decide which sign to choose, first look at the sketch of the curve given in the question
The curve is in the first quadrant, meaning , so chose the positive square root

Unlock more, it's free!
Did this page help you?