Study GuidesExam QuestionsPast Papers
AP®MathsCollege BoardCalculus BCStudy GuidesUnit 9: Parametric Equations, Vector-Valued Functions & Polar CoordinatesPolar CoordinatesAreas from a Single Polar Curve

Areas from a Single Polar Curve (College Board AP® Calculus BC) : Study Guide

Mark Curtis

Written by: Mark Curtis

Reviewed by: Dan Finlay

Updated on

Areas from a single polar curve

How do I find the area enclosed by a polar curve?

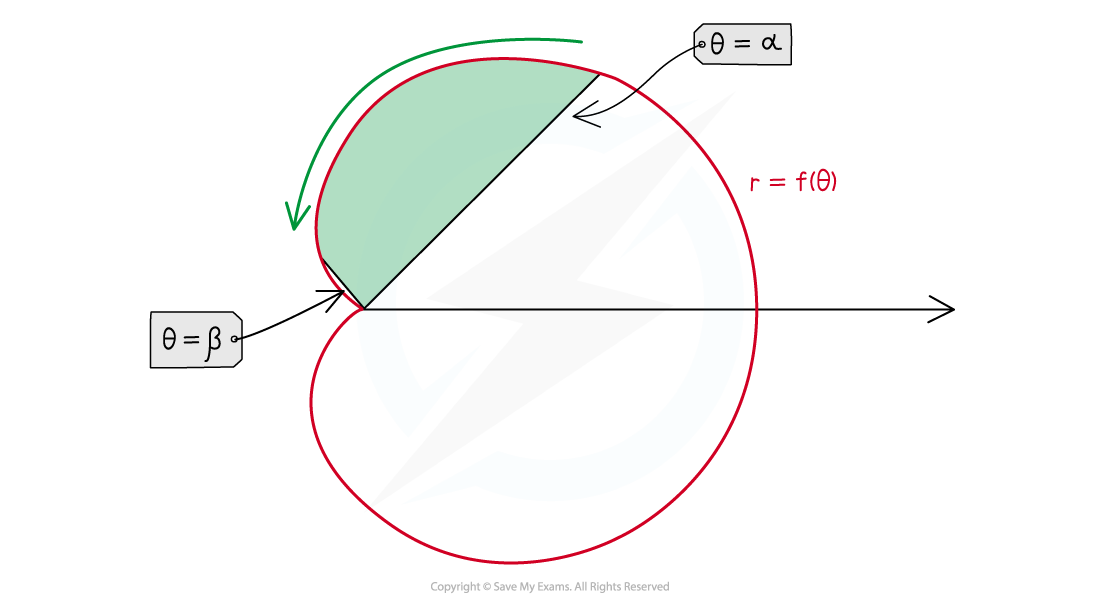
Polar graph with a shaded sector between angles alpha and beta. The curve is defined by r = f(θ) and arrows indicate direction.

  • The area, A, bounded by a polar curve, r equals f open parentheses theta close parentheses and the straight lines theta equals alpha and theta equals beta is

A equals integral subscript alpha superscript beta 1 half r squared space d theta

  • The lines theta equals alpha and theta equals beta are called rays

    • They extend from the origin (pole)

    • The area is swept out anticlockwise between them

  • The formula A equals integral subscript alpha superscript beta 1 half r squared space d theta still works for parts of the curve with negative values of r

    • This is because r gets squared in the formula

Examiner Tips and Tricks

Look out for any symmetry, as it may be possible to express larger polar areas as multiples of smaller polar areas.

Examiner Tips and Tricks

In the non-calculator sections of the exam, you are often asked to leave polar areas as definite integrals. In the calculator sections, you are expected to use your calculator to evaluate these definite integrals.

Worked Example

The polar curve r equals sin space 3 theta is shown below, where 0 less or equal than theta less or equal than pi. Part of the total area enclosed has been shaded.

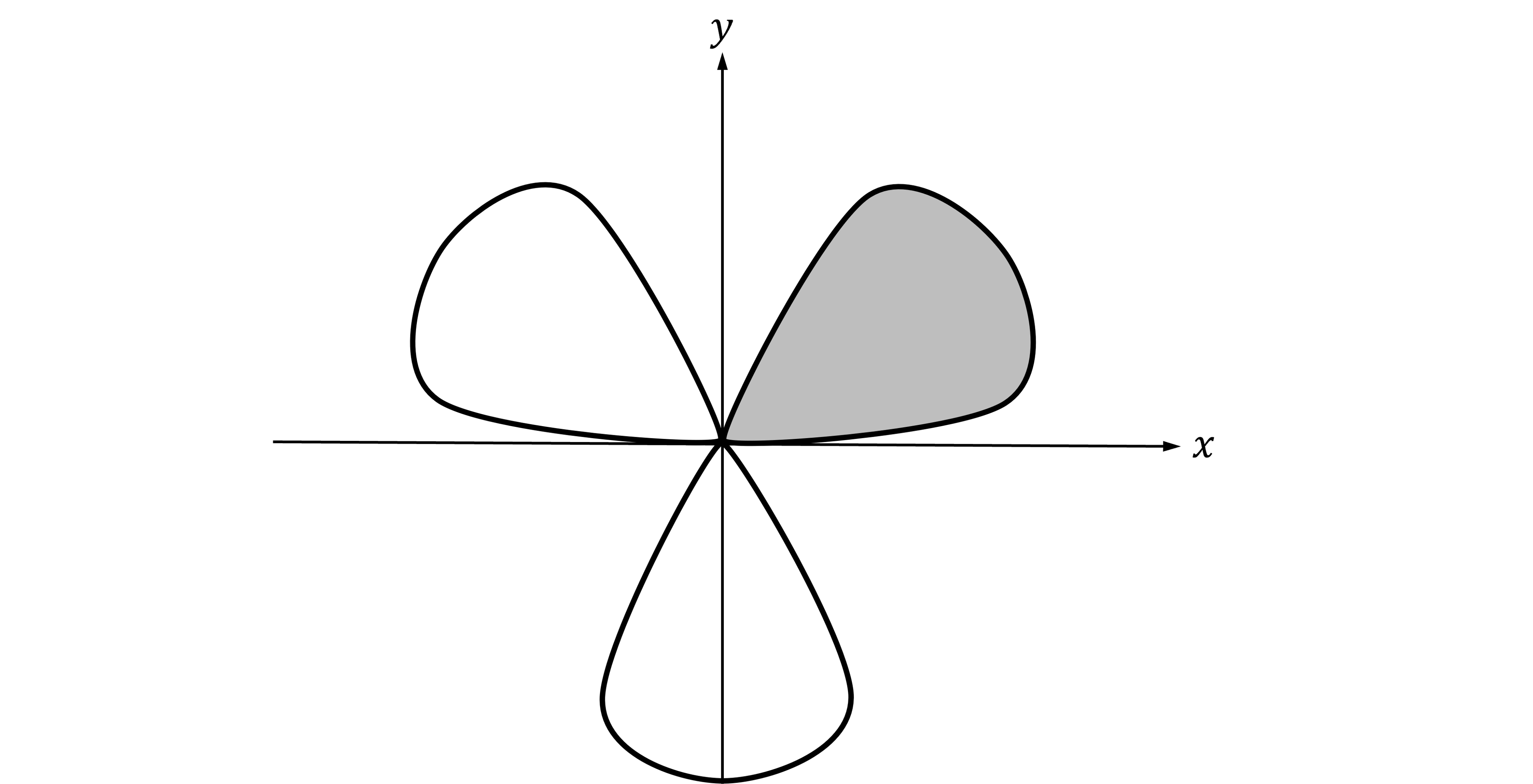
Graph of a polar plot with three symmetric petals (loops) around the origin; the top right petal is shaded grey, showing an area of interest.

(a) Find the area of the single shaded loop on the diagram.

The loop starts and ends when r equals 0 so substitute r equals 0 into r equals sin space 3 theta

0 equals sin space 3 theta

Solving this equation gives

table row cell 3 theta end cell equals cell 0 comma space pi comma space 2 pi comma space... end cell row theta equals cell 0 comma pi over 3 comma fraction numerator 2 pi over denominator 3 end fraction comma space... end cell end table

The first two rays are theta equals 0 and theta equals pi over 3 as shown

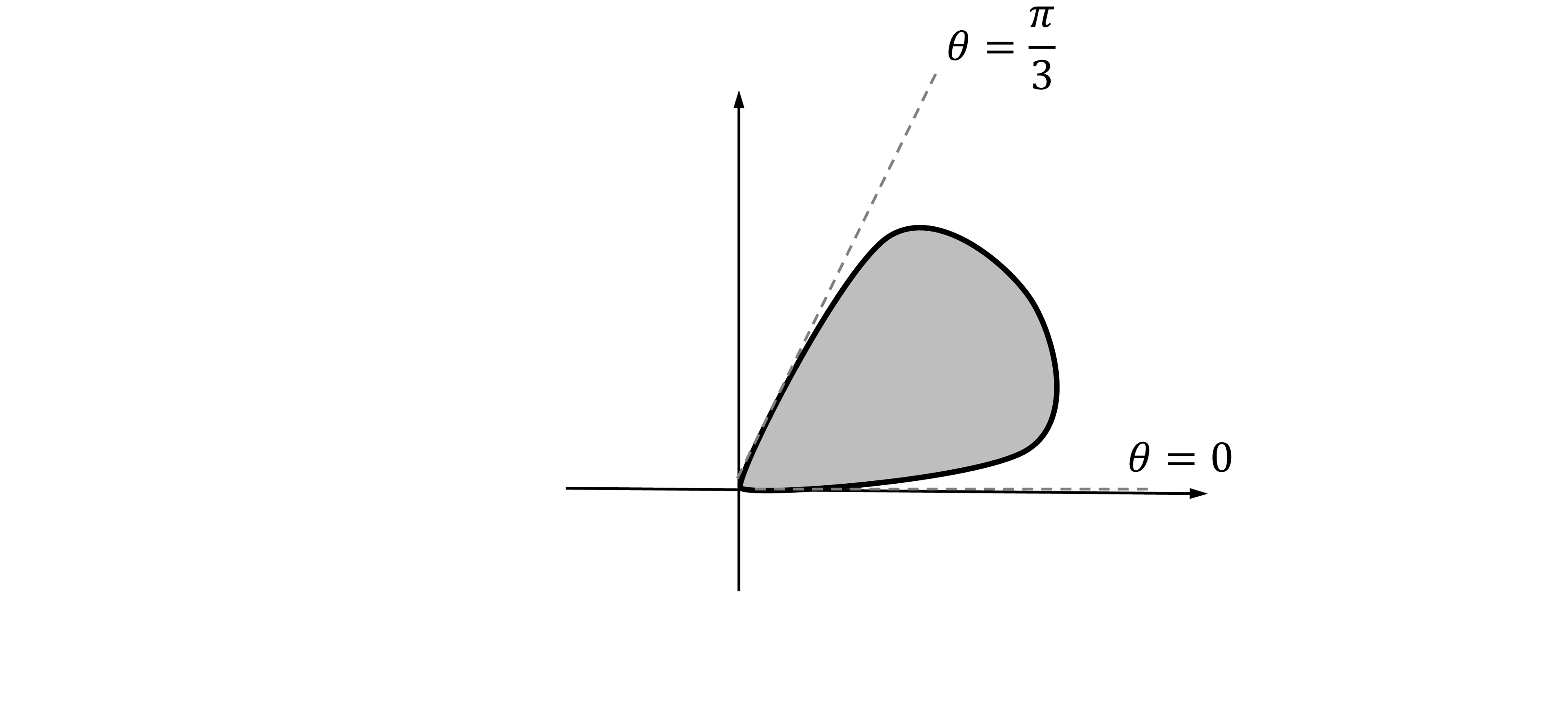
Graph showing a shaded area between θ=0 and θ=π/3 on polar coordinates with arrows indicating angles; the area is enclosed by a curve.

Substitute alpha equals 0, beta equals pi over 3 and r equals sin space 3 theta into the area formula, A equals integral subscript alpha superscript beta 1 half r squared space d theta

A equals integral subscript 0 superscript pi over 3 end superscript 1 half open parentheses sin space 3 theta close parentheses squared space d theta

Evaluate this definite integral on your calculator

0.261799...

The area of the single shaded loop is 0.262

(b) Write down the definite integral that represents the area enclosed by the loop below the x-axis.

From part (a), r equals 0 when table row theta equals cell 0 comma pi over 3 comma fraction numerator 2 pi over denominator 3 end fraction comma space... end cell end table

The loop in part (a) is between theta equals 0 and theta equals pi over 3, where r equals sin space 3 theta greater or equal than 0, so r greater or equal than 0

The loop in this question is between theta equals pi over 3 and beta equals fraction numerator 2 pi over denominator 3 end fraction , where r equals sin space 3 theta less or equal than 0, so r is negative, r less or equal than 0, shown below

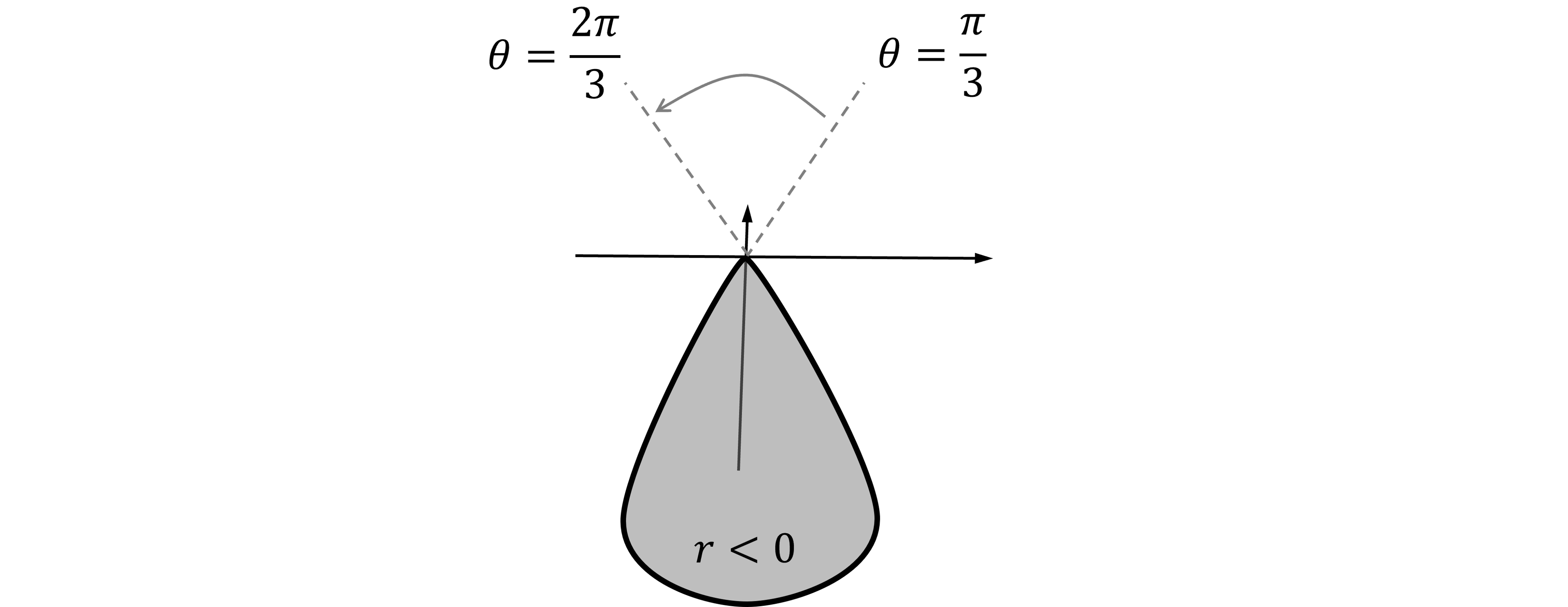
Diagram showing a grey loop under the x-axis with negative radius, with angles θ = π/3 and θ = 2π/3 marked with dashed lines.

However, the formula A equals integral subscript alpha superscript beta 1 half r squared space d theta still works for negative values of r (as r is squared in the integral), so substitute in alpha equals pi over 3, beta equals fraction numerator 2 pi over denominator 3 end fraction and r equals sin space 3 theta

A equals integral subscript pi over 3 end subscript superscript fraction numerator 2 pi over denominator 3 end fraction end superscript 1 half open parentheses sin space 3 theta close parentheses squared space d theta

(c) Find the total area enclosed by the curve.

The total area enclosed by the curve will be the area of 3 loops

Multiply the answer in part (a) by 3

3 cross times 0.261799... equals 0.7853...

The total area enclosed is 0.785

You've read 0 of your 5 free study guides this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Derivatives of Polar CurvesNext:Areas between Two Polar Curves
    Author
    Reviewer
    Mark Curtis

    Author: Mark Curtis

    Expertise: Maths Content Creator

    Mark graduated twice from the University of Oxford: once in 2009 with a First in Mathematics, then again in 2013 with a PhD (DPhil) in Mathematics. He has had nine successful years as a secondary school teacher, specialising in A-Level Further Maths and running extension classes for Oxbridge Maths applicants. Alongside his teaching, he has written five internal textbooks, introduced new spiralling school curriculums and trained other Maths teachers through outreach programmes.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.