Areas between Two Polar Curves (College Board AP® Calculus BC)

Study Guide

Written by: Mark Curtis

Reviewed by: Dan Finlay

Updated on 23 January 2025

Areas between two polar curves

How do I find an area between two polar curves?

To find an area between two polar curves, $r = f (θ)$ and $r = g (θ)$ :
- Sketch the two curves
- Find the angle(s) of intersection, $θ = α$
  - by solving $f (θ) = g (θ)$
- Draw a ray in the direction of $θ = α$ on your diagram
  - This is a straight line from the pole to the point of intersection
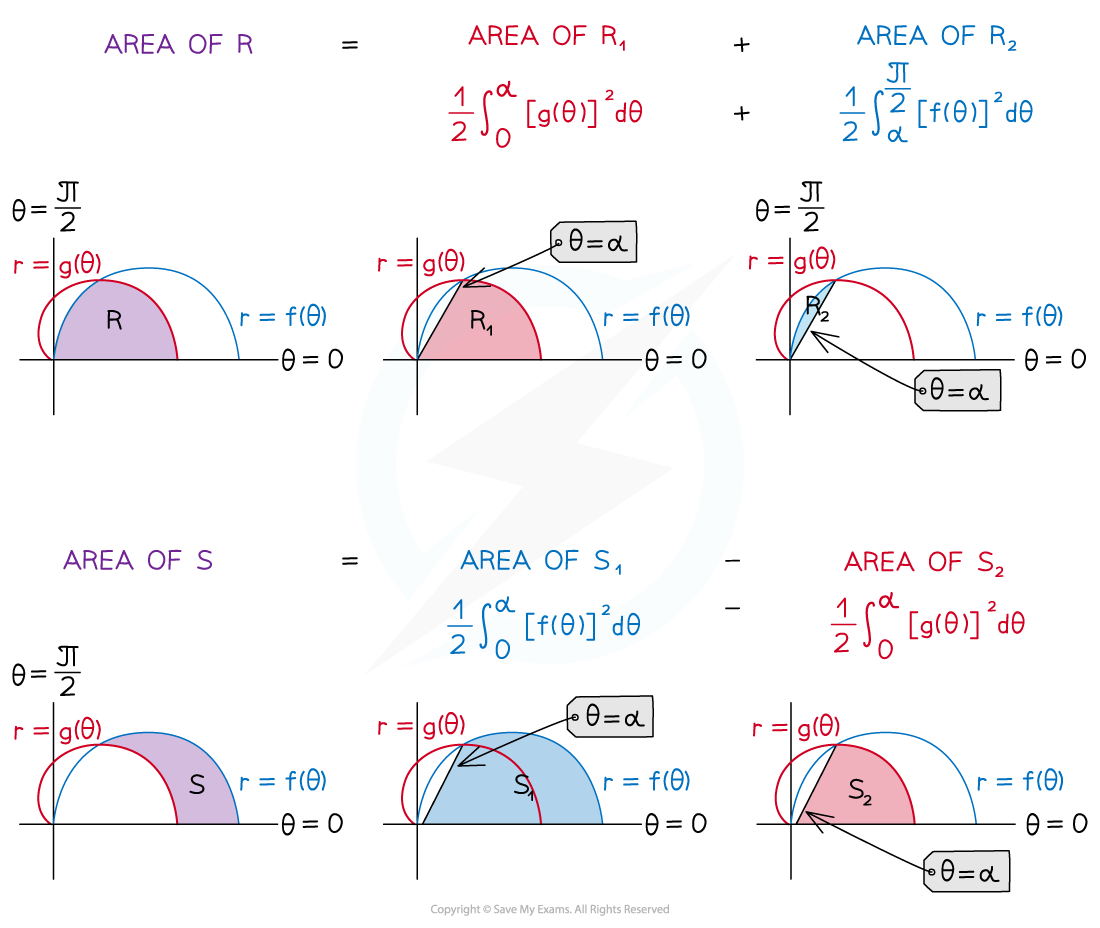
- Split the area into either a sum or difference of two polar areas, for example:
  - Region R shown below is a sum
  - Region S shown below is difference
- Use the area formula $A = \int_{θ_{1}}^{θ_{2}} \frac{1}{2} r^{2} d θ$ to find each area

7-1-2-edexcel-al-fm-polar-multiple-areas

Examiner Tips and Tricks

If one of the polar areas is part of a circle, e.g. the circle $r = a$ , then it can be quicker to use the formula for the area of a circle, $π a^{2}$ .

Worked Example

A sketch of the polar curves $r = 1 + \cos θ$ and $r = 3 \cos θ$ where $0 \leq θ \leq \frac{π}{2}$ is shown below.

The shaded region is labeled $R_{1}$ and an unshaded region is labeled $R_{2}$ .

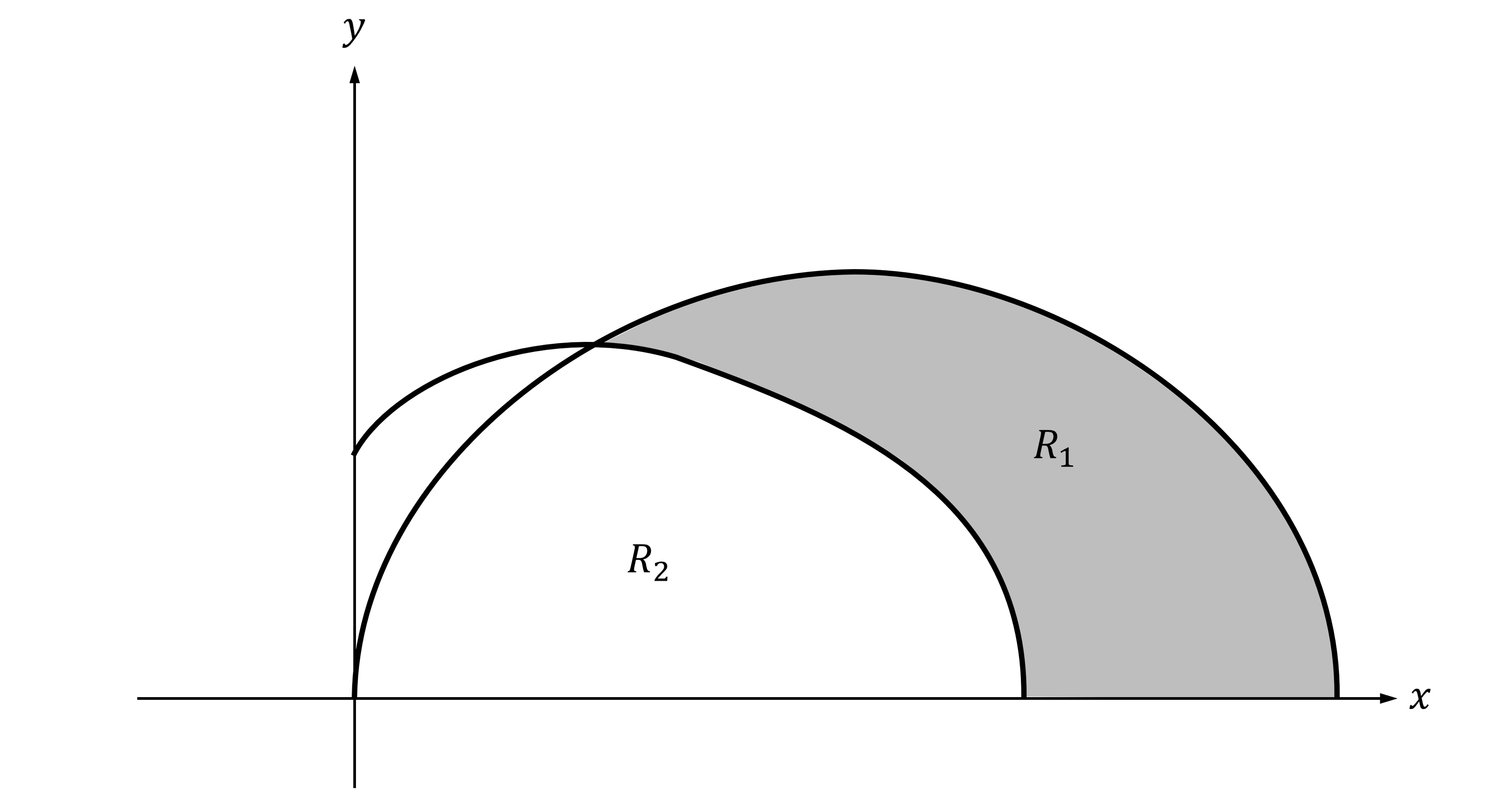
Graph showing two intersecting curves on axes, creating regions R1 and R2. Region R1 is shaded grey.

(a) Find the area of $R_{1}$ , leaving your answer as a single integral.

When $θ = 0$ , $r = 3 \cos θ$ is $3$ and $r = 1 + \cos θ$ is $2$ , so $r = 3 \cos θ$ is the larger curve

Find the angle at which the two curves intersect by setting $1 + \cos θ$ equal to $3 \cos θ$ and solving

$\begin{array}{rcl} 1 + \cos θ & = & 3 \cos θ \\ 1 & = & 2 \cos θ \\ \frac{1}{2} & = & \cos θ \\ θ & = & \frac{π}{3} \end{array}$

Draw the ray $θ = \frac{π}{3}$ on the diagram to see how to form the area $R_{1}$

It is the difference between the two polar areas shown below

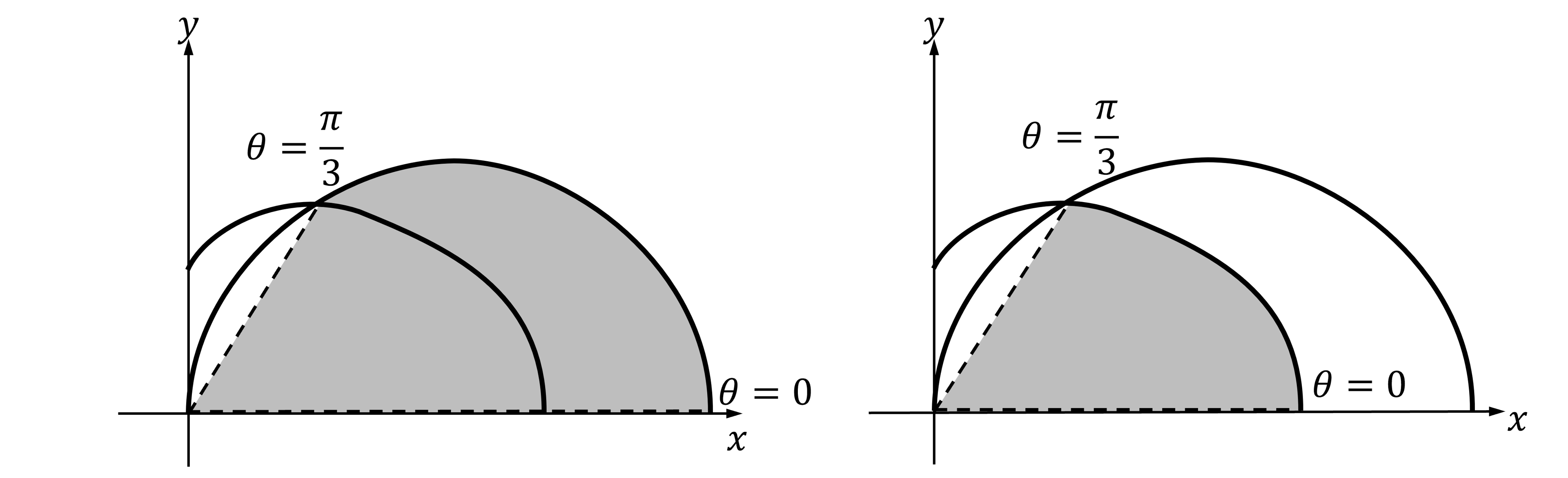
Two graphs showing a larger polar area from one curve on the left and a smaller polar area from the other curve on the right.

Use the formula $A = \int_{θ_{1}}^{θ_{2}} \frac{1}{2} r^{2} d θ$ to work out the two individual areas, then subtract the smaller area from the larger area

$\int_{0}^{\frac{π}{3}} \frac{1}{2} {(3 \cos θ)}^{2} d θ - \int_{0}^{\frac{π}{3}} \frac{1}{2} {(1 + \cos θ)}^{2} d θ$

The limits of the integrals are the same, so the integrals can be joined to form one single integral (as requested by the question)

$\int_{0}^{\frac{π}{3}} \frac{1}{2} [{(3 \cos θ)}^{2} - {(1 + \cos θ)}^{2}] d θ$

(b) Find the area of $R_{2}$ .

$R_{2}$ is the sum of the two polar areas shown below

$r = 1 + \cos θ$ gives the part of the area from $θ = 0$ to the point of intersection

$r = 3 \cos θ$ gives the part of the area from the point of intersection to $θ = \frac{π}{2}$ (where $r = 0$ ), which is the end of the range given in the question

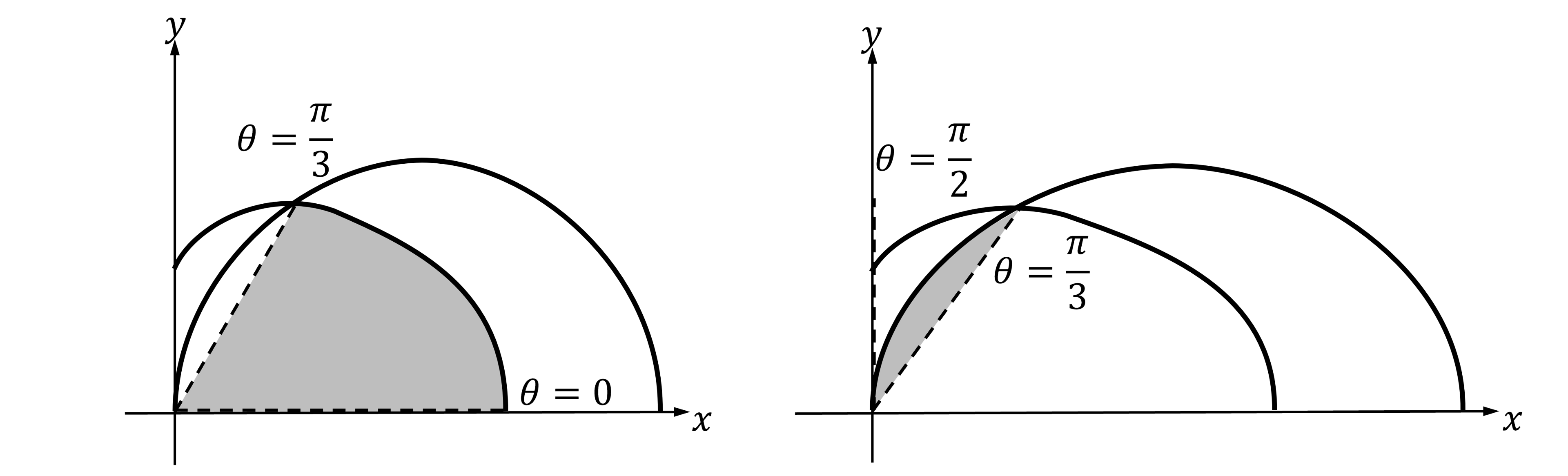
Two graphs, where the one on the left shows a polar region enclosed by one of the graphs and the one on the right shows a different polar region, which, when added to the first, gives the total area required.

Use the formula $A = \int_{θ_{1}}^{θ_{2}} \frac{1}{2} r^{2} d θ$ to work out the two individual areas, then add them together

$\int_{0}^{\frac{π}{3}} \frac{1}{2} {(1 + \cos θ)}^{2} d θ + \int_{\frac{π}{3}}^{\frac{π}{2}} \frac{1}{2} {(3 \cos θ)}^{2} d θ$

Evaluate the integrals above on your calculator

$1.759676 . . . + 0.203818 . . .$

$1.963$

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Did this page help you?

Previous:Areas from a Single Polar CurveNext:Convergent & Divergent Infinite Series

Areas between Two Polar Curves (College Board AP® Calculus BC)

Study Guide

Areas between two polar curves

How do I find an area between two polar curves?

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

Unit 1: Limits & Continuity

Limits

Definition of a Limit

Infinite Limits & Limits at Infinity

Properties of Limits

Evaluating Limits Analytically

Evaluating Limits Numerically & Graphically

Squeeze Theorem & Trigonometric Limits

Summary of Limits

Selecting Procedures for Determining Limits

Continuity

Continuity

Removable Discontinuities

Non-removable Discontinuities

Intermediate Value Theorem

Unit 2: Differentiation Definition & Fundamental Properties

Definition of Differentiation

Average Rate of Change

Instantaneous Rate of Change

Derivatives & Tangents

Estimating the Derivative at a Point

Differentiability & Continuity

Fundamental Properties of Differentiation

Derivative Rules

Derivatives of Exponentials and Logarithms

Derivatives of Sine and Cosine Functions

The Product Rule

The Quotient Rule

Derivatives of Tangent and Reciprocal Trig Functions

Unit 3: Differentiation of Composite, Implicit & Inverse Functions

Differentiation of Composite & Inverse Functions

The Chain Rule

The Inverse Function Theorem

Derivatives of Inverse Trigonometric Functions

Higher-Order Derivatives

Summary of Differentiation

Selecting Procedures for Calculating Derivatives

Unit 4: Contextual Applications of Differentiation

Rates of Change & Related Rates

Meaning of a Derivative in Context

Motion in a Straight Line

Related Rates

Linearization

Approximating Values of a Function

L'Hospital's Rule

L'Hospital's Rule

Unit 5: Analytical Applications of Differentiation

Graphs of Functions & Their Derivatives

Mean Value Theorem

Extreme Value Theorem

Critical Points

Increasing & Decreasing Functions

First Derivative Test for Local Extrema

Candidates Test for Global Extrema

Concavity of Functions

Second Derivative Test for Local Extrema

Graphs of f, f' & f''

Optimization Problems

Behaviors of Implicit Relations

Second Derivatives of Implicit Functions

Critical Points of Implicit Relations

Unit 6: Integration & Accumulation of Change

Integration & Antiderivatives

Indefinite Integrals

Derivatives & Antiderivatives

Indefinite Integral Rules

Constant of Integration

Riemann Sums & Definite Integrals

Accumulation of Change

Riemann Sums

Trapezoidal sums

Accumulation Functions

Fundamental Theorem of Calculus

Properties of Definite Integrals