Derivatives of Parametric Equations (College Board AP® Calculus BC)

Study Guide

Written by: Mark Curtis

Reviewed by: Dan Finlay

Updated on 24 January 2025

Derivatives of parametric equations

What is the parametric first derivative?

The parametric first derivative is given by the formula:

$\frac{d y}{d x} = \frac{\frac{d y}{d t}}{\frac{d x}{d t}}$

This gives the slope of a line that is tangent to a parametric curve at the point with $t = t_{0}$

Graph with a parametric curve and its tangent at point P, marked at time t equals t0; formula shows derivative of y with respect to x.

It comes from $\frac{d y}{d x} = \frac{d y}{d t} \times \frac{d t}{d x} = \frac{d y}{d t} \times \frac{1}{\frac{d x}{d t}}$
You can use it provided $\frac{d x}{d t} \neq 0$ at $t = t_{0}$ (to avoid division by zero)

How do I calculate the parametric first derivative?

For example, to find $\frac{d y}{d x}$ at $t = 4$ on the curve given by $x = t + e^{t}$ and $y = t^{2} + 3$ :
- Differentiate the parametric equations individually
  - $\frac{d x}{d t} = 1 + e^{t}$ and $\frac{d y}{d t} = 2 t$
- Substitute them into the parametric first derivative, getting the order correct
  - $\frac{d y}{d x} = \frac{\frac{d y}{d t}}{\frac{d x}{d t}} = \frac{2 t}{1 + e^{t}}$
- Evaluate this at $t = 4$ :
  - $\frac{d y}{d x} = \frac{2 \times 4}{1 + e^{4}} = \frac{8}{1 + e^{4}}$

Examiner Tips and Tricks

You may be asked to find the equation of the line tangent to a parametric curve at a particular point, which requires calculating the parametric first derivative.

How do I find horizontal and vertical tangents?

Graph showing a curve with two horizontal tangents where dy/dt=0, and one vertical tangent where dx/dt=0, indicated.

A horizontal tangent occurs at a point $t = t_{0}$ when $\frac{d y}{d t} = 0$ at $t = t_{0}$
- and $\frac{d x}{d t} \neq 0$ at $t = t_{0}$
- Substituting these into the parametric first derivative formula gives zero

A vertical tangent occurs at a point $t = t_{0}$ when $\frac{d x}{d t} = 0$ at $t = t_{0}$
- and $\frac{d y}{d t} \neq 0$ at $t = t_{0}$
- Substituting these into the parametric first derivative formula gives an infinite value
If both $\frac{d x}{d t} = \frac{d y}{d t} = 0$ at $t = t_{0}$ then the limit of $\frac{d y}{d x} = \frac{\frac{d y}{d t}}{\frac{d x}{d t}} (= \frac{0}{0})$ needs further investigation

Examiner Tips and Tricks

If asked to find any local maxima, minima or points of inflection on a parametric curve, start by finding all the points at which the tangent is horizontal (then investigate further, e.g. with a sketch or second-derivative method).

Worked Example

A curve is given parametrically by

$\begin{array}{rcl} x & = & t^{3} - 12 t \\ y & = & t^{3} + 3 t \end{array}$

Part of the curve is shown below.

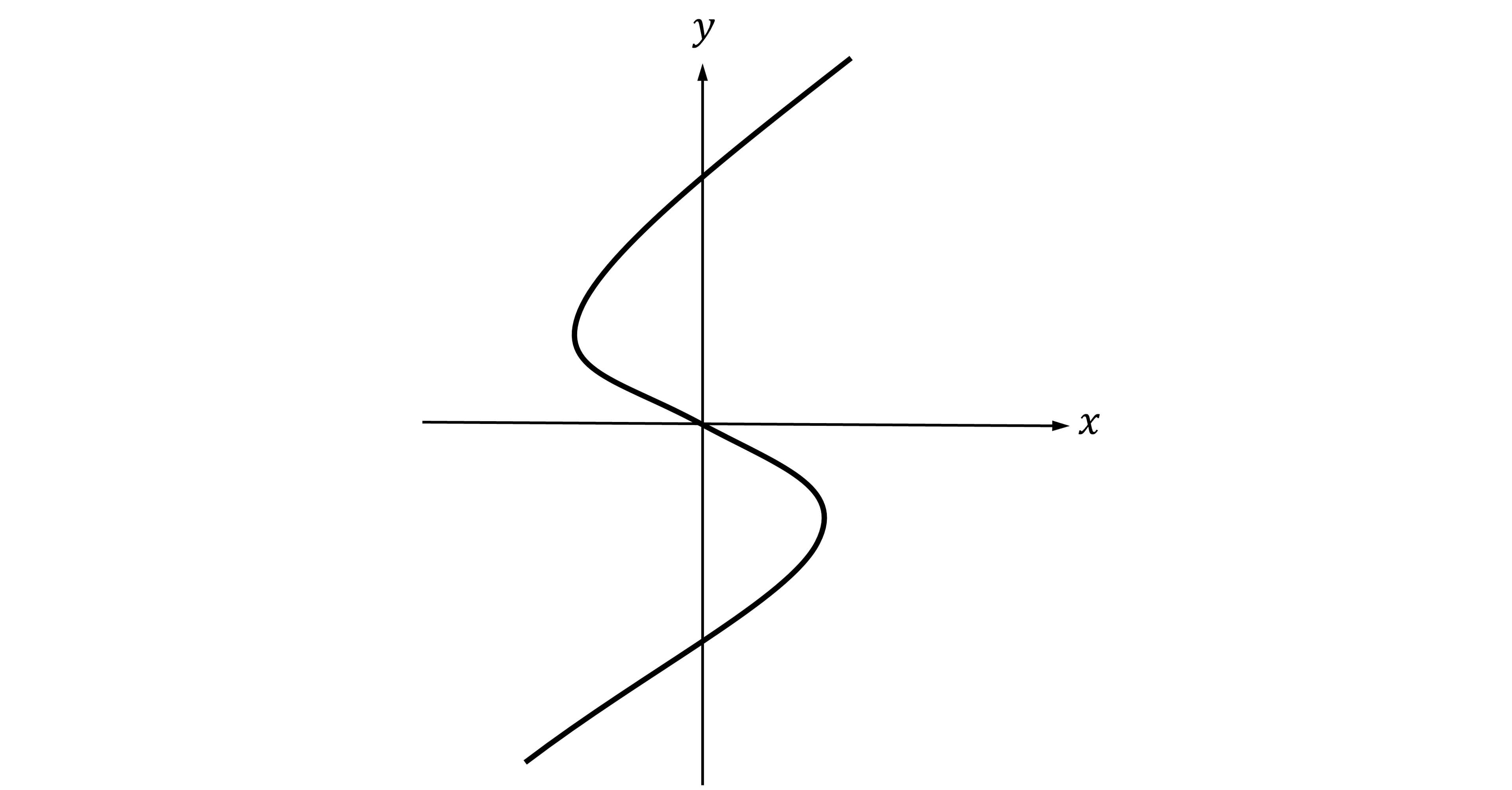
Graph showing a curve on x and y axes. The curve crosses the y-axis three times, passing through the origin, forming an S-shape, and extends beyond the axes.

(a) Find the slope of the line that is tangent to the curve at $t = 3$ .

You need to use the parametric first derivative, $\frac{d y}{d x} = \frac{\frac{d y}{d t}}{\frac{d x}{d t}}$

First, differentiate the parametric equations individually

$\begin{array}{rcl} \frac{d x}{d t} & = & 3 t^{2} - 12 \\ \frac{d y}{d t} & = & 3 t^{2} + 3 \end{array}$

Then substitute these derivatives into the formula, with $\frac{d y}{d t}$ on the top and $\frac{d x}{d t}$ on the bottom

$\frac{d y}{d x} = \frac{\frac{d y}{d t}}{\frac{d x}{d t}} = \frac{3 t^{2} + 3}{3 t^{2} - 12}$

Substitute in the parameter $t = 3$ and simplify

$\frac{d y}{d x} = \frac{3 (3^{2}) + 3}{3 (3^{2}) - 12} = \frac{30}{15} = 2$

The slope of the line that is tangent to the curve at $t = 3$ is 2

(b) Find the values of $t$ at which the tangent to the curve is vertical. Find the equations of these tangents.

Vertical tangents are points when $\frac{d x}{d t} = 0$ and $\frac{d y}{d t} \neq 0$

Set $\frac{d x}{d t} = 0$ and solve

$\begin{array}{rcl} 3 t^{2} - 12 & = & 0 \\ t^{2} & = & 4 \\ t & = & \pm 2 \end{array}$

Check that $\frac{d y}{d t} \neq 0$ by substituting $t = \pm 2$ into $\frac{d y}{d t}$

$\frac{d y}{d t} = 3 {(\pm 2)}^{2} + 3 = 15 \neq 0$

To find the equations of the vertical tangents, remember that vertical lines have the equations $x = k$ where $k$ is a constant

Substitute $t = \pm 2$ into $x = t^{3} - 12 t$

$2^{3} - 12 (2) = - 16$ and ${(- 2)}^{3} - 12 (- 2) = 16$

The point at $t = 2$ has a vertical tangent with equation $x = - 16$

The point at $t = - 2$ has a vertical tangent with equation $x = 16$

Horizontal tangents are points when $\frac{d y}{d t} = 0$ and $\frac{d x}{d t} \neq 0$

Set $\frac{d y}{d t} = 0$ and try to solve

$\begin{array}{rcl} 3 t^{2} + 3 & = & 0 \\ t^{2} & = & - 1 \end{array}$

There are no solutions to this equation as you cannot square root a negative number

There is no value of $t$ for which $\frac{d y}{d t} = 0$ so no horizontal tangents

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Did this page help you?

Previous:Defining Parametric EquationsNext:Second Derivatives of Parametric Equations

Derivatives of Parametric Equations (College Board AP® Calculus BC)

Study Guide

Derivatives of parametric equations

What is the parametric first derivative?

How do I calculate the parametric first derivative?

How do I find horizontal and vertical tangents?

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

Unit 1: Limits & Continuity

Limits

Definition of a Limit

Infinite Limits & Limits at Infinity

Properties of Limits

Evaluating Limits Analytically

Evaluating Limits Numerically & Graphically

Squeeze Theorem & Trigonometric Limits

Summary of Limits

Selecting Procedures for Determining Limits

Continuity

Continuity

Removable Discontinuities

Non-removable Discontinuities

Intermediate Value Theorem

Unit 2: Differentiation Definition & Fundamental Properties

Definition of Differentiation

Average Rate of Change

Instantaneous Rate of Change

Derivatives & Tangents

Estimating the Derivative at a Point

Differentiability & Continuity

Fundamental Properties of Differentiation

Derivative Rules

Derivatives of Exponentials and Logarithms

Derivatives of Sine and Cosine Functions

The Product Rule

The Quotient Rule

Derivatives of Tangent and Reciprocal Trig Functions

Unit 3: Differentiation of Composite, Implicit & Inverse Functions

Differentiation of Composite & Inverse Functions

The Chain Rule

The Inverse Function Theorem

Derivatives of Inverse Trigonometric Functions

Higher-Order Derivatives

Summary of Differentiation

Selecting Procedures for Calculating Derivatives

Unit 4: Contextual Applications of Differentiation

Rates of Change & Related Rates

Meaning of a Derivative in Context

Motion in a Straight Line

Related Rates

Linearization

Approximating Values of a Function

L'Hospital's Rule

L'Hospital's Rule

Unit 5: Analytical Applications of Differentiation

Graphs of Functions & Their Derivatives

Mean Value Theorem

Extreme Value Theorem

Critical Points

Increasing & Decreasing Functions

First Derivative Test for Local Extrema

Candidates Test for Global Extrema

Concavity of Functions

Second Derivative Test for Local Extrema

Graphs of f, f' & f''

Optimization Problems

Behaviors of Implicit Relations

Second Derivatives of Implicit Functions

Critical Points of Implicit Relations

Unit 6: Integration & Accumulation of Change

Integration & Antiderivatives

Indefinite Integrals

Derivatives & Antiderivatives

Indefinite Integral Rules

Constant of Integration

Riemann Sums & Definite Integrals

Accumulation of Change

Riemann Sums

Trapezoidal sums

Accumulation Functions