Study GuidesPast Papers
AP®MathsCollege BoardCalculus BCStudy GuidesUnit 9: Parametric Equations, Vector-Valued Functions & Polar CoordinatesParametric EquationsDefining Parametric Equations

Defining Parametric Equations (College Board AP® Calculus BC)

Study Guide

Mark Curtis

Written by: Mark Curtis

Reviewed by: Dan Finlay

Updated on

Defining parametric equations

What are parametric equations?

  • Parametric equations are an alternative way to represent the equation of a curve using a third variable called a parameter

    • The letter t is often used for the parameter

    • The parametric equations are

      • x equals f open parentheses t close parentheses

      • y equals g open parentheses t close parentheses

  • For example

    • x equals t minus 5

    • y equals t squared plus e to the power of t

  • Sometimes a restricted range of t values is given

    • e.g. where 0 less or equal than t less or equal than 8

How do I sketch parametric equations?

Six graphs of parametric equations with x and y axes: including a circle, horizontal ellipse, spiral, a loop, a four-leaf rose and graph with cusps.

  • You can sketch parametric curves using your calculator

    • Change the type of graph to "parametric"

  • Parametric curves often have very interesting shapes

    • They can loop around and spiral etc.

  • Parametric curves have a direction of flow

    • e.g. anticlockwise around a loop

    • The direction can be found by looking at the equations as t increases

  • You can find key features of the graph algebraically

    • The y-intercepts are when x equals 0

      • If x equals f open parentheses t close parentheses then solve f open parentheses t close parentheses equals 0

    • The x-intercepts are when y equals 0

      • If y equals g open parentheses t close parentheses then solve g open parentheses t close parentheses equals 0

Examiner Tips and Tricks

If parametric equations involve trig functions (e.g. sin space t) then you should plot in radians on your calculator.

How do I eliminate the parameter?

  • Eliminating the parameter means rewriting a parametric curve as an equation in x and y only (no t)

    • To do this:

      • Make t the subject of one of the equations

      • Substitute this into the other equation

      • Simplify if required

    • e.g. make t the subject of x equals t minus 5 and substitute it into y equals t squared plus e to the power of t

      • This gives y equals open parentheses x plus 5 close parentheses squared plus e to the power of x plus 5 end exponent

      • There is no t

  • You may need to convert a range of t values into a range of x or y values

    • See the Worked Example

  • It is not always possible to eliminate the parameter

    • e.g. x equals t plus e to the power of t and y equals sin space t plus ln space t

    • If it is possible, it is not always possible to make y the subject

      • e.g. y e to the power of y equals x plus 1

How do I use trigonometric identities to eliminate the parameter?

  • Another way to eliminate the parameter is by substituting parametric equations into a trigonometric identity

    • e.g. rearrange and substitute x equals 2 plus sin space t and y equals 4 space cos space t into the identity sin squared space t plus cos squared space t equals 1

      • This gives the equation open parentheses x minus 2 close parentheses squared plus open parentheses y over 4 close parentheses squared equals 1

      • There is no t

Worked Example

A curve is given parametrically by

table row x equals cell 3 minus e to the power of t end cell row y equals cell 2 plus t end cell end table

where 0 less or equal than t less or equal than 2

(a) Find the coordinates of any points at which the curve intersects the coordinate axes.

To find any points of intersection with the x-axis, y must equal zero

2 plus t equals 0

Solve this equation to find t

t equals negative 2

However you are told 0 less or equal than t less or equal than 2 so t equals negative 2 is not possible (there is no x-intercept)

To find any points of intersection with the y-axis, x must equal zero

3 minus e to the power of t equals 0

Solve this equation to find t

e to the power of t equals 3 t equals ln space 3

Since ln space 3 equals 1.0986... this value of t is in the range 0 less or equal than t less or equal than 2

Substitute t equals ln space 3 into the equation for y to find its coordinate

y equals 2 plus t y equals 2 plus ln space 3

The only point at which the curve crosses the coordinate axes is open parentheses 0 comma space 2 plus ln space 3 close parentheses

(b) Sketch the curve. Indicate the direction of the curve as t increases.

Change the input in your calculator to "parametric" and use it to sketch the graph for 0 less or equal than t less or equal than 2

The direction can be found by looking at the coordinates of two points as t increases, e.g. t equals 0 and t equals 2

When t equals 0 then x equals 3 minus e to the power of 0 equals 3 minus 1 equals 2 and y equals 2 plus 0 equals 2, and when t equals 2 then x equals 3 minus e squared open parentheses equals negative 4.389056... close parentheses and y equals 2 plus 2 equals 4

t equals 0 gives coordinates open parentheses 2 comma space 2 close parentheses

t equals 2 gives coordinates open parentheses 3 minus e squared comma space 4 close parentheses

So direction of flow is from open parentheses 2 comma space 2 close parentheses to open parentheses 3 minus e squared comma space 4 close parentheses

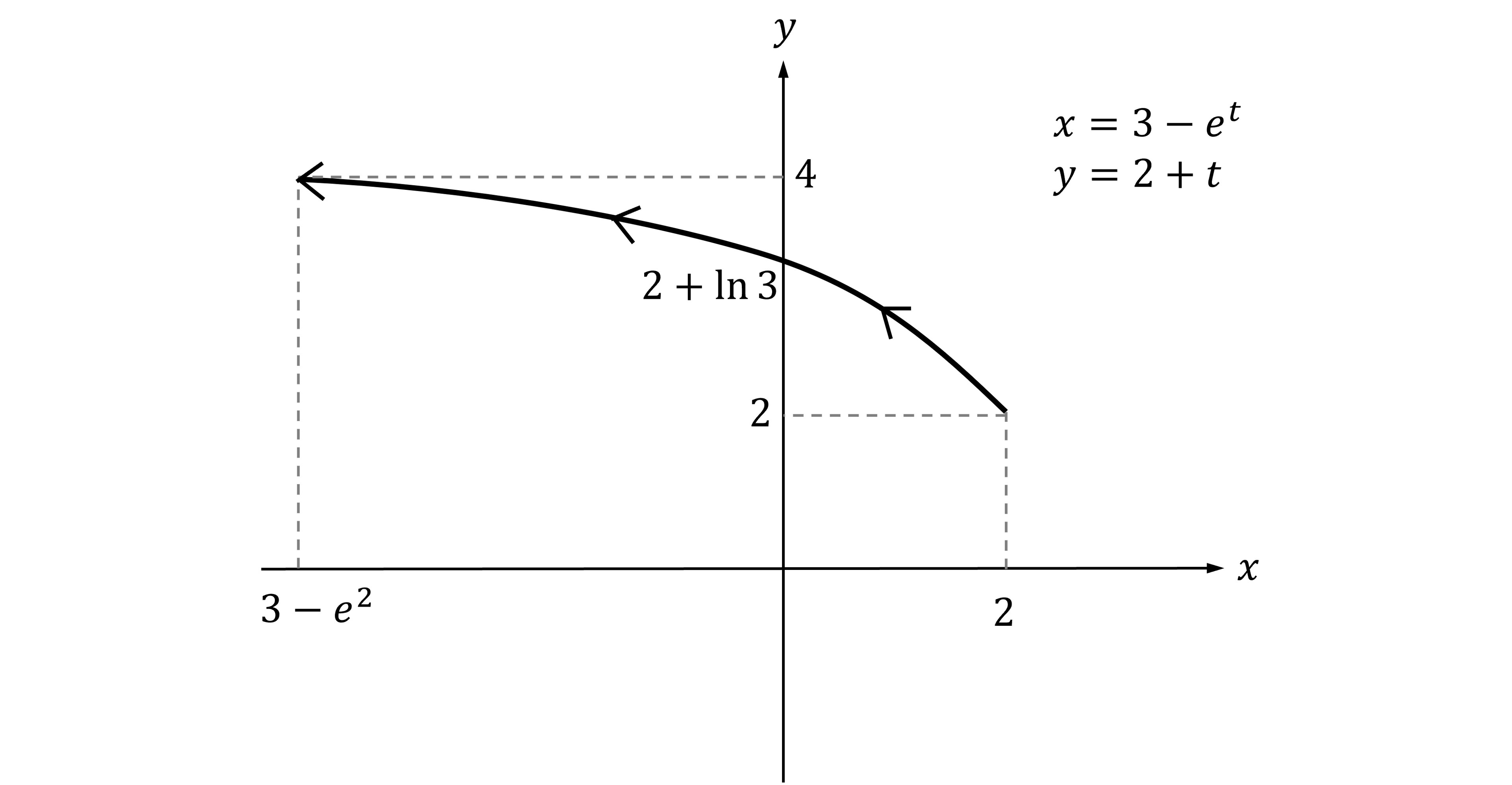
Graph of parametric equations x = 3 - e^t and y = 2 + t showing a curved line with arrows, dashed lines to axes, and marked points.

(c) Find the equation of the curve in the form y equals f open parentheses x close parentheses.

The form asked for has no t in it, so make t the subject of one of the equations and substitute it into the other

For example, make t the subject of the x equation

table row x equals cell 3 minus e to the power of t end cell row cell e to the power of t end cell equals cell 3 minus x end cell row t equals cell ln open parentheses 3 minus x close parentheses end cell end table

Then substitute this into the y equation

table row y equals cell 2 plus t end cell row y equals cell 2 plus ln open parentheses 3 minus x close parentheses end cell end table

The range 0 less or equal than t less or equal than 2 needs to be turned into a range of x values (for example, by looking at the x-axis in the graph above)

y equals 2 plus ln open parentheses 3 minus x close parentheses where 3 minus e squared less or equal than x less or equal than 2

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Did this page help you?

    Previous:Washer Method Around Other AxesNext:Derivatives of Parametric Equations
    Author
    Reviewer
    Mark Curtis

    Author: Mark Curtis

    Expertise: Maths

    Mark graduated twice from the University of Oxford: once in 2009 with a First in Mathematics, then again in 2013 with a PhD (DPhil) in Mathematics. He has had nine successful years as a secondary school teacher, specialising in A-Level Further Maths and running extension classes for Oxbridge Maths applicants. Alongside his teaching, he has written five internal textbooks, introduced new spiralling school curriculums and trained other Maths teachers through outreach programmes.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.