Study GuidesExam QuestionsPast Papers
AP®MathsCollege BoardCalculus BCStudy GuidesUnit 10: Infinite Sequences and SeriesTests for Divergence & ConvergenceIntegral Test for Convergence

Integral Test for Convergence (College Board AP® Calculus BC): Study Guide

Roger B

Written by: Roger B

Reviewed by: Mark Curtis

Updated on

Integral test

What is the integral test?

  • The integral test is a method of determining whether an infinite series converges or diverges

  • Let a subscript n equals f open parentheses n close parentheses, where f is a continuous, positive, decreasing function on left square bracket c comma space infinity right parenthesis

    • Then the series sum from n equals c to infinity of a subscript n converges if the improper integral integral subscript c superscript infinity f open parentheses x close parentheses space d x exists

      • I.e. if the integral has a finite answer

    • If the improper integral doesn't exist then the series diverges

How does the integral test work?

  • Each term in the infinite series a subscript 1 plus a subscript 2 plus a subscript 3 plus... can be represented by the area of a rectangle of width 1 and height a subscript n

  • The integral integral subscript 1 superscript infinity f open parentheses x close parentheses space d x equals A represents the area Aunder the curve f open parentheses x close parentheses from x equals 1 to infinity

  • In the first image, A is an underestimate of the rectangles a subscript 1 plus a subscript 2 plus a subscript 3 plus...

    • so A less than sum from n equals 1 to infinity of a subscript n

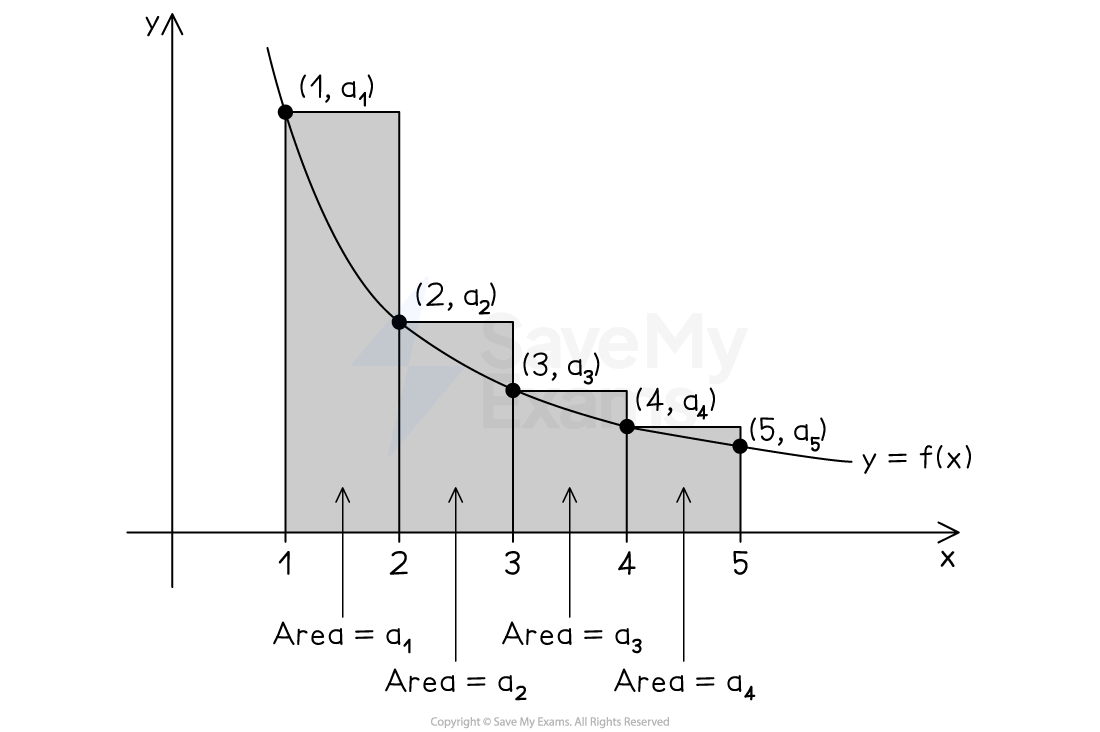
Graph showing a curve y=f(x) with marked points at intervals. Grey rectangles overestimate the area under the graph and the areas a1 to a5 represent the infinite series.

  • In the next image, A is an overestimate of the rectangles a subscript 2 plus a subscript 3 plus...

    • Adding a subscript 1 to both sides gives a subscript 1 plus A greater than sum from n equals 1 to infinity of a subscript n

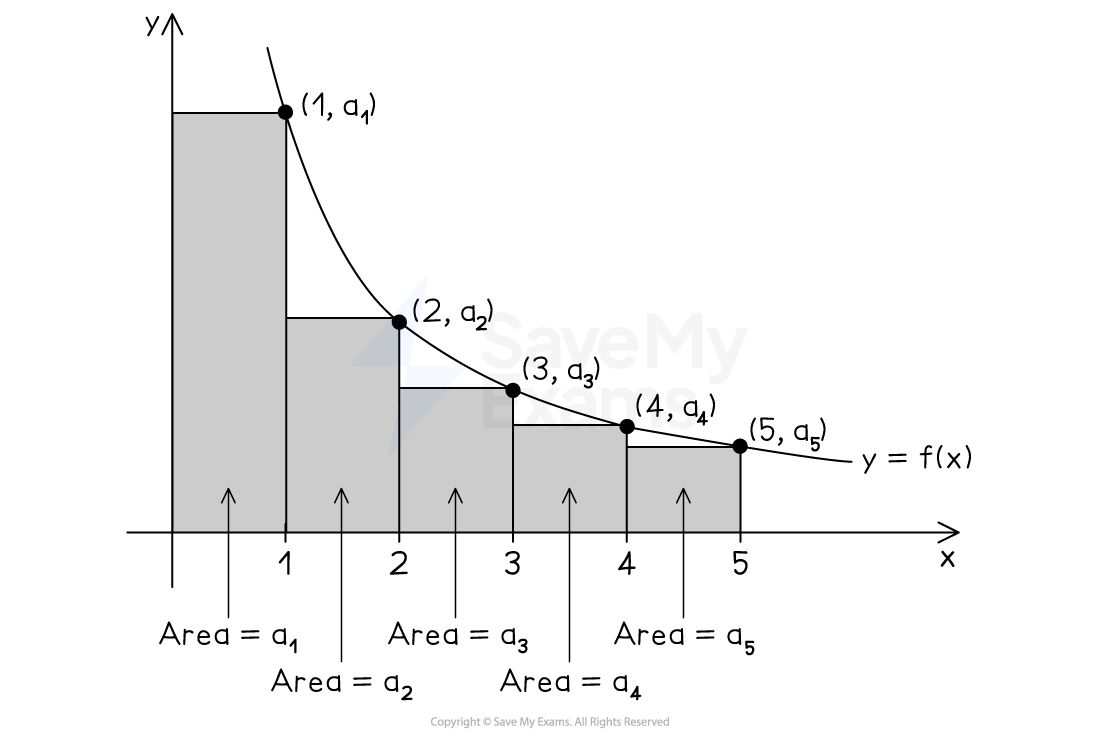
Graph showing a curve y=f(x) with decreasing step-like shaded rectangular areas under it representing the infinite series. Points (1,a1) to (5,a5) are marked. Axes labelled x and y.

  • So A less than sum from n equals 1 to infinity of a subscript n less than A plus a subscript 1 which means

    • if A is finite then sum from n equals 1 to infinity of a subscript n must have a finite value (the series converges)

    • if A is infinite then sum from n equals 1 to infinity of a subscript n must also be infinite (the series diverges)

Worked Example

Use the integral test to determine whether each of the following series converges or diverges.

(a) sum from n equals 1 to infinity of 1 over n

Note that this series is the harmonic series 1 plus 1 half plus 1 third plus 1 fourth plus...

Evaluate the improper integral integral subscript 1 superscript infinity 1 over x space d x

table row cell integral subscript 1 superscript infinity 1 over x space d x end cell equals cell limit as p rightwards arrow infinity of integral subscript 1 superscript p 1 over x space d x end cell row blank equals cell limit as p rightwards arrow infinity of open square brackets ln open vertical bar x close vertical bar close square brackets subscript 1 superscript p end cell row blank equals cell limit as p rightwards arrow infinity of open parentheses ln p minus ln 1 close parentheses end cell row blank equals cell limit as p rightwards arrow infinity of ln p end cell row blank equals infinity end table

The improper integral diverges to infinity (as logarithmic growth tends to infinity, ln space x rightwards arrow infinity as x rightwards arrow infinity), so the series diverges

The integral integral subscript 1 superscript infinity 1 over x space d x diverges to infinity, so by the integral test the series is divergent

(b) sum from n equals 1 to infinity of 1 over n squared

Note that this is a p-series with p equals 2

Evaluate the improper integral integral subscript 1 superscript infinity 1 over x squared space d x

table row cell integral subscript 1 superscript infinity 1 over x squared space d x end cell equals cell limit as p rightwards arrow infinity of integral subscript 1 superscript p x to the power of negative 2 end exponent space d x end cell row blank equals cell limit as p rightwards arrow infinity of open square brackets negative x to the power of negative 1 end exponent close square brackets subscript 1 superscript p end cell row blank equals cell limit as p rightwards arrow infinity of open square brackets negative 1 over x close square brackets subscript 1 superscript p end cell row blank equals cell limit as p rightwards arrow infinity of open parentheses negative 1 over p minus open parentheses negative 1 over 1 close parentheses close parentheses end cell row blank equals cell limit as p rightwards arrow infinity of open parentheses 1 minus 1 over p close parentheses end cell row blank equals cell 1 minus 0 end cell row blank equals 1 end table

The improper integral converges to a finite value, so the series converges

The integral integral subscript 1 superscript infinity 1 over x squared space d x exists with a finite value, so by the integral test the series is convergent

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:nth Term Test for DivergenceNext:Comparison Tests for Convergence
    Author
    Reviewer
    Roger B

    Author: Roger B

    Expertise: Maths

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

    Mark Curtis

    Author: Mark Curtis

    Expertise: Maths

    Mark graduated twice from the University of Oxford: once in 2009 with a First in Mathematics, then again in 2013 with a PhD (DPhil) in Mathematics. He has had nine successful years as a secondary school teacher, specialising in A-Level Further Maths and running extension classes for Oxbridge Maths applicants. Alongside his teaching, he has written five internal textbooks, introduced new spiralling school curriculums and trained other Maths teachers through outreach programmes.