Study GuidesExam QuestionsPast Papers
AP®MathsCollege BoardCalculus BCStudy GuidesUnit 10: Infinite Sequences and SeriesSeries Representations of FunctionsTaylor Polynomial Approximation of a Function

Taylor Polynomial Approximation of a Function (College Board AP® Calculus BC): Study Guide

Roger B

Written by: Roger B

Reviewed by: Mark Curtis

Updated on

Taylor & Maclaurin polynomials

What is a Taylor polynomial approximation of a function?

  • A Taylor approximation about the point x equals a is a way of approximating a function near to that point using a polynomial

    • This polynomial is called a Taylor polynomial

  • Let f be a function

    • If the function and its first n derivatives all exist at x equals a, then the nth degree Taylor polynomial for f about x equals a is

space p subscript n open parentheses x close parentheses equals f open parentheses a close parentheses plus f to the power of apostrophe open parentheses a close parentheses open parentheses x minus a close parentheses plus fraction numerator f to the power of apostrophe apostrophe end exponent open parentheses a close parentheses over denominator 2 factorial end fraction open parentheses x minus a close parentheses squared plus... plus fraction numerator f to the power of open parentheses n close parentheses end exponent open parentheses a close parentheses over denominator n factorial end fraction open parentheses x minus a close parentheses to the power of n

  • Note that

    • space p subscript n open parentheses a close parentheses equals f open parentheses a close parentheses plus f to the power of apostrophe open parentheses a close parentheses open parentheses a minus a close parentheses plus fraction numerator f to the power of apostrophe apostrophe end exponent open parentheses a close parentheses over denominator 2 factorial end fraction open parentheses a minus a close parentheses squared plus... plus fraction numerator f to the power of open parentheses n close parentheses end exponent open parentheses a close parentheses over denominator n factorial end fraction open parentheses a minus a close parentheses to the power of n equals f open parentheses a close parentheses

      • I.e. a Taylor polynomial is always exactly equal to its function at x equals a

    • space p subscript 1 open parentheses x close parentheses equals f open parentheses a close parentheses plus f to the power of apostrophe open parentheses a close parentheses open parentheses x minus a close parentheses

      • This is the equation of a line with slope f to the power of apostrophe open parentheses a close parentheses, that goes through the point open parentheses a comma space f open parentheses a close parentheses close parentheses

      • I.e. the first-degree Taylor polynomial is the equation of the tangent line to the graph of f at the point open parentheses a comma space f open parentheses a close parentheses close parentheses

  • For example, the first few Taylor polynomials for f open parentheses x close parentheses equals ln x about x equals 2 are:

    • space p subscript 1 open parentheses x close parentheses equals ln 2 plus fraction numerator x minus 2 over denominator 2 end fraction

    • space p subscript 2 open parentheses x close parentheses equals ln 2 plus fraction numerator x minus 2 over denominator 2 end fraction minus open parentheses x minus 2 close parentheses squared over 8

    • space p subscript 3 open parentheses x close parentheses equals ln 2 plus fraction numerator x minus 2 over denominator 2 end fraction minus open parentheses x minus 2 close parentheses squared over 8 plus open parentheses x minus 2 close parentheses cubed over 24

    • space p subscript 4 open parentheses x close parentheses equals ln 2 plus fraction numerator x minus 2 over denominator 2 end fraction minus open parentheses x minus 2 close parentheses squared over 8 plus open parentheses x minus 2 close parentheses cubed over 24 minus open parentheses x minus 2 close parentheses to the power of 4 over 64

  • The graphs of those polynomials about x equals 2 and f open parentheses x close parentheses equals ln x can be seen in the following diagrams

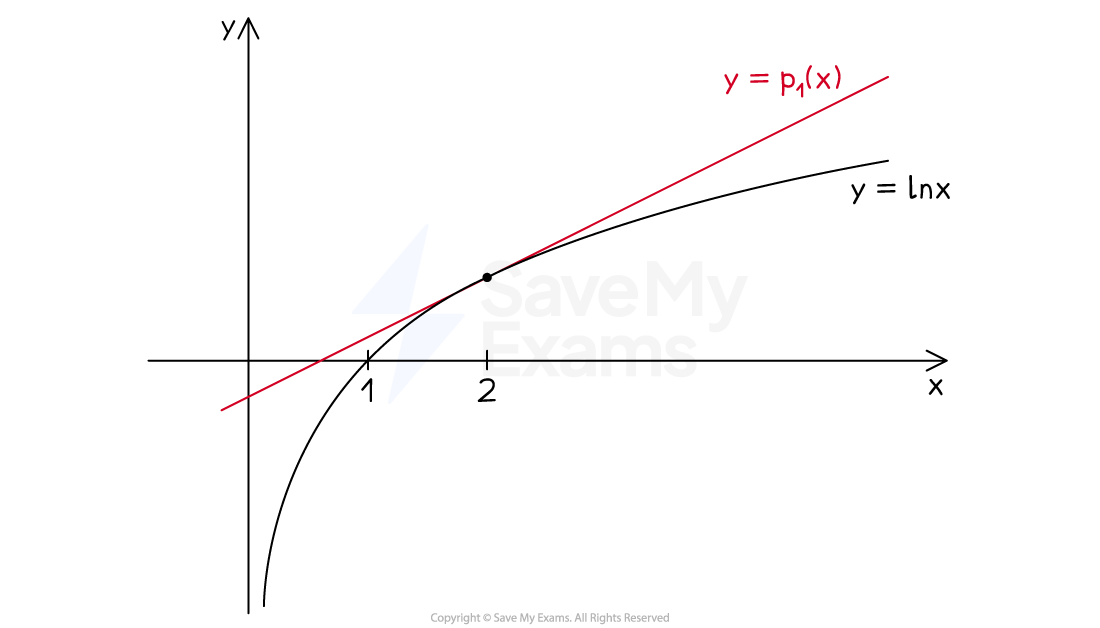
A graph of y=lnx and its first order Taylor approximation at x=2, drawn on the same set of axes
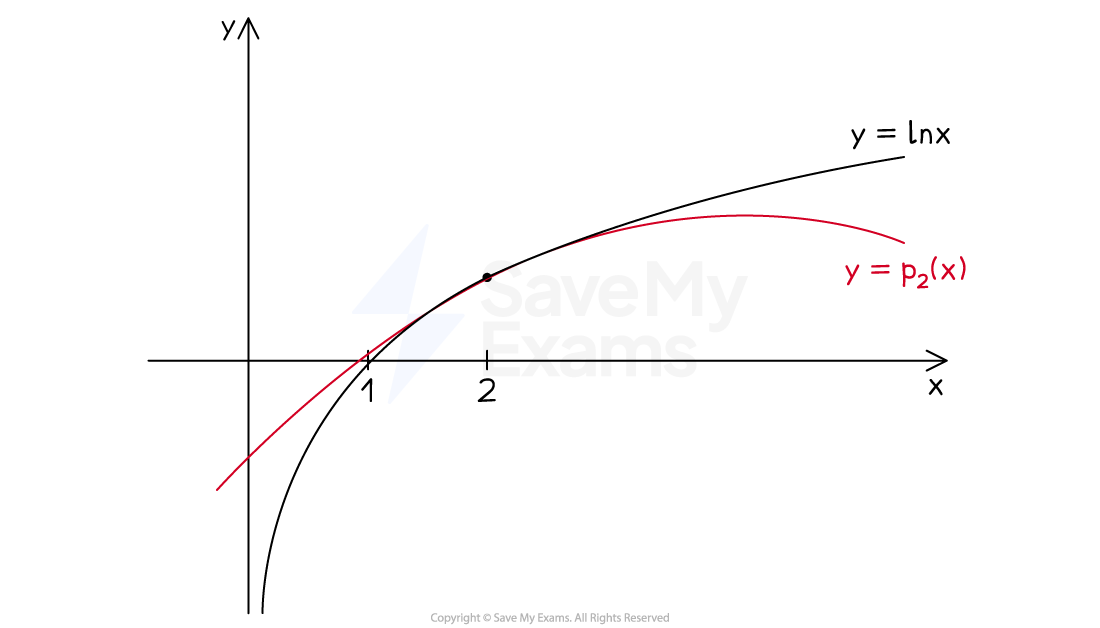
A graph of y=lnx and its second order Taylor approximation at x=2, drawn on the same set of axes
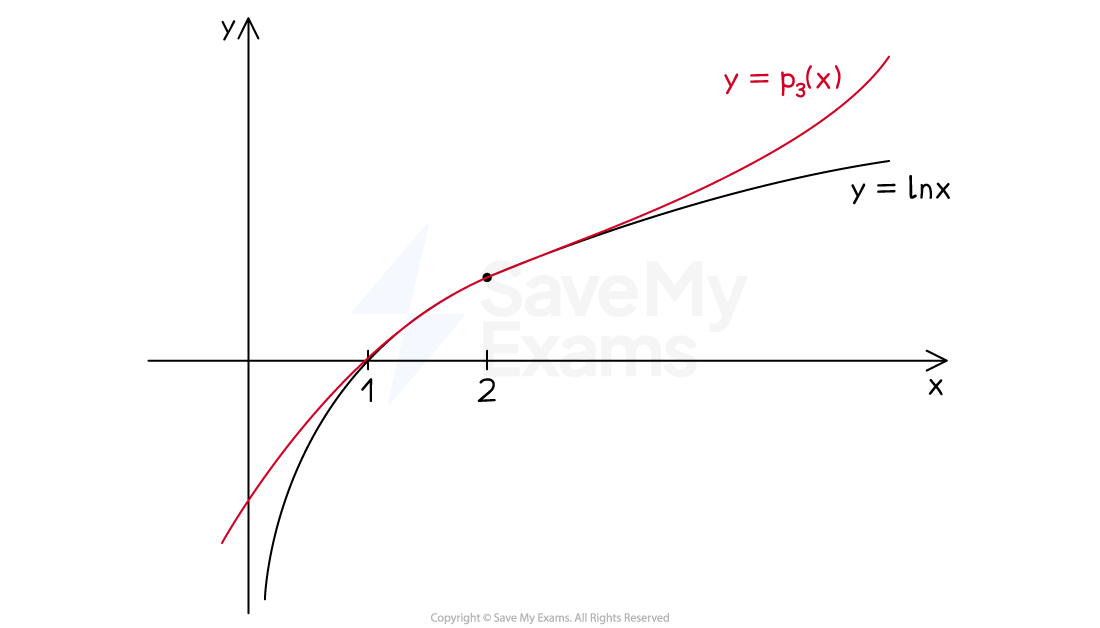
A graph of y=lnx and its third order Taylor approximation at x=2, drawn on the same set of axes
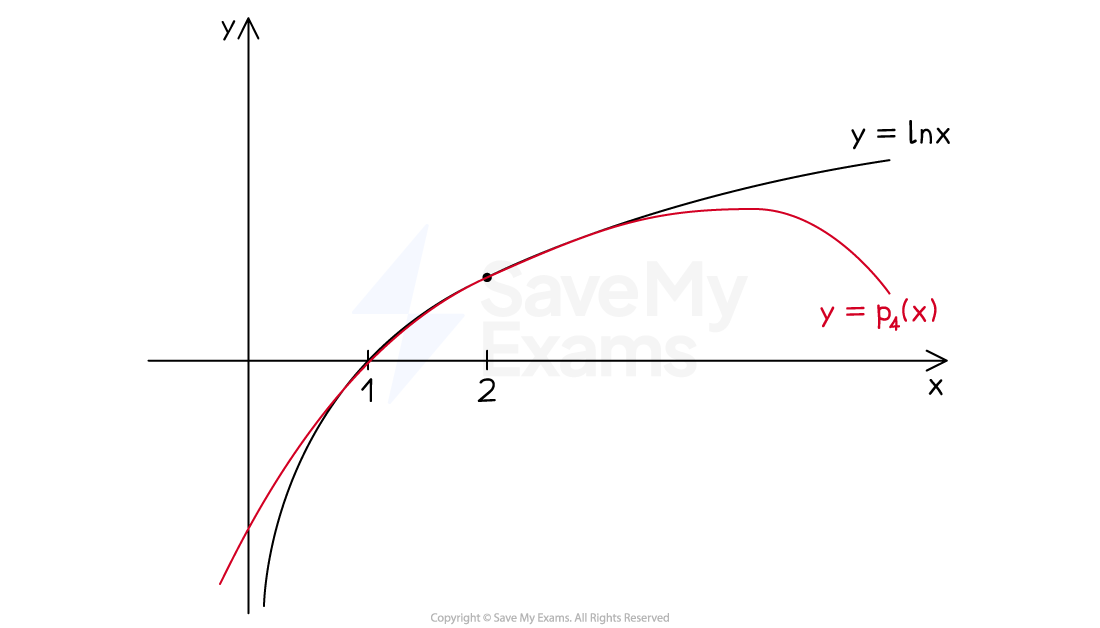
A graph of y=lnx and its fourth order Taylor approximation at x=2, drawn on the same set of axes

  • The diagrams illustrate the following general facts about Taylor polynomials:

    • Their accuracy as an approximation decreases as you move away from x equals a

    • They become a more accurate approximation (and more accurate further away from x equals a) if you increase the degree of the polynomial

      • I.e. adding additional terms in higher powers of x increases the accuracy

What is a Maclaurin polynomial approximation of a function?

  • A Maclaurin polynomial approximation of a function is a special case of a Taylor approximation

  • It is the Taylor approximation of a function about the point x equals 0

    • I.e. if the function f and its first n derivatives all exist at x equals 0, then the nth degree Maclaurin polynomial for f about x equals 0 is

    p subscript n open parentheses x close parentheses equals f open parentheses 0 close parentheses plus f to the power of apostrophe open parentheses 0 close parentheses x plus fraction numerator f to the power of apostrophe apostrophe end exponent open parentheses 0 close parentheses over denominator 2 factorial end fraction x squared plus... plus fraction numerator f to the power of open parentheses n close parentheses end exponent open parentheses 0 close parentheses over denominator n factorial end fraction x to the power of n

Worked Example

(a) Find the Maclaurin polynomial for the function f open parentheses x close parentheses equals e to the power of x up to and including the term in x cubed.

Recall that this is the Taylor approximation about x equals 0

Use p subscript n open parentheses x close parentheses equals f open parentheses 0 close parentheses plus f to the power of apostrophe open parentheses 0 close parentheses x plus fraction numerator f to the power of apostrophe apostrophe end exponent open parentheses 0 close parentheses over denominator 2 factorial end fraction x squared plus... plus fraction numerator f to the power of open parentheses n close parentheses end exponent open parentheses 0 close parentheses over denominator n factorial end fraction x to the power of n

Start by calculating the first three derivatives

f to the power of apostrophe open parentheses x close parentheses equals e to the power of x

f to the power of apostrophe apostrophe end exponent open parentheses x close parentheses equals e to the power of x

f to the power of open parentheses 3 close parentheses end exponent open parentheses x close parentheses equals e to the power of x

Substitute those and x equals 0 into the formula and simplify

table row cell p subscript 3 open parentheses x close parentheses end cell equals cell f open parentheses 0 close parentheses plus f to the power of apostrophe open parentheses 0 close parentheses x plus fraction numerator f to the power of apostrophe apostrophe end exponent open parentheses 0 close parentheses over denominator 2 factorial end fraction x squared plus fraction numerator f to the power of open parentheses 3 close parentheses end exponent open parentheses 0 close parentheses over denominator 3 factorial end fraction x cubed end cell row blank equals cell e to the power of 0 plus e to the power of 0 x plus e to the power of 0 over 2 x squared plus e to the power of 0 over 6 x cubed end cell row blank equals cell 1 plus x plus 1 half x squared plus 1 over 6 x cubed end cell end table

table row blank blank cell 1 plus x plus 1 half x squared plus 1 over 6 x cubed end cell end table

(b) Find the Taylor polynomial for the function g open parentheses x close parentheses equals sin x about x equals pi over 3, up to and including the term in x cubed.

Use space p subscript n open parentheses x close parentheses equals f open parentheses a close parentheses plus f to the power of apostrophe open parentheses a close parentheses open parentheses x minus a close parentheses plus fraction numerator f to the power of apostrophe apostrophe end exponent open parentheses a close parentheses over denominator 2 factorial end fraction open parentheses x minus a close parentheses squared plus... plus fraction numerator f to the power of open parentheses n close parentheses end exponent open parentheses a close parentheses over denominator n factorial end fraction open parentheses x minus a close parentheses to the power of n

Start by calculating the first three derivatives of the function g open parentheses x close parentheses equals sin x

g to the power of apostrophe open parentheses x close parentheses equals cos x

g to the power of apostrophe apostrophe end exponent open parentheses x close parentheses equals negative sin x

g to the power of open parentheses 3 close parentheses end exponent open parentheses x close parentheses equals negative cos x

Substitute those and x equals pi over 3 into the formula and simplify

table row cell space p subscript 3 open parentheses x close parentheses end cell equals cell g open parentheses pi over 3 close parentheses plus g to the power of apostrophe open parentheses pi over 3 close parentheses open parentheses x minus pi over 3 close parentheses plus fraction numerator g to the power of apostrophe apostrophe end exponent open parentheses pi over 3 close parentheses over denominator 2 factorial end fraction open parentheses x minus pi over 3 close parentheses squared plus fraction numerator g to the power of open parentheses 3 close parentheses end exponent open parentheses pi over 3 close parentheses over denominator 3 factorial end fraction open parentheses x minus pi over 3 close parentheses cubed end cell row blank equals cell sin open parentheses pi over 3 close parentheses plus cos open parentheses pi over 3 close parentheses open parentheses x minus pi over 3 close parentheses plus fraction numerator negative sin open parentheses pi over 3 close parentheses over denominator 2 end fraction open parentheses x minus pi over 3 close parentheses squared plus fraction numerator negative cos open parentheses pi over 3 close parentheses over denominator 6 end fraction open parentheses x minus pi over 3 close parentheses cubed end cell row blank equals cell fraction numerator square root of 3 over denominator 2 end fraction plus 1 half open parentheses x minus pi over 3 close parentheses plus fraction numerator bevelled fraction numerator negative square root of 3 over denominator 2 end fraction over denominator 2 end fraction open parentheses x minus pi over 3 close parentheses squared plus fraction numerator bevelled fraction numerator negative 1 over denominator 2 end fraction over denominator 6 end fraction open parentheses x minus pi over 3 close parentheses cubed end cell row blank equals cell fraction numerator square root of 3 over denominator 2 end fraction plus 1 half open parentheses x minus pi over 3 close parentheses minus fraction numerator square root of 3 over denominator 4 end fraction open parentheses x minus pi over 3 close parentheses squared minus fraction numerator 1 over denominator 12 end fraction open parentheses x minus pi over 3 close parentheses cubed end cell end table

table row blank blank cell fraction numerator square root of 3 over denominator 2 end fraction plus 1 half open parentheses x minus pi over 3 close parentheses minus fraction numerator square root of 3 over denominator 4 end fraction open parentheses x minus pi over 3 close parentheses squared minus fraction numerator 1 over denominator 12 end fraction open parentheses x minus pi over 3 close parentheses cubed end cell end table

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Alternating Series Error BoundNext:Radius & Interval of Convergence of Power Series
    Author
    Reviewer
    Roger B

    Author: Roger B

    Expertise: Maths

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

    Mark Curtis

    Author: Mark Curtis

    Expertise: Maths

    Mark graduated twice from the University of Oxford: once in 2009 with a First in Mathematics, then again in 2013 with a PhD (DPhil) in Mathematics. He has had nine successful years as a secondary school teacher, specialising in A-Level Further Maths and running extension classes for Oxbridge Maths applicants. Alongside his teaching, he has written five internal textbooks, introduced new spiralling school curriculums and trained other Maths teachers through outreach programmes.