Squeeze Theorem & Trigonometric Limits (College Board AP® Calculus BC) : Study Guide
Squeeze theorem
What is the squeeze theorem?
The squeeze theorem lets you determine limits for a function that is bounded above and below by two other functions
If the two bounding functions have the same limit for some x-value,
then the bounded function must also have the same limit at that x-value
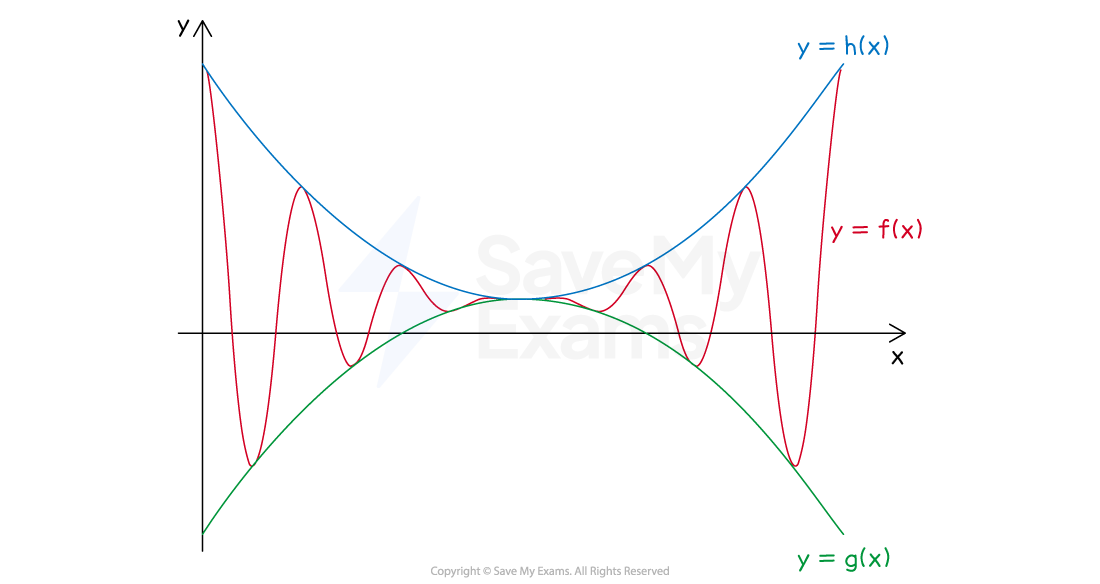
The squeeze theorem
Let
,
and
be functions defined on an open interval including
such that
for all
in the interval (except possibly
), and
Then
Worked Example
Let and
be the functions defined by
and
. It is known that
for
.
Let be a function such that
for
.
Find , being sure to justify your answer.
Answer:
First find the limits for and
They are continuous in an open interval containing 3, so you can use substitution
Those are equal, so along with all the other given info this means you can use the squeeze theorem
Be sure to justify your answer by mentioning the squeeze theorem
By the squeeze theorem, .
Trigonometric limits
What trigonometric limit theorems should I know?
You should know and be able to use the following two trigonometric limit theorems:
These can be combined with properties of limits and/or algebraic manipulation to find other limits
Don't forget the trigonometric identity
Which can be rearranged to give
or
Examiner Tips and Tricks
You can use your graphing calculator to check any limit results that you work out analytically.
Worked Example
Find each of the following limits:
(a)
Answer:
Substitution would give , so instead start with algebraic manipulation
Now use properties of limits along with trigonometric limit theorems
We can make use of the result
(b)
Answer:
Substitution would give , so instead start with algebraic manipulation
Now use properties of limits along with trigonometric limit theorems
We can make use of the result
(c)
Answer:
Substitution would give , so instead start with algebraic manipulation
We can make use of the identity
Now use properties of limits along with trigonometric limit theorems
We can make use of the results

You've read 0 of your 5 free study guides this week
Unlock more, it's free!
Did this page help you?

