Infinite Limits & Limits at Infinity (College Board AP® Calculus BC) : Study Guide
Infinite limits
What do we mean by an infinite limit?
Sometimes the values of a function become unbounded (in the positive or negative direction) as x approaches a certain value
In such cases we talk about the function having an infinite limit at that value of x
For functions defined as fractions or quotients, this happens when the denominator becomes 0 for some value(s) of x
If the value of a function f increases without bound as x approaches some value c, then we write
.
For example,
If the value of a function f decreases without bound as x approaches some value c, then we write
.
For example,
It is possible for the one-sided limits to be different
For example,
But
How about limits that look like 0/∞ or ∞/0?
Sometimes substitution can give limits that look like
or
In the first case the limit will just be equal to zero
For example
As
approaches zero through the positive numbers
and
is a smaller and smaller positive number
and
is a bigger and bigger (i.e. more and more negative) negative number
So near
'from the right',
is negative and getting closer and closer to zero
Therefore
In the second case the limit will diverge to either
or
depending on the behavior near the limit point
For example
As
approaches zero through the positive numbers
and
is a bigger and bigger (i.e. more and more negative) negative number
and
is a smaller and smaller positive number
So near
'from the right',
is negative and getting more and more negative (i.e. bigger and bigger in the negative direction)
Therefore
What is the connection between infinite limits and vertical asymptotes?
When a function has an infinite limit at a point, its graph has a vertical asymptote at that value of x
This is a vertical line that the graph gets closer and closer to (but never touches or intersects) as x approaches that value
Vertical asymptotes on the graph of a function are an indication that it has an infinite limit at that x value
Conversely, identifying infinite limits for a function lets you identify where the graph of the function has vertical asymptotes
Worked Example
The figure below shows the graph of the function defined by
. The dashed line is a vertical asymptote of the graph.
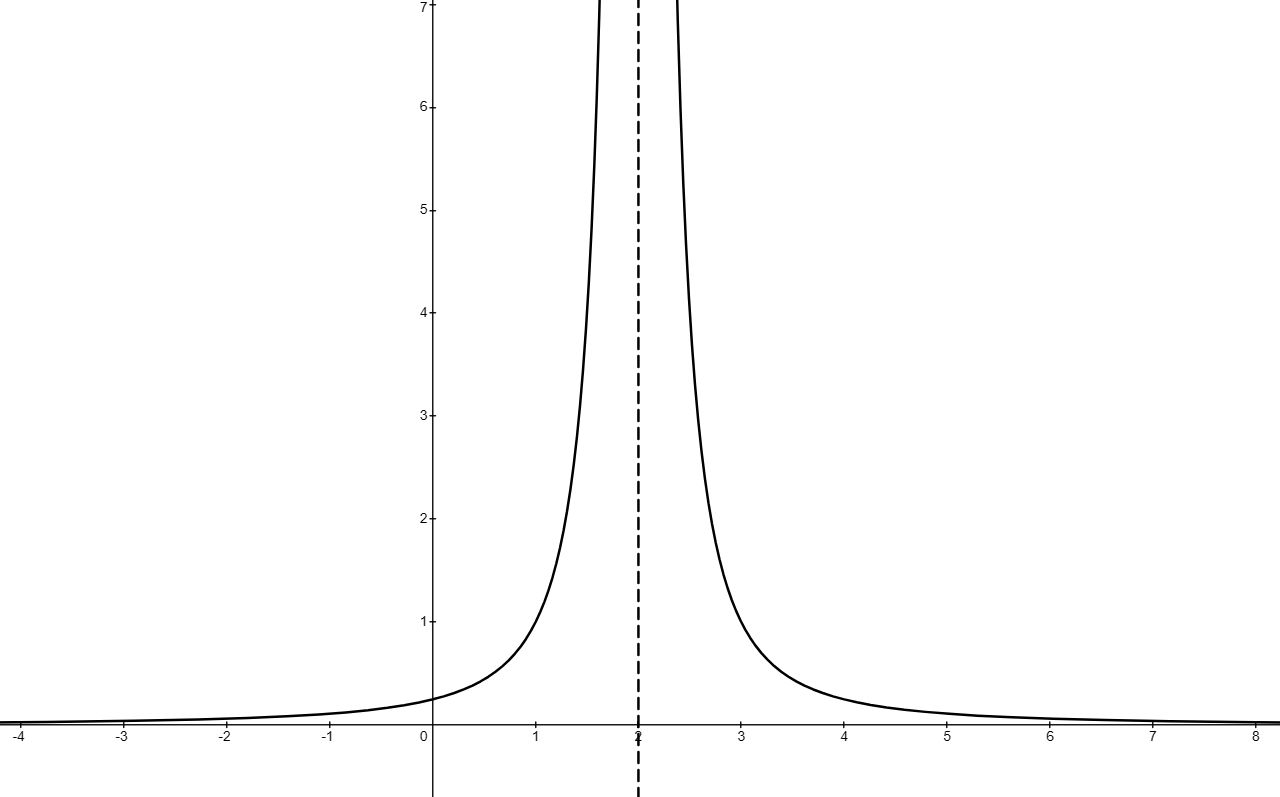
What is ?
Answer:
f(x) is positive for all values of x except 2
As x approaches 2, the denominator gets closer and closer to zero, and the value of the function increases without bound (i.e. gets bigger and bigger in the positive direction)
Limits at infinity
What do we mean by a limit at infinity?
Sometimes we are interested in the value of a function as x increases or decreases without bound
In such cases we talk about the limit at (positive or negative) infinity of the function
When considering the behavior of a function f as x increases without bound (i.e. becomes infinitely big in the positive direction) we write
When considering the behavior of a function f as x decreases without bound (i.e. becomes infinitely big in the negative direction) we write
For some functions, their values as x approaches positive or negative infinity also become unbounded
For example,
and
But for other functions, their values settle down towards (but never quite reach) a fixed value
For example,
and
Because
gets closer and closer to zero as x becomes in large in either the positive or negative directions
What is the connection between limits at infinity and horizontal asymptotes?
When a function has a finite limit at infinity, its graph has a horizontal asymptote at that value of y
This is a horizontal line that the graph gets closer and closer to (but in general never touches or intersects) as x becomes unbounded in the indicated direction
For example if
, then the graph of f will have a horizontal asymptote at y=3
The graph becomes 'more and more like' the asymptote as x becomes unbounded
Horizontal asymptotes on the graph of a function are an indication that the function has a finite limit at infinity
Conversely, identifying finite limits at infinity for a function lets you identify where the graph of the function has horizontal asymptotes
Examiner Tips and Tricks
If an exam question is using a function to model a real-world scenario, be sure to interpret any limits at infinity in the context of the question.
Worked Example
The figure below shows the graph of the function defined by
.
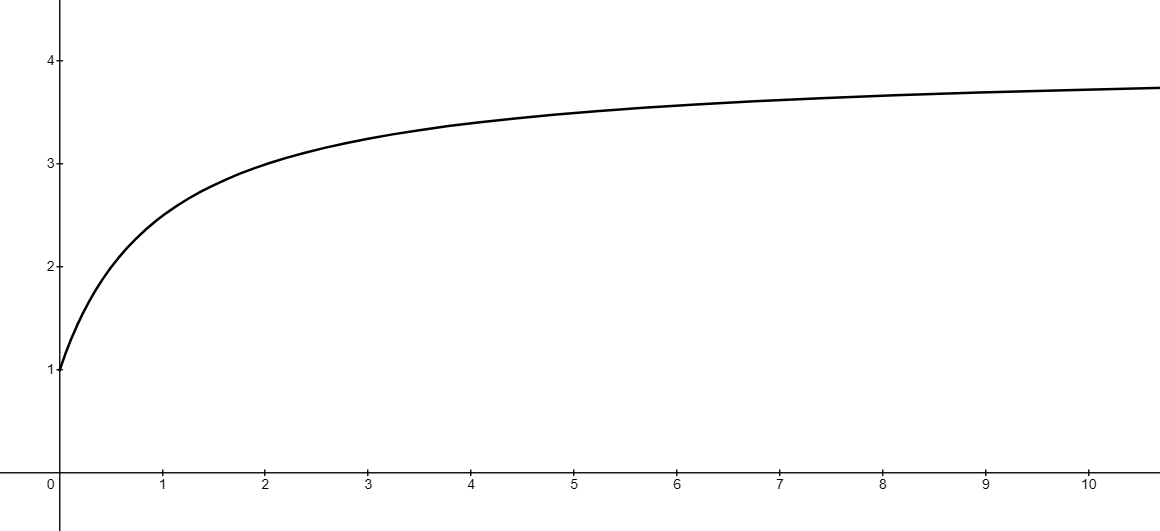
is being used to model the population (in hundreds) of squirrels in a particular area of woodland at time
years after the beginning of a study.
(a) Find .
Answer:
As t gets bigger and bigger in the positive direction, the fraction will become closer and closer to zero
Therefore the function will get closer and closer to 4 (without ever quite reaching 4)
(b) Interpret your answer for part (a) in the context of this problem.
Answer:
Connect the limit in part (a) to the context given in the question
Over time the population of squirrels in the woodland will approach 400.

You've read 0 of your 5 free study guides this week
Sign up now. It’s free!
Did this page help you?

