Properties of Definite Integrals (College Board AP® Calculus BC): Study Guide
Definite integrals
What is a definite integral?
A definite integral is written in the form
is the function being integrated (also known as the integrand)
indicates that the function is being integrated with respect to
and
are the integration limits
the function is integrated 'from
to
'
You'll most often see definite integrals with
But integrals with
are also valid
A definite integral can be interpreted in a number of ways
It is a mathematical operation that outputs a number
based on
and the values of
and
If
is interpreted as a rate of change function
then the definite integral is the accumulation of change as
goes from
to
On the graph of
, where
on the interval
the definite integral gives the area between
and the
-axis, between
and
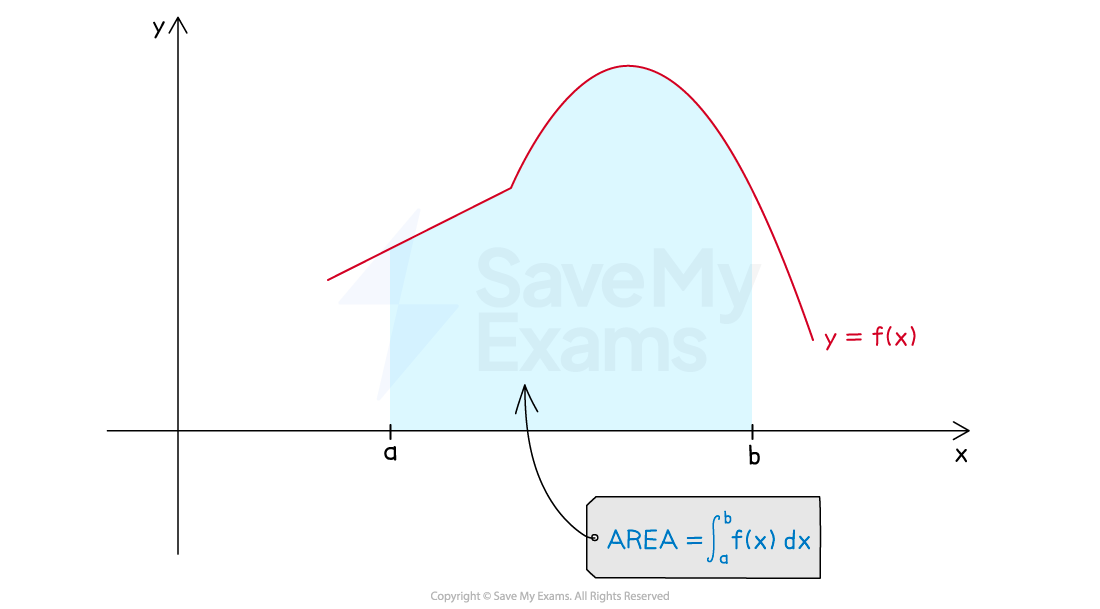
How is a definite integral defined as a limit of Riemann sums?
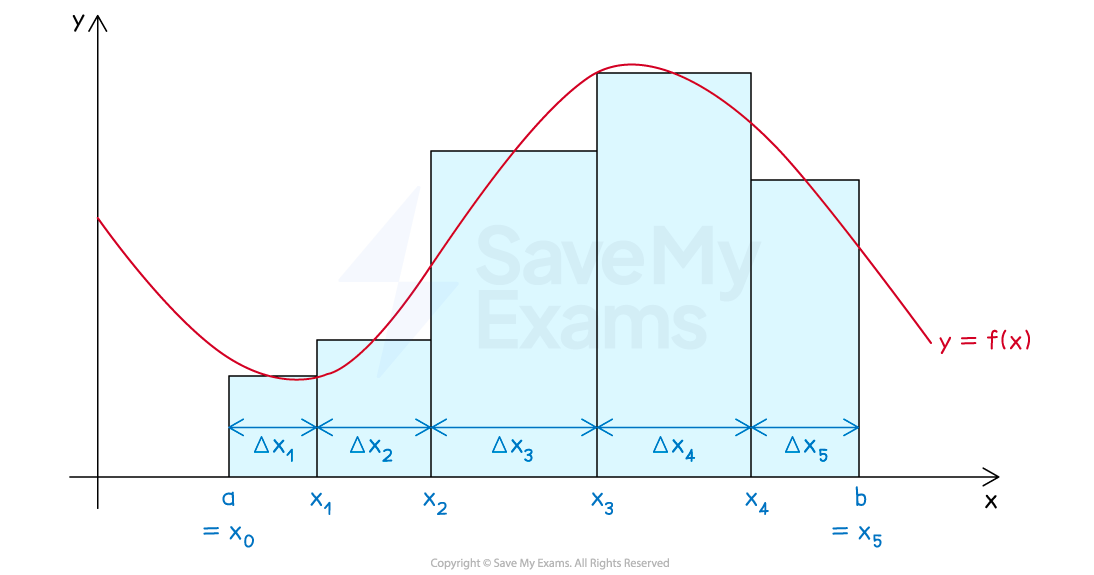
The value of a definite integral can be defined as a limit of Riemann sums:
is the number of subintervals used for the sum
This is the same as the number of rectangles
is a value of
in the
th subinterval
note that this is any value in the
th subinterval
is the width of the
th subinterval
i.e. the width of the
th rectangle
means the limit as the width of the largest subinterval (and hence of all subintervals) approaches zero
As the subintervals (and rectangles) get narrower and narrower
the area of the approximating rectangles gets closer and closer to the exact area under the curve
Note that having the width of the largest subinterval approach zero
is equivalent to having the number of subintervals approach infinity
Therefore the Riemann sum limit for a definite integral can also be written with
as the limit index
If the subintervals are assumed to be of equal width, then expressions for
and
can be written in terms of
,
and
See the Worked Example
Examiner Tips and Tricks
You are not expected to work out the value of a definite integral using the limit of Riemann sums!
See the 'Evaluating Definite Integrals' study guide for the method that is usually used
But you should be able to recognise limit and definite integral expressions that are equivalent
Worked Example
Evaluate the following limit
Answer:
The trick here is recognizing this as a limit of Riemann sums
The key term is
For a Riemann sum with equal subintervals and a total interval width of 5, this is the width of the
th subinterval
I.e.
and
If the total interval starts at -3, then
,
,
, etc.
I.e.
and
This means
can be interpreted as
I.e.
Note that the sum is set up in the form of a right Riemann sum
I.e. with
But as
the type of Riemann sum used becomes insignificant
Recognizing all of this means the limit can be rewritten as a definite integral
The value can be worked out by evaluating the definite integral
Definite Integrals of sums, differences and constant multiples
What are the properties of sums, differences and constant multiples of definite integrals?
These are related to the equivalent properties for indefinite integrals
Definite integral of a constant times a function
If
is a constant, then
I.e. the constant can be brought out in front of the integral as a multiplier
Definite integral of a sum or difference of functions
If
and
are two functions being integrated over the same interval, then
I.e. the integral of a sum (or difference) is equal to the sum (or difference) of integrals
Changing limits of integration
What are the definite integral properties involving integration limits?
There are three properties you should know here
Definite integral of a zero-length interval
For any function
I.e. if the top and bottom integration limits are equal, the definite integral is equal to zero
Reversing the limits of integration
For a function
I.e. reversing the integration limits 'flips' the sign of the value of the definite integral
Definite integrals on adjacent intervals
For a function
, and for
such that
I.e. the sum of definite integrals over adjacent subintervals of
is equal to the total definite integral from
to
Worked Example
is a function such that
and
.
is a function such that
.
Find the value of .
Answer:
First use the sum, difference and constant multiple properties
From the reversing the limits of integration property, we know that and
Use the adjacent intervals property to find
Now we have all the values we need
Worked Example
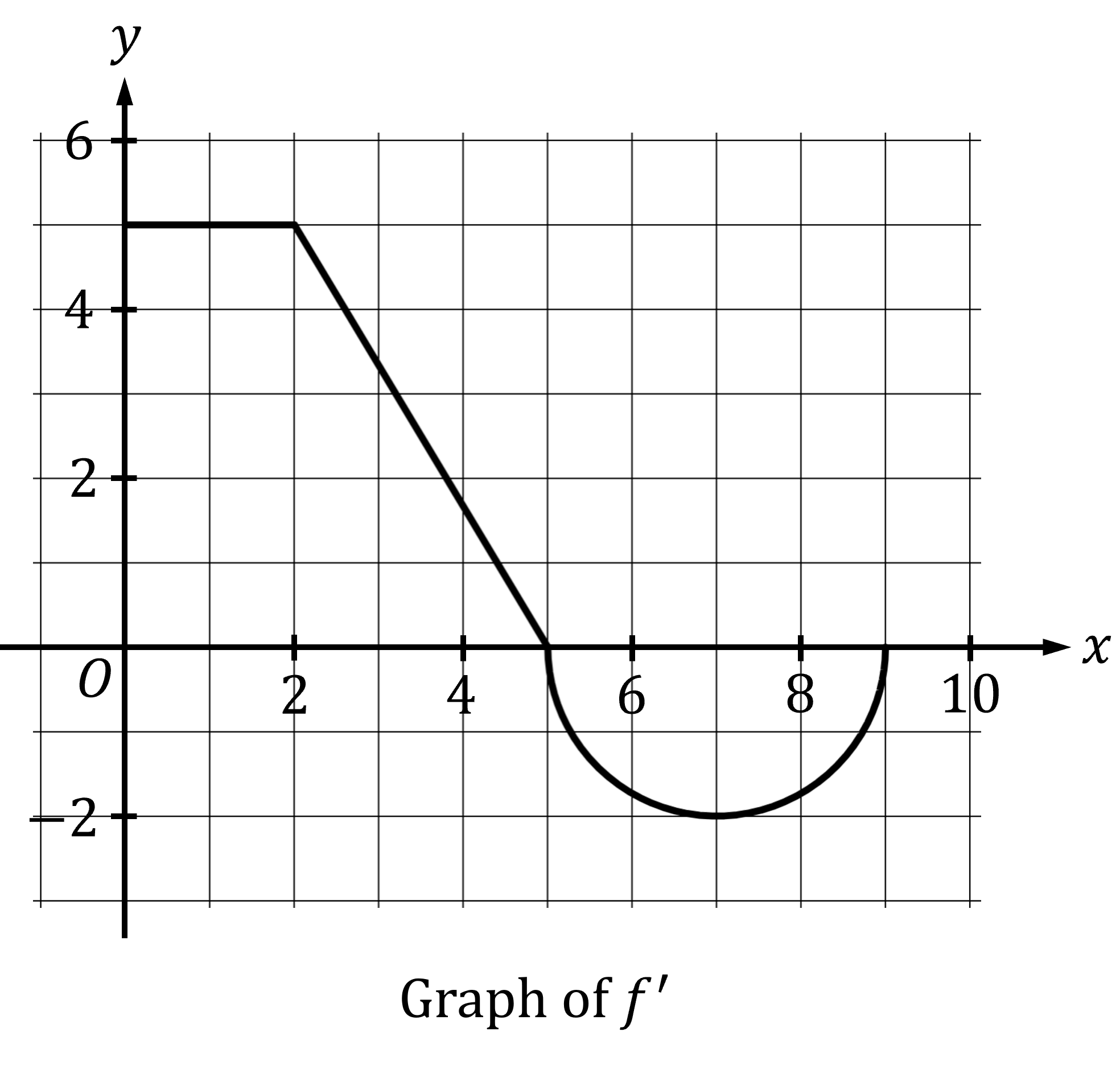
The function is defined on the closed interval
and satisfies
. The graph of
, the derivative of
, consists of two line segments and a semicircle, as shown in the figure.
Find
(a)
Answer:
The value of at 9 will be the value at 5, plus the accumulation of change between 5 and 9
The integral of from 5 to 9 is the area of a semicircle of radius 2; but because
is below the
-axis the value of the definite integral will be negative
(b)
Answer:
The value of at 0 will be the value at 5, plus the accumulation of change between 5 and 0; i.e. going 'backwards' along the
-axis
Use the 'reversing the limits of integration' property
The integral of from 0 to 5 is the area of a rectangle of width 2 and height 5, and a right triangle of base 3 and height 5

Unlock more, it's free!
Did this page help you?