Fundamental Theorem of Calculus (College Board AP® Calculus BC): Study Guide
Fundamental theorem of calculus
What is the fundamental theorem of calculus?
The fundamental theorem of calculus is a key result in the study of calculus
It formalizes the idea that 'integration and differentiation are inverse operations'
and expresses several useful facts that follow on from this basic idea
There are two parts of the fundamental theorem that you should be familiar with and be able to use
The first fundamental theorem of calculus
and the second fundamental theorem of calculus
What is the first fundamental theorem of calculus?
The first fundamental theorem of calculus connects antiderivatives with the value of definite integrals
It provides a simple way to find the value of definite integrals
The first fundamental theorem of calculus
If
is a function that is continuous on the closed interval
and
is an antiderivative of
on
Then
See the 'Evaluating Definite Integrals' study guide for details on how this is used
What is the second fundamental theorem of calculus?
The second fundamental theorem of calculus allows an antiderivative to be expressed in the form of an accumulation function
Recall that an accumulation function is a function of
where the variable
occurs as an integration limit:
E.g.
The second fundamental theorem of calculus
If
is a function that is continuous on an interval containing
Then for values of
in that interval
The function
defined by
is an antiderivative of
and
Examiner Tips and Tricks
Be sure you are familiar with the implications of the second fundamental theorem!
Exam questions will probably not refer explicitly to the theorem, but they will expect you to recognize that:
is an antiderivative of
and especially that
Worked Example
The graph of a differentiable function is shown below.
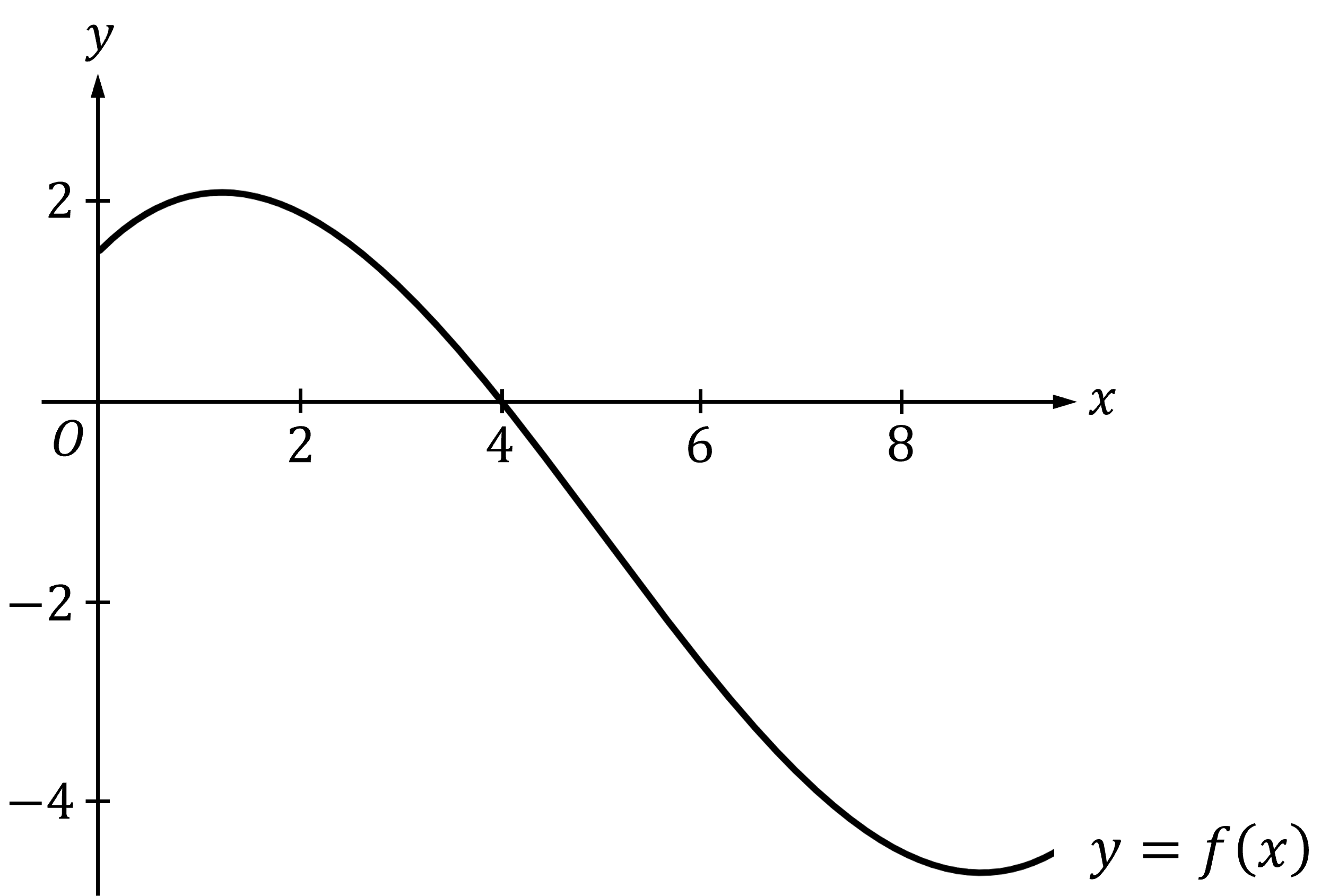
If , which of the following is true?
(A)
(B)
(C)
(D)
(E)
Answer:
We need to see what information we can deduce about ,
and
, which is calculating the accumulated change between 0 and 4
For those values, we can see from the graph that
is positive (i.e. above the
-axis)
So that means that
We are told that
is differentiable
Therefore
is continuous and the second fundamental theorem of calculus is valid
By the second fundamental theorem of calculus,
Therefore
So
, as we can see from the graph
From the graph we can see that
is a decreasing function in the vicinity of 4
Therefore
It follows that
Option (E)

You've read 0 of your 5 free study guides this week
Unlock more, it's free!
Did this page help you?