Integration Using Long Division (College Board AP® Calculus BC): Study Guide
Integration using long division
How do I divide polynomials?
It is possible to use polynomial long division to simplify a rational function like
This can make the function much easier to integrate
Polynomial division works just like the long division method used for regular numbers:

The answer to a polynomial division is built up term by term
working downwards in powers of the variable (usually x)
E.g. dividing
by
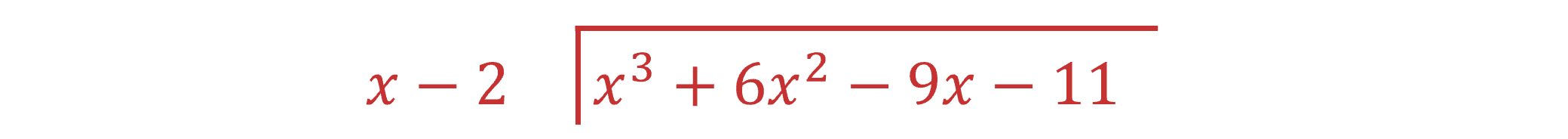
(the thing being divided) is known as the dividend
and
(the thing we're dividing by) is known as the divisor
Start by dealing with the highest power term in the dividend (
)
Compare the highest power term in the divisor (
)
so
put
on top of the division line
and subtract
from the dividend
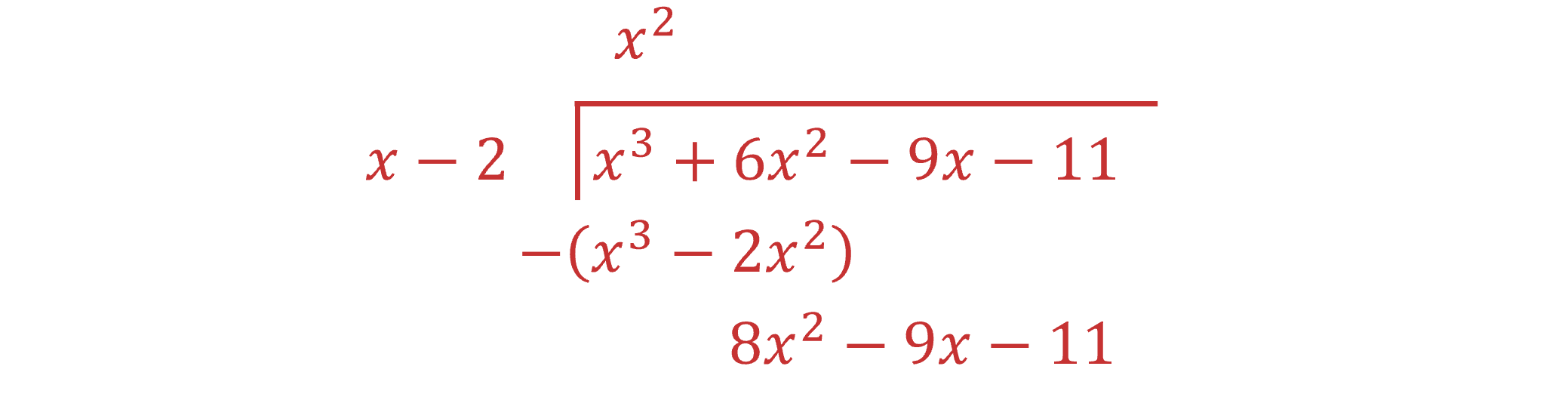
Now deal with the highest power remaining in the expression on the bottom line (
)
Compare the highest power term in the divisor (
)
so
add
on top of the division line
and subtract
from the bottom line
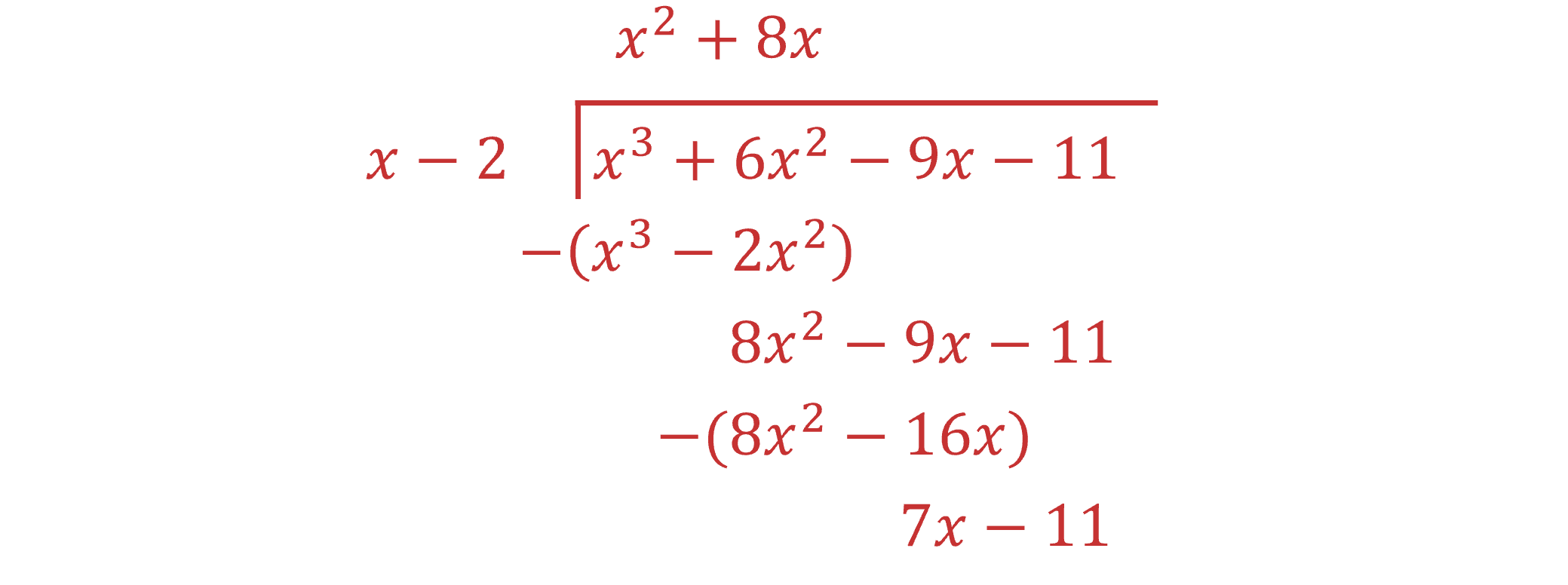
Now deal with the highest power remaining in the expression on the bottom line (
)
Compare the highest power term in the divisor (
)
so
add
on top of the division line
and subtract
from the bottom line
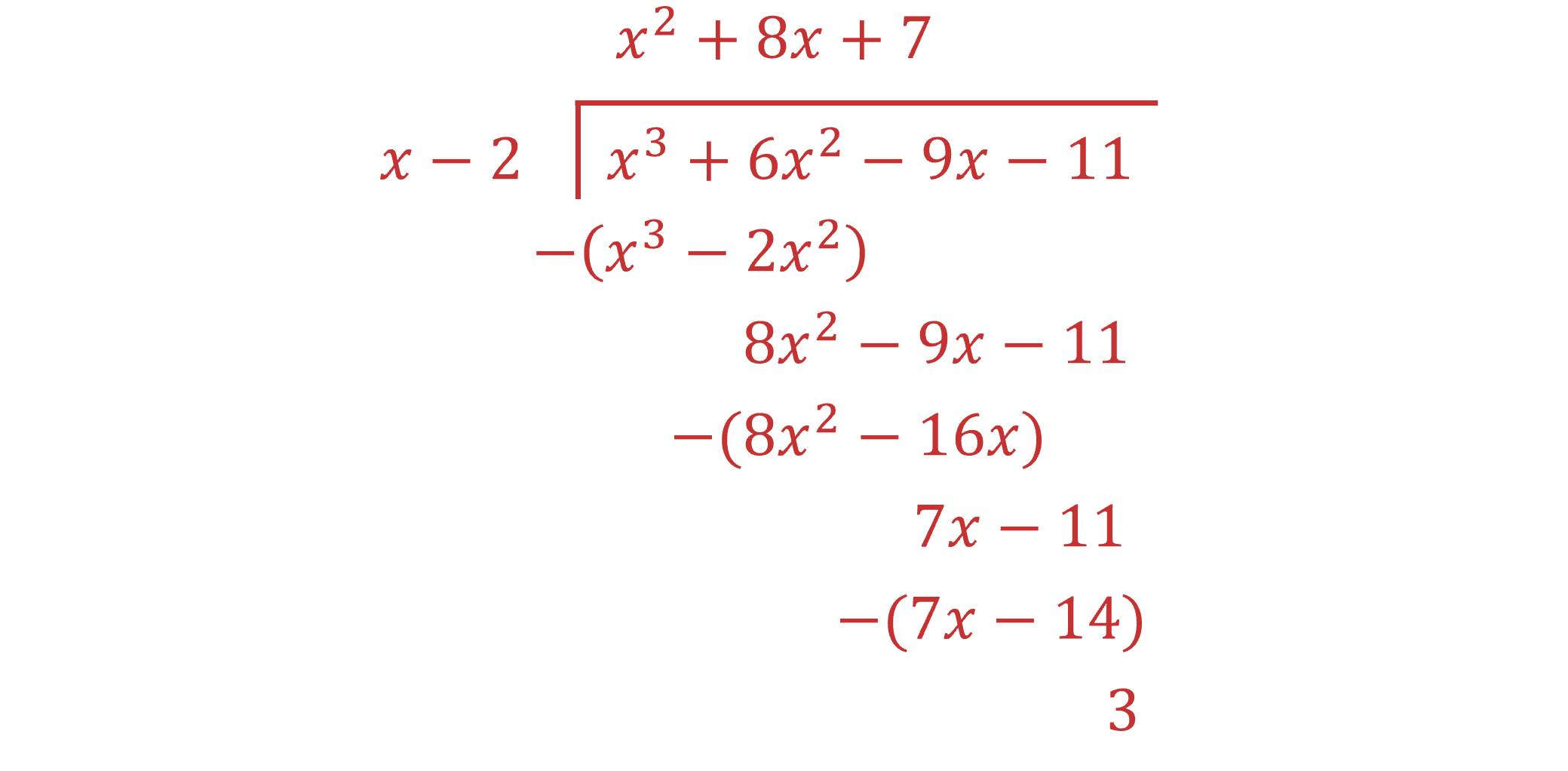
The 3 'left over' at the bottom is the remainder
Therefore
In that new form, the function would be very easy to integrate
Examiner Tips and Tricks
Be extra careful when subtracting expressions with negative coefficients
Using brackets can help you keep track of things
Worked Example
Find the indefinite integral .
Answer:
Start by using polynomial long division to rewrite the function being integrated
Add in to the dividend as a placeholder for the 'missing'
term
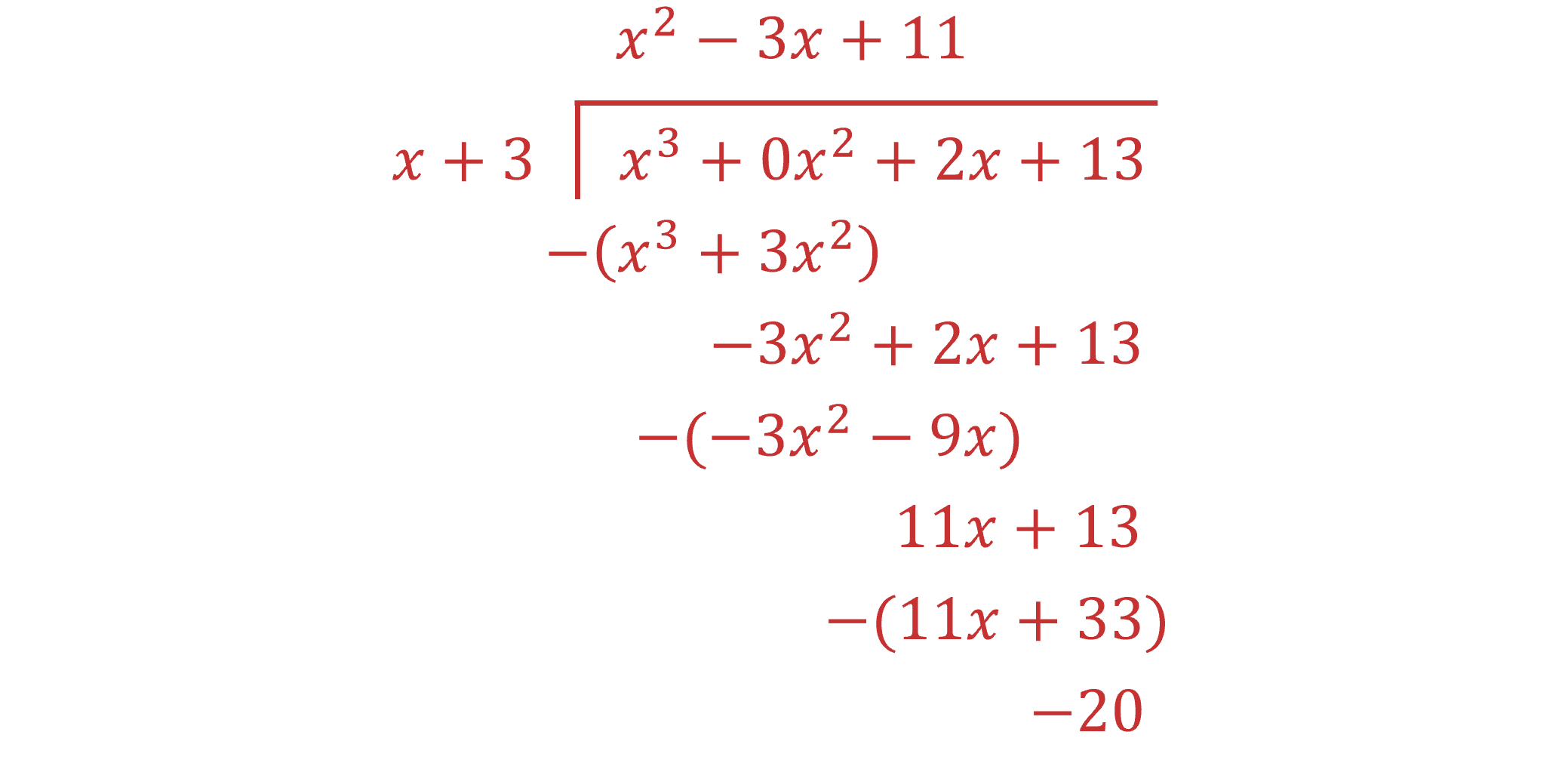
That means , which may be integrated easily

Unlock more, it's free!
Did this page help you?