Study GuidesExam QuestionsPast Papers
AP®MathsCollege BoardCalculus BCStudy GuidesUnit 3: Differentiation of Composite, Implicit & Inverse FunctionsDifferentiation of Composite & Inverse FunctionsThe Inverse Function Theorem

The Inverse Function Theorem (College Board AP® Calculus BC): Study Guide

Jamie Wood

Written by: Jamie Wood

Reviewed by: Dan Finlay

Updated on

College Board Calculus BCCollege Board Calculus AB

The reciprocal of a derivative

What is the reciprocal of a derivative?

  • Derivatives are not fractions, but they behave in the same way as fractions when finding reciprocals

  • The reciprocal of fraction numerator d y over denominator d x end fraction is

    • fraction numerator 1 over denominator open parentheses fraction numerator d y over denominator d x end fraction close parentheses end fraction equals fraction numerator d x over denominator d y end fraction

    • This is only true if fraction numerator d y over denominator d x end fraction not equal to 0

  • Likewise, the reciprocal of fraction numerator d x over denominator d y end fraction is

    • fraction numerator 1 over denominator open parentheses fraction numerator d x over denominator d y end fraction close parentheses end fraction equals fraction numerator d y over denominator d x end fraction

    • This is only true if fraction numerator d x over denominator d y end fraction not equal to 0

  • This property is useful when:

    • Finding the derivative of the inverse of a function

    • Relating rates of change to one another using the chain rule

Derivatives of inverse functions

  • Provided that a function f is:

    • Differentiable

    • A one-to-one function (so that it has an inverse, f to the power of negative 1 end exponent)

  • Its inverse, f to the power of negative 1 end exponent at the point a will be differentiable and the derivative of the inverse at this point will be equal to:

    • open parentheses f to the power of negative 1 end exponent close parentheses to the power of apostrophe open parentheses a close parentheses equals fraction numerator 1 over denominator f to the power of apostrophe open parentheses f to the power of negative 1 end exponent open parentheses a close parentheses close parentheses end fraction

      • This is provided that f apostrophe open parentheses f to the power of negative 1 end exponent open parentheses a close parentheses close parentheses not equal to 0

  • You may also see this written as:

    • g to the power of apostrophe open parentheses a close parentheses equals fraction numerator 1 over denominator f to the power of apostrophe open parentheses g open parentheses a close parentheses close parentheses end fraction

    • Where g open parentheses a close parentheses equals f to the power of negative 1 end exponent open parentheses a close parentheses

      • This is provided that f to the power of apostrophe open parentheses g open parentheses a close parentheses close parentheses not equal to 0

  • This is known as the inverse function theorem

  • To explain why this is true, consider the diagram below

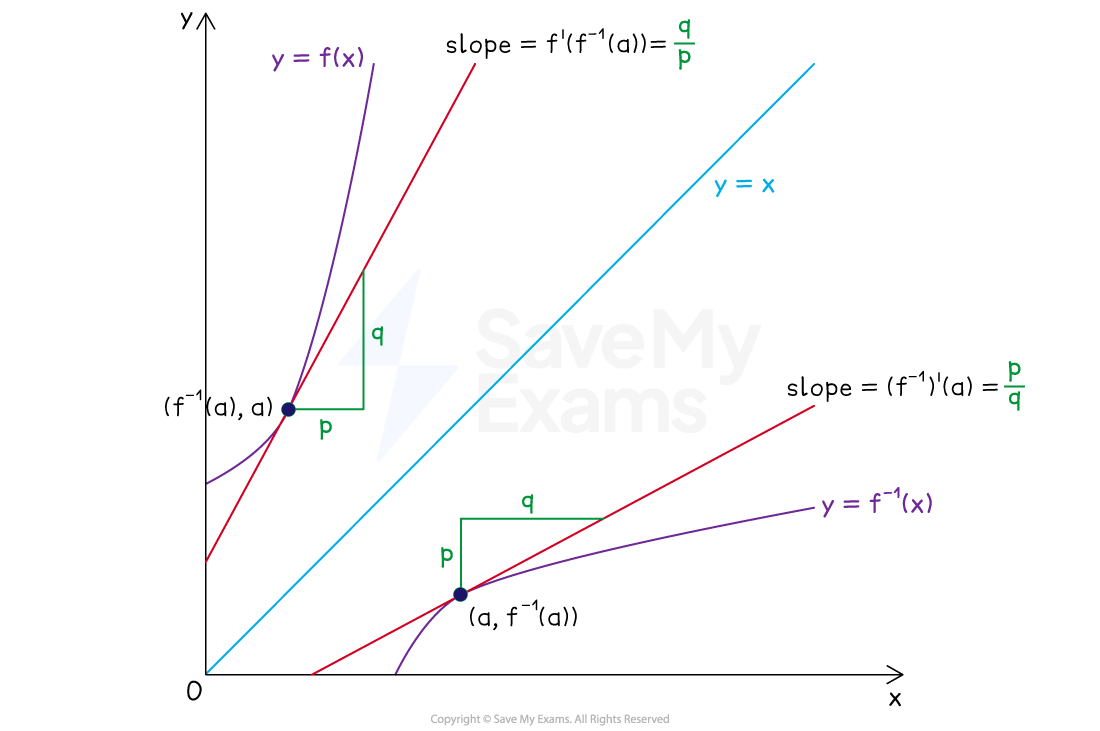
Graphs of a function and its inverse, showing how the tangent to each is related

  • The diagram shows that because the graphs of f open parentheses x close parentheses and f to the power of negative 1 end exponent open parentheses x close parentheses are reflections in the line y equals x:

    • If the slope of f open parentheses x close parentheses at open parentheses f to the power of negative 1 end exponent open parentheses a close parentheses comma space a close parentheses is q over p,

    • then the slope of f to the power of negative 1 end exponent open parentheses x close parentheses at open parentheses a comma space f to the power of negative 1 end exponent open parentheses a close parentheses close parentheses will be p over q

  • This also means that the theorem does not hold if f apostrophe open parentheses f to the power of negative 1 end exponent open parentheses a close parentheses close parentheses equals 0

  • The derivates of these functions at these points are reciprocals of one another,

    • this helps explain why the equation open parentheses f to the power of negative 1 end exponent close parentheses to the power of apostrophe open parentheses a close parentheses equals fraction numerator 1 over denominator f to the power of apostrophe open parentheses f to the power of negative 1 end exponent open parentheses a close parentheses close parentheses end fraction is true

  • If y equals f to the power of negative 1 end exponent open parentheses x close parentheses so that x equals f open parentheses y close parentheses,

    • then the inverse function theorem can be written as fraction numerator d y over denominator d x end fraction equals fraction numerator 1 over denominator open parentheses fraction numerator d x over denominator d y end fraction close parentheses end fraction

    • This form can be more useful for finding an expression for the derivative of the inverse, but it will be in terms of y rather than x

    • The form stated earlier is more useful for finding the derivative of the inverse at a point

How is the inverse function theorem derived?

  • The inverse function theorem can be derived using the definition of an inverse, and the chain rule

  • Let g open parentheses x close parentheses equals f to the power of negative 1 end exponent open parentheses x close parentheses

  • As g open parentheses x close parentheses and f open parentheses x close parentheses are inverses of each other,

    • f open parentheses g open parentheses x close parentheses close parentheses equals x

  • Differentiate both sides with respect to x

    • fraction numerator d over denominator d x end fraction open parentheses f open parentheses g open parentheses x close parentheses close parentheses close parentheses equals fraction numerator d over denominator d x end fraction open parentheses x close parentheses

  • Apply the chain rule to the left hand side, the right hand side differentiates easily

    • f to the power of apostrophe open parentheses g open parentheses x close parentheses close parentheses times g to the power of apostrophe open parentheses x close parentheses equals 1

  • Rearrange

    • g to the power of apostrophe open parentheses x close parentheses equals fraction numerator 1 over denominator f to the power of apostrophe open parentheses g open parentheses x close parentheses close parentheses end fraction

  • Recall that g open parentheses x close parentheses equals f to the power of negative 1 end exponent open parentheses x close parentheses

    • open parentheses f to the power of negative 1 end exponent close parentheses to the power of apostrophe open parentheses x close parentheses equals fraction numerator 1 over denominator f to the power of apostrophe open parentheses f to the power of negative 1 end exponent open parentheses x close parentheses close parentheses end fraction

Worked Example

Let f open parentheses x close parentheses equals open parentheses 3 x plus 4 close parentheses to the power of 4 and let g be the inverse function of f.

Given that f open parentheses 0 close parentheses equals 256, what is the value of g to the power of apostrophe open parentheses 256 close parentheses?

Answer:

Write the inverse function theorem using f open parentheses x close parentheses and f to the power of negative 1 end exponent open parentheses x close parentheses equals g open parentheses x close parentheses

g to the power of apostrophe open parentheses x close parentheses equals fraction numerator 1 over denominator f to the power of apostrophe open parentheses g open parentheses x close parentheses close parentheses end fraction

We are trying to find g to the power of apostrophe open parentheses 256 close parentheses, so fill this in

g to the power of apostrophe open parentheses 256 close parentheses equals fraction numerator 1 over denominator f to the power of apostrophe open parentheses g open parentheses 256 close parentheses close parentheses end fraction

We need to find f to the power of apostrophe open parentheses x close parentheses and g open parentheses 256 close parentheses to be able to calculate the value

Find f to the power of apostrophe open parentheses x close parentheses by differentiating f open parentheses x close parentheses using the chain rule

f to the power of apostrophe open parentheses x close parentheses equals 4 times open parentheses 3 x plus 4 close parentheses cubed times 3 equals 12 open parentheses 3 x plus 4 close parentheses cubed

Using the statement f open parentheses 0 close parentheses equals 256, find the inverse of this

table row cell f open parentheses 0 close parentheses end cell equals 256 row cell f to the power of negative 1 end exponent open parentheses 256 close parentheses end cell equals 0 end table

g open parentheses x close parentheses is the inverse of f open parentheses x close parentheses

g open parentheses 256 close parentheses equals 0

We now have all the information we need, so substitute these in

g to the power of apostrophe open parentheses 256 close parentheses equals fraction numerator 1 over denominator f to the power of apostrophe open parentheses g open parentheses 256 close parentheses close parentheses end fraction equals fraction numerator 1 over denominator f to the power of apostrophe open parentheses 0 close parentheses end fraction equals fraction numerator 1 over denominator 12 open parentheses 3 open parentheses 0 close parentheses plus 4 close parentheses cubed end fraction equals fraction numerator 1 over denominator 12 open parentheses 4 close parentheses cubed end fraction equals 1 over 768

g to the power of apostrophe open parentheses 256 close parentheses equals 1 over 768

Worked Example

The function f is defined by f open parentheses x close parentheses equals x cubed plus 2 x minus 10.

Show that the inverse of f open parentheses x close parentheses exists, and then find the derivative of the inverse of f open parentheses x close parentheses at the point where x equals 125.

Answer:

First check that the inverse exists

f to the power of apostrophe open parentheses x close parentheses equals 3 x squared plus 2, which is always positive

So f open parentheses x close parentheses is always increasing, which means it is a one-to-one function

Therefore f to the power of negative 1 end exponent open parentheses x close parentheses exists

Use the inverse function theorem

open parentheses f to the power of negative 1 end exponent close parentheses to the power of apostrophe open parentheses a close parentheses equals fraction numerator 1 over denominator f to the power of apostrophe open parentheses f to the power of negative 1 end exponent open parentheses a close parentheses close parentheses end fraction

We are trying to find the derivative of the inverse at x equals 125, or open parentheses f to the power of negative 1 end exponent close parentheses to the power of apostrophe open parentheses 125 close parentheses

Fill this in

open parentheses f to the power of negative 1 end exponent close parentheses to the power of apostrophe open parentheses 125 close parentheses equals fraction numerator 1 over denominator f to the power of apostrophe open parentheses f to the power of negative 1 end exponent open parentheses 125 close parentheses close parentheses end fraction

We already know from the first step that f to the power of apostrophe open parentheses x close parentheses equals 3 x squared plus 2

So we just need to find f to the power of negative 1 end exponent open parentheses 125 close parentheses; this is the inverse of f, when x equals 125

To find an equation for the inverse of f, simply switch x and y

f open parentheses x close parentheses equals y equals x cubed plus 2 x minus 10

Inverse: x equals y cubed plus 2 y minus 10

Find the inverse when x equals 125

table row 125 equals cell y cubed plus 2 y minus 10 end cell row 0 equals cell y cubed plus 2 y minus 135 end cell row 5 equals y end table

Fill this in

open parentheses f to the power of negative 1 end exponent close parentheses to the power of apostrophe open parentheses 125 close parentheses equals fraction numerator 1 over denominator f to the power of apostrophe open parentheses f to the power of negative 1 end exponent open parentheses 125 close parentheses close parentheses end fraction equals fraction numerator 1 over denominator f to the power of apostrophe open parentheses 5 close parentheses end fraction equals fraction numerator 1 over denominator 3 open parentheses 5 close parentheses squared plus 2 end fraction equals 1 over 77

open parentheses f to the power of negative 1 end exponent close parentheses to the power of apostrophe open parentheses 125 close parentheses equals 1 over 77

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Did this page help you?

    Previous:The Chain RuleNext:Derivatives of Inverse Trigonometric Functions
    Author
    Reviewer
    Jamie Wood

    Author: Jamie Wood

    Expertise: Maths

    Jamie graduated in 2014 from the University of Bristol with a degree in Electronic and Communications Engineering. He has worked as a teacher for 8 years, in secondary schools and in further education; teaching GCSE and A Level. He is passionate about helping students fulfil their potential through easy-to-use resources and high-quality questions and solutions.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.