Logistic Models (College Board AP® Calculus BC)

Study Guide

Written by: Roger B

Reviewed by: Mark Curtis

Updated on 15 January 2025

Logistic models

What is a logistic model?

The standard logistic growth model is represented by the first-order logistic differential equation
$\frac{d y}{d t} = k y (a - y)$
- $y$ represents the size of a quantity at time $t$
  - Usually this will be the size of a population of some sort
  - This means $y \geq 0$ will always be true
- $k$ is a constant determining the relative rate of change of $y$
  - In general $k > 0$ , with a larger value of $k$ representing a faster rate of change
- $a$ is a constant known as the carrying capacity
  - This is also usually a positive constant
  - It places a limit on the size to which $y$ can grow (if $y$ is increasing) or shrink (if $y$ is decreasing)
  - $y$ will converge to the value $a$ as $t \to \infty$

Examiner Tips and Tricks

The typical statement that leads to a logistic growth model is: “The rate of change of a quantity is jointly proportional to the size of the quantity and the difference between the quantity and the carrying capacity”.

What information can I derive from the logistic differential equation?

Consider different values of $y$ in relation to the equation $\frac{d y}{d t} = k y (a - y)$ with $k, a > 0$ and $y \geq 0$
- If $y = 0$ or $y = a$ then the rate of change $\frac{d y}{d t} = 0$
  - i.e. $y$ is constant and will stay at that value forever
- If $y < a$ , then $\frac{d y}{d t} > 0$
  - i.e. $y$ is increasing (and will continue to increase towards the value of $a$ )
  - This is the most common situation you will see in exam questions
- If $y > a$ , then $\frac{d y}{d t} < 0$
  - i.e. $y$ is decreasing (and will continue to decrease towards the value of $a$ )
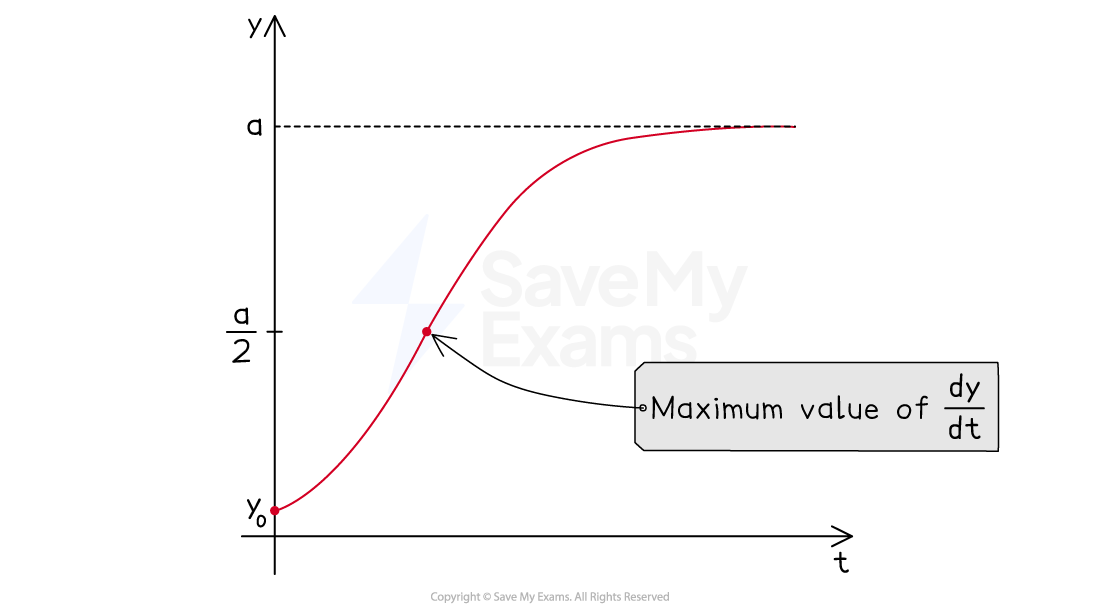
Also note that $k y (a - y) = - k y^{2} + a k y$ is a quadratic function in $y$ with a maximum value when $y = \frac{a}{2}$
- That is when the maximum value of $\frac{d y}{d t}$ occurs
- So for the case where $y < a$ , the value of $y$ will be changing the fastest when $y$ is equal to half the carrying capacity
- If you need to know the time $t$ when that occurs then you will need to solve the logistic equation
  - and then solve for the value of $t$ when $y = \frac{a}{2}$

Examiner Tips and Tricks

Be sure to take account of the context of a question when answering the question or commenting on the model used.

How do I solve a logistic differential equation?

Solving the differential equation uses separation of variables
- It also requires partial fractions to evaluate one of the integrals
Start by separating the variables

$\frac{d y}{d t} = k y (a - y) \Rightarrow \frac{1}{y (a - y)} \frac{d y}{d t} = k \Rightarrow \int \frac{1}{y (a - y)} d y = \int k d t$

Use partial fractions to rewrite the integral on the left
- See the 'Integration Using Partial Fractions' study guide

$\begin{array}{rcl} \frac{1}{a} \int (\frac{1}{y} + \frac{1}{a - y}) d y & = & \int k d t \\ \int (\frac{1}{y} + \frac{1}{a - y}) d y & = & \int a k d t \end{array}$

Integrate both sides of the equation
- Don't forget a constant of integration
- $\frac{1}{a - y}$ can be integrated using the substitution $u = a - y$
  - See the 'Integration Using Substitution' study guide

$\begin{array}{rcl} \ln |y| - \ln |a - y| & = & a k t + C \\ \ln |\frac{y}{a - y}| & = & a k t + C \\ |\frac{y}{a - y}| & = & e^{a k t + C} \end{array}$

As long as $y > 0$ and $y < a$ initially, then $0 < y < a$ will always remain true
- In that case $\frac{y}{a - y} > 0$ , so that $|\frac{y}{a - y}| = \frac{y}{a - y}$

$\frac{y}{a - y} = e^{a k t + C} = e^{C} e^{a k t} = B e^{a k t} (where B = e^{C})$

That can be solved algebraically for $y$ by making $y$ the subject to get

$y = \frac{a B e^{a k t}}{1 + B e^{a k t}}$

If you are given the initial condition that $y = y_{0}$ when $t = 0$ , then you can also work out the value of $B$
- Note that $B$ is just a rewritten form of the constant of integration

$y_{0} = \frac{a B e^{a k (0)}}{1 + B e^{a k (0)}} \Rightarrow y_{0} = \frac{a B}{1 + B} \Rightarrow B = \frac{y_{0}}{a - y_{0}}$

Examiner Tips and Tricks

It is possible to memorize that the logistic equation $\frac{d y}{d t} = k y (a - y)$ , with $a, k > 0$ and $y_{0} = y (0) > 0$ , has the solution

$y = \frac{a B e^{a k t}}{1 + B e^{a k t}}$

where $B = \frac{y_{0}}{a - y_{0}}$ . But for the exam you must also know how to solve differential equations of that form using separation of variables!

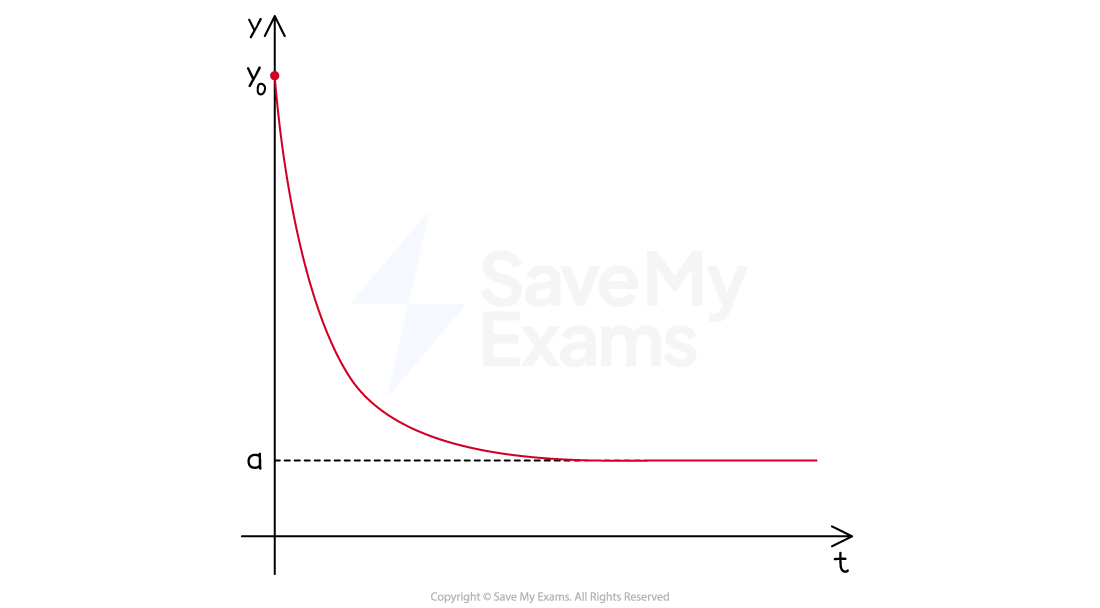
Be careful if $y > a$ initially
- In that case $0 < a < y$ will always remain true
- And $\frac{y}{a - y} < 0$ , so that $|\frac{y}{a - y}| = - \frac{y}{a - y}$
  - The minus sign means the last few steps of the solution will be slightly different
  - However this situation does not usually occur in exam questions

Worked Example

A group of ecologists are studying a population of rabbits on a particular island. The population of rabbits, N, on the island is modelled by the logistic equation

$\frac{d N}{d t} = 0.0012 N (1500 - N)$

where $t$ represents the time in years since the ecologists began their study. At the time the study begins there are 300 rabbits on the island.

(a) Show that the population of rabbits at time $t$ years is given by $N = \frac{1500 e^{1.8 t}}{4 + e^{1.8 t}}$ .

Start by separating the variables

$\begin{array}{rcl} \frac{1}{N (1500 - N)} \frac{d N}{d t} & = & 0.0012 \\ \int \frac{1}{N (1500 - N)} d N & = & \int 0.0012 d t \end{array}$

Rewrite the integral on the left using partial fractions

$\begin{array}{rcl} \frac{1}{1500} \int (\frac{1}{N} + \frac{1}{1500 - N}) d N & = & \int 0.0012 d t \\ \int (\frac{1}{N} + \frac{1}{1500 - N}) d N & = & \int 1.8 d t \end{array}$

Integrate

$\begin{array}{rcl} \ln |N| - \ln |1500 - N| & = & 1.8 t + C \\ \ln |\frac{N}{1500 - N}| & = & 1.8 t + C \\ |\frac{N}{1500 - N}| & = & e^{1.8 t + C} \end{array}$

The initial number of rabbits, $N_{0}$ , is equal to 300

$0 < N_{0} < 1500$ , so the modulus isn't needed in the solution

$\begin{array}{rcl} \frac{N}{1500 - N} & = & e^{1.8 t + C} \end{array}$

Rewrite with $B = e^{C}$

$\begin{array}{rcl} \frac{N}{1500 - N} & = & B e^{1.8 t} \end{array}$

Use $N (0) = 300$ to solve for $B$

$\begin{array}{rcl} \frac{300}{1500 - 300} & = & B e^{1.8 (0)} \\ \frac{1}{4} & = & B e^{0} \\ B & = & \frac{1}{4} \end{array}$

Substitute that value of $B$ into the solution and solve for $N$

$\begin{array}{rcl} \frac{N}{1500 - N} & = & \frac{1}{4} e^{1.8 t} \\ 4 N & = & e^{1.8 t} (1500 - N) \\ N (4 + e^{1.8 t}) & = & 1500 e^{1.8 t} \end{array}$

$\begin{array}{rcl} N & = & \frac{1500 e^{1.8 t}}{4 + e^{1.8 t}} \end{array}$

(b) Find the population of rabbits that the model predicts will be on the island two years after the beginning of the study.

Substitute $t = 2$ into the solution from part (a)

$N (2) = \frac{1500 e^{1.8 (2)}}{4 + e^{1.8 (2)}} = 1352.210 . . .$

Round to the nearest rabbit

1352 rabbits

(c) Determine the maximum size that the model predicts the population of rabbits can grow to. Justify your answer by an appropriate analysis of the equation found in part (a).

From the equation $\frac{d N}{d t} = 0.0012 N (1500 - N)$ , you should be able to tell that the carrying capacity (the maximum possible size of the population) is 1500

You can justify that answer by taking the limit of the solution in part (a) as $t \to \infty$

Start by multiplying by reciprocals to rewrite the solution

$\frac{1500 e^{1.8 t}}{4 + e^{1.8 t}} = \frac{1500 e^{1.8 t}}{4 + e^{1.8 t}} \cdot \frac{e^{- 1.8 t}}{e^{- 1.8 t}} = \frac{1500}{4 e^{- 1.8 t} + 1}$

$4 e^{- 1.8 t} = \frac{4}{e^{1.8 t}}$ , which goes to zero as $t \to \infty$ (because $e^{1.8 t} \to \infty$ as $t \to \infty$ )

$\lim_{t \to \infty} \frac{1500 e^{1.8 t}}{4 + e^{1.8 t}} = \lim_{t \to \infty} \frac{1500}{4 e^{- 1.8 t} + 1} = \frac{1500}{0 + 1} = 1500$

1500 rabbits is the maximum population predicted by the model

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Did this page help you?

Previous:Exponential ModelsNext:Average Value of a Function

Logistic Models (College Board AP® Calculus BC)

Study Guide

Logistic models

What is a logistic model?

What information can I derive from the logistic differential equation?

How do I solve a logistic differential equation?

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

Unit 1: Limits & Continuity

Limits

Definition of a Limit

Infinite Limits & Limits at Infinity

Properties of Limits

Evaluating Limits Analytically

Evaluating Limits Numerically & Graphically

Squeeze Theorem & Trigonometric Limits

Summary of Limits

Selecting Procedures for Determining Limits

Continuity

Continuity

Removable Discontinuities

Non-removable Discontinuities

Intermediate Value Theorem

Unit 2: Differentiation Definition & Fundamental Properties

Definition of Differentiation

Average Rate of Change

Instantaneous Rate of Change

Derivatives & Tangents

Estimating the Derivative at a Point

Differentiability & Continuity

Fundamental Properties of Differentiation

Derivative Rules

Derivatives of Exponentials and Logarithms

Derivatives of Sine and Cosine Functions

The Product Rule

The Quotient Rule

Derivatives of Tangent and Reciprocal Trig Functions

Unit 3: Differentiation of Composite, Implicit & Inverse Functions

Differentiation of Composite & Inverse Functions

The Chain Rule

The Inverse Function Theorem

Derivatives of Inverse Trigonometric Functions

Higher-Order Derivatives

Summary of Differentiation

Selecting Procedures for Calculating Derivatives

Unit 4: Contextual Applications of Differentiation

Rates of Change & Related Rates

Meaning of a Derivative in Context

Motion in a Straight Line

Related Rates

Linearization

Approximating Values of a Function

L'Hospital's Rule

L'Hospital's Rule

Unit 5: Analytical Applications of Differentiation

Graphs of Functions & Their Derivatives

Mean Value Theorem

Extreme Value Theorem

Critical Points

Increasing & Decreasing Functions

First Derivative Test for Local Extrema

Candidates Test for Global Extrema

Concavity of Functions

Second Derivative Test for Local Extrema

Graphs of f, f' & f''

Optimization Problems

Behaviors of Implicit Relations

Second Derivatives of Implicit Functions

Critical Points of Implicit Relations

Unit 6: Integration & Accumulation of Change

Integration & Antiderivatives

Indefinite Integrals

Derivatives & Antiderivatives

Indefinite Integral Rules

Constant of Integration

Riemann Sums & Definite Integrals

Accumulation of Change

Riemann Sums

Trapezoidal sums

Accumulation Functions