Introduction to Differential Equations (College Board AP® Calculus BC) : Study Guide
Modeling with differential equations
What is a differential equation?
A differential equation is simply an equation that contains derivatives
For example
is a differential equation
And so is
It is an equation that includes both variables and rates of change of those variables
What is a first order differential equation?
A first order differential equation is a differential equation that contains first derivatives but no second (or higher) derivatives
For example
is a first order differential equation
But
is not a first order differential equation
because it contains the second derivative
Why are differential equations useful for modeling?
Many quantities of interest in the real world involve rates of change
For example:
The rate of change of a population of animals in a geographic area
The rate of change of the number of people infected by a particular disease
The rate of change of the amount of medication in a person's bloodstream at different times after ingestion
The rate of change of velocity for a falling object
The rate of change of voltage across a component in an electrical circuit
If the relationship between quantities and their rates of change can be written as a differential equation
then solving the equation can allow us to predict the behavior of the quantities in the real world
General and particular solutions to differential equations
What is the difference between general and particular solutions for a differential equation?
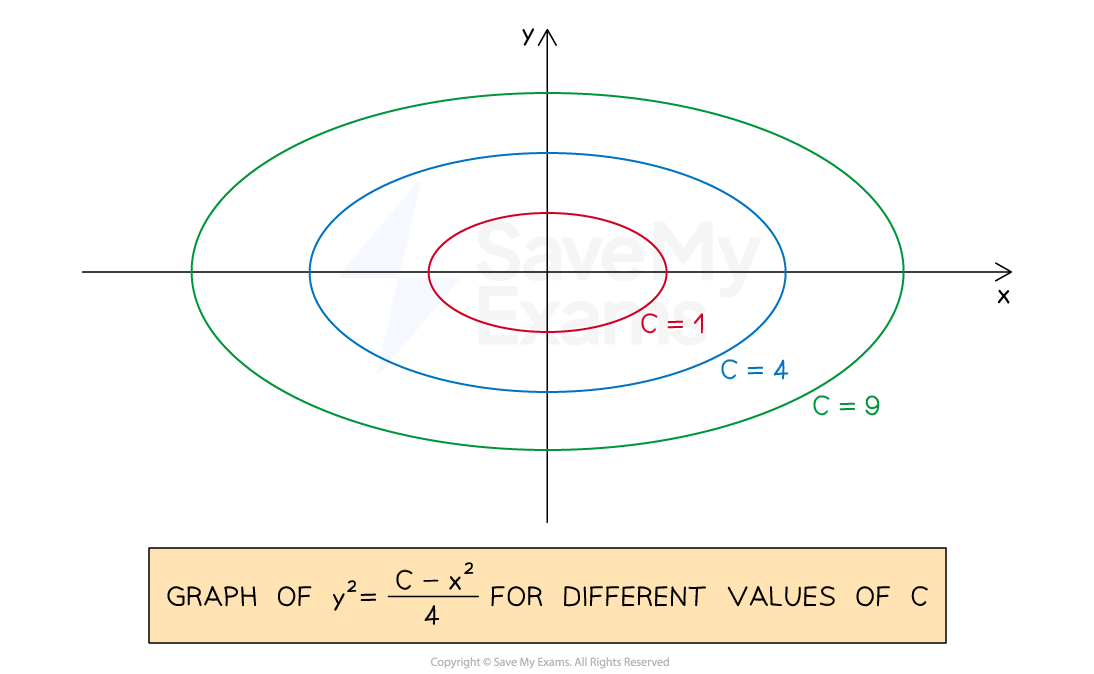
The general solution to a differential equation may be thought of as 'every possible solution' to the differential equation
E.g.
is the general solution to
is an arbitrary constant (like a constant of integration)
The general solution is actually an infinite family of solutions
Each one corresponding to a different value of
The graph of the solution will change depending on the value of
This is shown in the diagram below:
The particular solution to a differential equation is
the specific member of the general family of solutions
that satisfies the equation under a particular set of conditions
E.g. if we know that
when
then
is the only solution that satisfies the differential equation with that set of conditions
A condition like "
when
" is known as an initial condition (or boundary condition)
Finding a particular solution requires knowing an initial condition
Verifying solutions to differential equations
How can I use differentiation to verify solutions for a differential equation?
You can differentiate an answer to a differential equation to verify that it is indeed a solution
E.g. verify that
is a solution to the differential equation
Differentiate the proposed answer with respect to
This matches the original differential equation
So the solution has been verified
For more complicated answers this may require the use of additional techniques
E.g. implicit differentiation and/or substitution
See the Worked Example
Worked Example
Verify that , where
is an arbitrary constant, is a solution to the differential equation
.
Answer:
Start by differentiating both sides of the proposed solution with respect to , using implicit differentiation
Rearrange to make the subject
This may not look like
But remember that
This confirms that is a solution
is a solution to the differential equation

You've read 0 of your 5 free study guides this week
Sign up now. It’s free!
Did this page help you?

