Related Rates (College Board AP® Calculus BC): Study Guide
Solving related rates problems
What are related rates?
Several rates of change can be linked together using the chain rule
The chain rule states that
This can be adapted or extended to other variables depending on the context
How do I solve a related rates problem?
The most important part is forming an equation linking several rates together
Consider:
Which rate are you trying to find?
Which rates do you know?
Which rates could you find (by differentiating)?
Remember that if you know, for example,
, you can easily find
by finding the reciprocal
Once you have formed the equation linking several rates, you should be able to substitute in known values to find an answer
How do I form an equation linking several rates?
Consider which rate you are trying to find
E.g. "The rate of change of volume with respect to time" would be
Consider the rates you know
E.g. you may know the rate of change of height with respect to time,
Consider the rates you can work out by differentiating
E.g. you can work out the rate of change of volume with respect to height,
, using a formula that links volume with height
It can help to list out all the rates
Start with the rate you want to find, and leave blank spaces for rates that may help you find it
Fill in the numerator you are looking for in one of the blank numerators, and do the same for the denominator
Remember that all the terms other than these two, should cancel each other out
This should give you some clues about which rates link together
In this example the related rates equation would be
How can I use implicit differentiation to solve a related rates problem?
An alternative method is to differentiate a known equation with respect to the variable you are interested in
For example if you have the equation
,
and you need to find a rate linked with time, differentiate with respect to time as you would when using implicit differentiation
Then substitute in the information you know to find the desired rate of change
Worked Example
The volume of a particular shape is given by , where
is measured in meters cubed and
is measured in meters.
Given that the rate of change of volume with respect to time is 7 meters cubed per minute, find the exact rate of change of with respect to time in meters per minute, at the time when
is 2 meters.
Answer:
Identify the rate we are trying to find: the rate of change of with respect to
Identify any rates we know
Identify any rates we can work out, and find them
In this case we have a formula for in terms of
, so we can find
Find an equation linking the rates
Start by writing down the rate we are trying to find, and fill in the numerator and denominator on the right hand side
This structure should give you a clue as to how to arrange the other rates
We have , and we have
so we therefore also have
by finding the reciprocal
Fill in the information we know
We are asked to find the rate when , so substitute this in to find the answer
The question asks for the rate as an exact value, so leave it in terms of
meters per minute
An alternative method for this question is starting with the equation for the volume
Differentiate implicitly with respect to instead
And then substitute in the values of and
meters per minute
What else should I be aware of in related rates questions?
The related rates equation may contain more than three terms
E.g.
Just remember that all terms except the numerator and denominator you are looking for will cancel out
Any differentiating you need to do could involve
Chain rule
Product rule or quotient rule
Implicit differentiation
Known results e.g. Trigonometric functions or exponentials
Be careful with which variables are constant, and which are changing in a problem
E.g. If a cone is shrinking, such as when liquid is leaking from a container,
then both the height of the cone, and the radius of the cone will be changing
This means if you had to differentiate
with respect to either
or
,
you would need to use the product rule and implicit differentiation
Drawing a diagram can help
In particular look out for similar shapes
E.g. When a cone shrinks, but retains its cone-shape, the ratio of the radius to the height will remain constant
For a cone of height 20 and radius 5, the ratio of the radius to the height will always be 5:20
So if you know the height after a certain time, you can also work out the radius
Worked Example
A ladder is sliding down a long vertical wall. The ladder is 17 meters long, and the top is slipping down the wall at a rate of 6 meters per second. Find how fast the bottom of the ladder is moving along the ground when the bottom is 15 meters away from the wall.
Answer:
Label the change in height as , and note it will be negative as it is moving downwards
The hypotenuse will always remain as 17, as this is the length of the ladder
The speed at which the bottom of the ladder is moving away from the wall is
Draw a diagram with this information
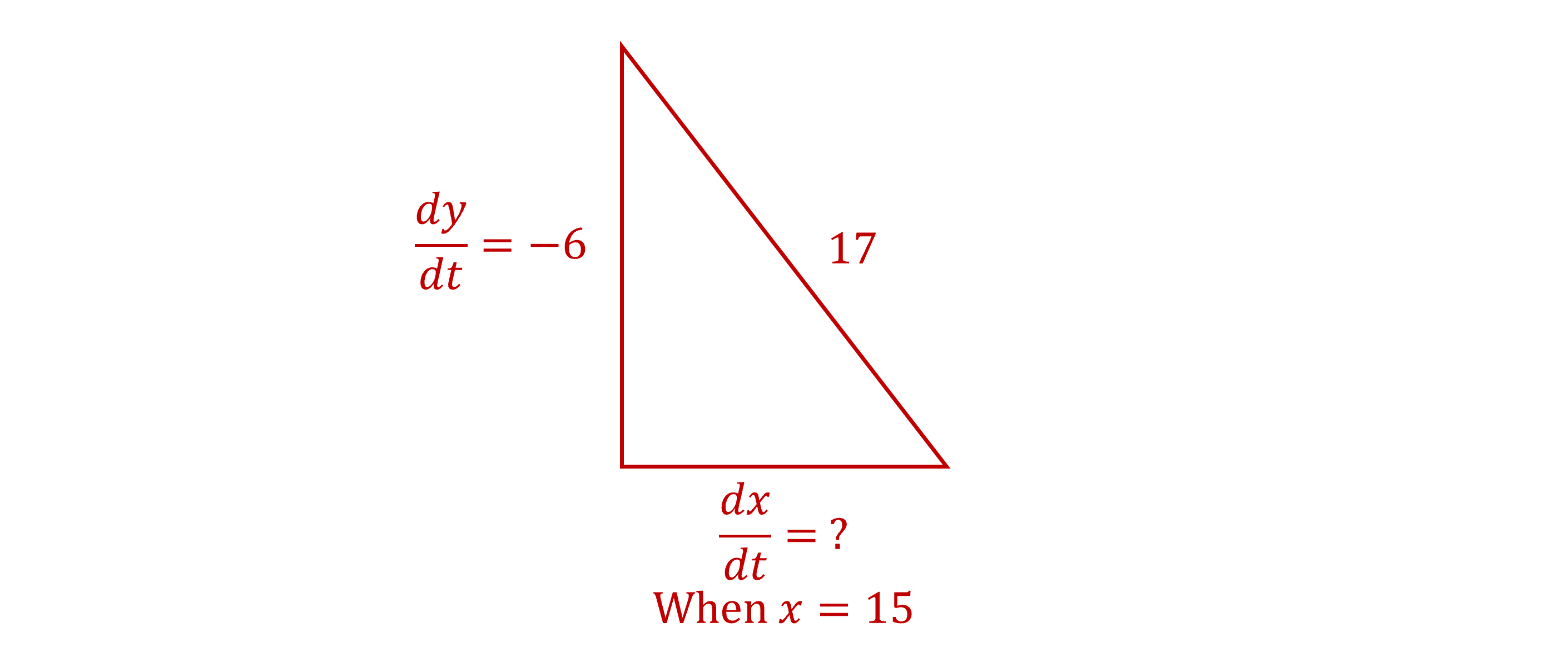
Form an equation for
We already know , so we just need an expression for
An expression linking and
can be found by applying Pythagoras' theorem to the lengths in the diagram, as they form a right-angled triangle
We can differentiate this to find an expression for
Because and
are both variable, implicit differentiation must be used to differentiate each term with respect to
So we can now rewrite the equation linking the rates
We can also use Pythagoras to find when
is 15
When , we now know that
, and we were told in the question that
3.2 metres per second
An alternative method for this question is starting with the equation linking the sides of the ladder
Differentiate implicitly with respect to instead
And then substitute in the values of ,
, and
3.2 metres per second

Unlock more, it's free!
Did this page help you?